11.16~11.19绘制图表，导入EXCEL中数据，进行拟合

这个错误通常是由于传递给curve_fit函数的数据类型不正确引起的。根据你提供的代码和错误信息，有几个可能的原因：

数据类型错误：请确保ce_data、lg_data和product_data是NumPy数组或类似的可迭代对象，且其元素的数据类型为浮点数。你可以使用print(type(ce_data))等语句检查数据类型。
数据维度不匹配：curve_fit函数的第一个参数是要拟合的模型函数，其后的参数应该是要拟合的数据。根据你的代码，模型函数是reaction_model，而数据是(ce_data, lg_data)和product_data。请确保数据的维度匹配，即ce_data、lg_data和product_data具有相同的长度或形状。
数据元素过于复杂：错误信息中的"object too deep for desired array"提示可能是由于数据元素过于复杂而导致的。在使用curve_fit函数之前，确保数据不包含任何复杂对象或嵌套结构。如果数据中包含复杂对象，可以尝试将其转换为简单的数值或处理数据以满足函数的要求。

检查以上可能的原因，并根据需要调整代码和数据类型，以解决这个错误。

绘制图表

fig = plt.figure() 创建一个新的图形窗口。
ax = fig.add_subplot(111, projection='3d') 在图形窗口中添加一个三维子图（子图索引为111），并指定投影方式为3D。
ax.scatter(x1, x2, y, c='b', marker='o') 在三维子图中绘制散点图，其中x1和x2表示两个自变量的值，y表示因变量的值。参数c设置散点的颜色为蓝色（'b'），marker设置散点的形状为圆形（'o'）。

多项式回归

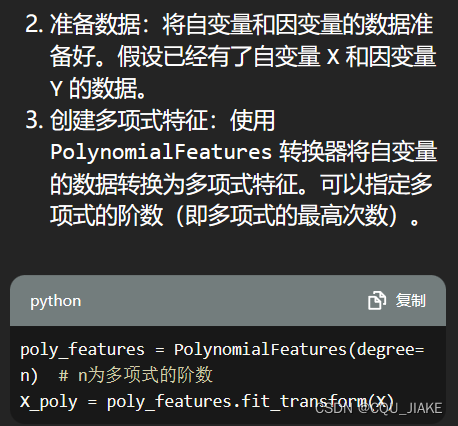
将excel导入进python

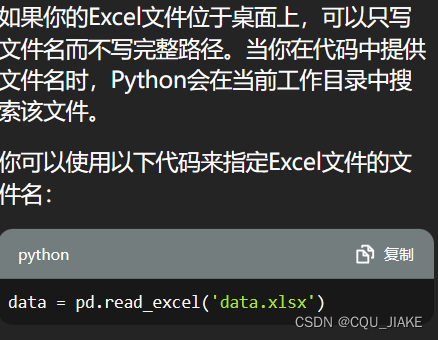
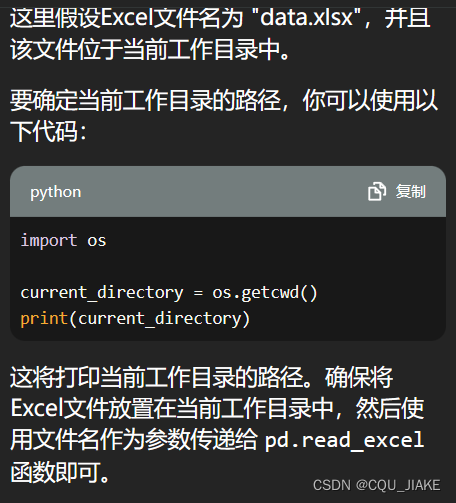
只有excel和py的主文件在同一目录下时才可以只写文件名，不然就必须写地址，即使在桌面上也不可以

data = pd.read_excel('C:/Users/26861/Desktop/Annex I- Pyrolysis Product Yields of Three Pyrolysis Combinations.xlsx')

还有就是地址可以用/，用\可能会出现转义字符

import pandas as pd
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 读取Excel文件
data = pd.read_excel('data.xlsx')

# 提取自变量和因变量数据
X = data['自变量列名'].values.reshape(-1, 1)  # 将自变量数据转换为二维数组
Y = data['因变量列名'].values.reshape(-1, 1)  # 将因变量数据转换为二维数组

# 创建多项式特征
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)

# 拟合模型
model = LinearRegression()
model.fit(X_poly, Y)

# 进行预测
Y_pred = model.predict(X_poly)

# 打印拟合结果
print(Y_pred)

# 可以继续进行可视化等操作...
# 生成一系列连续的自变量值，用于绘制曲线
X_plot = np.linspace(0, 1.2, 100).reshape(-1, 1)
X_plot_poly = poly_features.transform(X_plot)

# 进行预测
Y_pred = model.predict(X_plot_poly)

# 绘制原始数据点
plt.scatter(X, Y, color='blue', label='原始数据')

# 绘制拟合曲线
plt.plot(X_plot, Y_pred, color='red', label='拟合曲线')

# 设置图例和标签
plt.legend()
plt.xlabel('自变量')
plt.ylabel('因变量')
plt.title('多项式回归拟合')

# 显示图形
plt.show()

import pandas as pd
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# 读取Excel文件
data = pd.read_excel('C:/Users/26861/Desktop/Annex I- Pyrolysis Product Yields of Three Pyrolysis Combinations.xlsx')

# 提取自变量和因变量数据
X = data['DFA/CS'].values.reshape(-1, 1)  # 将自变量数据转换为二维数组
Y = data['Tar yield'].values.reshape(-1, 1)  # 将因变量数据转换为二维数组

# 创建多项式特征
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)

# 拟合模型
model = LinearRegression()
model.fit(X_poly, Y)

# 进行预测
Y_pred = model.predict(X_poly)

# 打印拟合结果
print(Y_pred)

# 可以继续进行可视化等操作...
# 生成一系列连续的自变量值，用于绘制曲线
X_plot = np.linspace(0, 1.2, 100).reshape(-1, 1)
X_plot_poly = poly_features.transform(X_plot)

# 进行预测
Y_pred = model.predict(X_plot_poly)

# 绘制原始数据点
plt.scatter(X, Y, color='blue', label='point')

# 绘制拟合曲线
plt.plot(X_plot, Y_pred, color='red', label='curve')

# 设置图例和标签
plt.legend()
plt.xlabel('DFA/CS')
plt.ylabel('Tar yelid')
plt.title('curve')

# 显示图形
plt.show()

在从Excel提取自变量和因变量后，将它们转换为二维数组的原因是为了与某些库和函数的要求相匹配。

许多机器学习和数据分析库（如scikit-learn、NumPy等）通常期望输入数据是二维数组的形式，其中每个样本位于行中，每个特征位于列中。通过将自变量和因变量转换为二维数组，可以将数据结构化并满足库和函数的要求。

对于自变量，如果你只有一个自变量列，你可以使用NumPy的`reshape`函数将其转换为二维数组。假设自变量数组为`X`，你可以使用以下代码转换为二维数组：

```python
import numpy as np
X = np.array(X).reshape(-1, 1)
```

这将将`X`数组从一维数组转换为二维数组，其中样本位于行中，特征位于列中。`-1`参数表示自动推断行数，`1`表示列数为1。

对于因变量，如果你有多个因变量列，你可以将它们合并为一个二维数组。假设因变量数组为`Y1`、`Y2`、`Y3`，你可以使用以下代码将它们合并为一个二维数组：

```python
import numpy as np
Y = np.column_stack((Y1, Y2, Y3))
```

这将使用`column_stack`函数将`Y1`、`Y2`和`Y3`列堆叠在一起，形成一个二维数组，其中每个列对应一个因变量。

通过将自变量和因变量转换为二维数组，你可以更方便地使用各种库和函数进行数据分析、建模和拟合操作。

希望这能解答你的问题！如果还有其他问题，请随时提问。

import pandas as pd
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# 读取Excel文件
data = pd.read_excel('C:/Users/26861/Desktop/Annex I- Pyrolysis Product Yields of Three Pyrolysis Combinations.xlsx')

# 提取自变量和因变量数据
X = data['DFA/CS'].values. Reshape(-1, 1)  # 将自变量数据转换为二维数组
Y1 = data['Tar yield'].values. Reshape(-1, 1)  # 将因变量数据转换为二维数组
Y2 = data['Water yield'].values. Reshape(-1, 1)
Y3 = data['Char yield'].values. Reshape(-1, 1)
Y4 = data['Syngas yield'].values.reshape(-1, 1)
# 创建多项式特征
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)

# 拟合模型
model = LinearRegression()
model.fit(X_poly, Y1)
model.fit(X_poly, Y2)
model.fit(X_poly, Y3)
model.fit(X_poly, Y4)
# 进行预测
Y_pred = model.predict(X_poly)

# 打印拟合结果
print(Y_pred)

# 可以继续进行可视化等操作...
# 生成一系列连续的自变量值，用于绘制曲线
X_plot = np.linspace(0, 1.2, 100).reshape(-1, 1)
X_plot_poly = poly_features.transform(X_plot)

# 进行预测
Y_pred = model.predict(X_plot_poly)

# 绘制原始数据点
plt.scatter(X, Y, color='blue', label='point')

# 绘制拟合曲线
plt.plot(X_plot, Y_pred, color='red', label='curve')

# 设置图例和标签
plt.legend()
plt.xlabel('DFA/CS')
plt.ylabel('Tar yelid')
plt.title('curve')

# 显示图形
plt.show()

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 从Excel文件中读取数据
data = pd.read_excel('C:/Users/26861/Desktop/Annex I- Pyrolysis Product Yields of Three Pyrolysis Combinations.xlsx')

# 提取自变量数据列
x = data['DFA/CS'].values

# 提取多个因变量数据列
y_columns = ['Tar yield', 'Water yield', 'Char yield','Syngas yield']  # 替换为实际的数据列名称

# 自定义拟合函数
def func(x, a, b):
    return a * x + b

# 创建图形窗口和子图
fig, axs = plt.subplots(len(y_columns), 1, figsize=(8, 6), sharex=True)

# 遍历每个因变量数据列
for i, y_column in enumerate(y_columns):
    # 提取因变量数据列
    y = data[y_column].values

    # 执行拟合
    params, _ = curve_fit(func, x, y)

    # 生成拟合曲线
    fit = func(x, *params)

    # 绘制原始数据点和拟合曲线
    axs[i].scatter(x, y, label='Data')
    axs[i].plot(x, fit, label='Fit')

    # 添加图例
    axs[i].legend()

# 设置整体图形的标题和横轴标签
fig.suptitle('Fitted Curves')
plt.xlabel('X')

# 调整子图之间的间距
plt.tight_layout()

# 显示图形
plt.show()

得到EXCEL中，

每个单元格在其所在行中的占比

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 从Excel文件中读取数据
data = pd.read_excel('C:/Users/26861/Desktop/Annex I- Pyrolysis Product Yields of Three Pyrolysis Combinations.xlsx')

# 提取自变量数据列
x = data['DFA/CS'].values

# 提取多个因变量数据列
y_columns = ['Tar yield', 'Water yield', 'Char yield','Syngas yield']  # 替换为实际的数据列名称

# 多项式拟合阶数
degree = 2

# 创建图形窗口和子图
fig, axs = plt.subplots(len(y_columns), 1, figsize=(8, 6), sharex=True)

# 遍历每个因变量数据列
for i, y_column in enumerate(y_columns):
    # 提取因变量数据列
    y = data[y_column].values

    # 执行拟合
    coeffs = np.polyfit(x, y, degree)
    poly = np.poly1d(coeffs)
    fit = poly(x)


    # 绘制原始数据点和拟合曲线
    axs[i].scatter(x, y, label='Data')
    axs[i].plot(x, fit, label='Fit')

    # 添加图例
    axs[i].legend()
 # 输出拟合函数的具体信息
    print(f"Fitted function for {y_column}:")
    print(poly)

# 设置整体图形的标题和横轴标签
fig.suptitle('Fitted Curves')
plt.xlabel('X')

# 调整子图之间的间距
plt.tight_layout()

# 显示图形
plt.show()

import pandas as pd
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

# 自定义指数函数
def exponential_func(x, a, b, c):
    return a * np.exp(b * x) + c

# 从Excel文件中读取数据
df = pd.read_excel('C:/Users/26861/Desktop/Annex I- Pyrolysis Product Yields of Three Pyrolysis Combinations.xlsx')
x_data = df['DFA/CS'].values
y_data = df[['Tar yield', 'Water yield', 'Char yield','Syngas yield']].values.T


print(x_data,y_data)
# 创建子图
fig, axs = plt.subplots(2, 2, figsize=(10, 8))

# 针对每个因变量进行拟合和绘图
for i, ax in enumerate(axs.flat):
    y = y_data[i]  # 当前因变量的数据

    # 进行拟合
    popt, pcov = curve_fit(exponential_func, x_data, y, maxfev=10000)  # 增加maxfev的值

    # 绘制拟合曲线
    x_fit = np.linspace(min(x_data), max(x_data), 100)
    y_fit = exponential_func(x_fit, *popt)
    ax.plot(x_fit, y_fit, label='Fit Curve')

    # 绘制原始数据点
    ax.scatter(x_data, y, label='Data')

    # 显示方程信息
    equation_info = f'y = {popt[0]:.2f} * exp({popt[1]:.2f} * x) + {popt[2]:.2f}'
    ax. Text(2, max(y) / 2, equation_info)

    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_title(f'Fit Curve for Variable {i+1}')
    ax.legend()

# 调整子图布局
plt.tight_layout()

# 显示图表
plt.show()

return a * np.exp(-(x - b)**2 / (2 * c**2)) + d

# 非线性最小二乘拟合
popt, pcov = curve_fit(exponential_func, x_data, y_data, maxfev=100000,p0=(1, -1, 1))

拟合时初始值很重要

curve_fit就是最小二乘拟合

对于单调减的初始值设为-1，开始时增加的，设为1

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

x_data = np.array([0., 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8, 1.])
y_data = np.array([19.46, 17.25, 15.43, 14.14, 13.89, 13.21, 12.84, 12.57, 12.13])

def exponential_func(x, a, b, c, d):
    return a * np.exp(b * x + d) + c

popt, pcov = curve_fit(exponential_func, x_data, y_data, p0=(1, -1, 1, 0))

a_fit, b_fit, c_fit, d_fit = popt
expression = f"{a_fit:.4f} * exp({b_fit:.4f} * x + {d_fit:.4f}) + {c_fit:.4f}"
print("expression：", expression)

x_fit = np.linspace(min(x_data), max(x_data), 100)
y_fit = exponential_func(x_fit, *popt)

plt.plot(x_fit, y_fit, label='Predicted value')
plt.scatter(x_data, y_data, label='Actual')
plt.xlabel('Mixing ratio of DFA/CS')
plt.ylabel('Tar yield')
plt.title('Kinetic model')
plt.legend()
plt.show()

y_pred = exponential_func(x_data, *popt)
comparison_table = np.column_stack((x_data, y_data, y_pred))
print("\nA table comparing predicted values to actual values：")
print("r     Actual      Predicted value")
print("-------------------------")
for row in comparison_table:
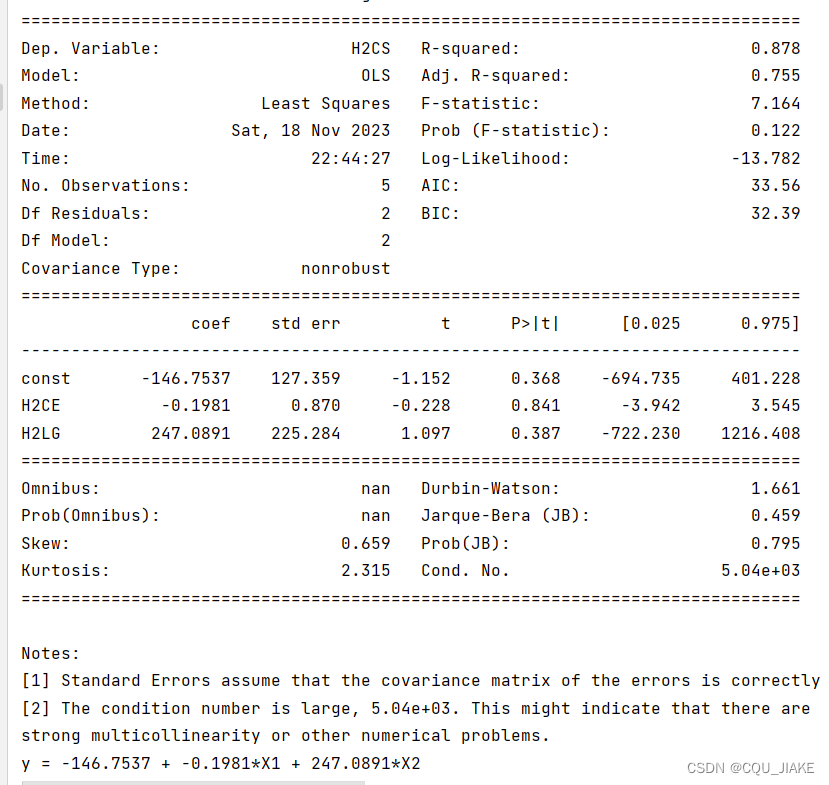
    print(f"{row[0]:.1f}    {row[1]:.2f}    {row[2]:.2f}")

多元线性回归拟合以及摘要

import pandas as pd
import numpy as np
import statsmodels.api as sm
# 指定 Excel 文件路径
excel_file = 'C:/Users/26861/Desktop/Annex II-Pyrolysis Gas Yields of Three Pyrolysis Combinations.xlsx'
# 提取 X 列的数据作为自变量
df = pd.read_excel(excel_file)

X = df[['H2CE', 'H2LG']]
y = df['H2CS']

# 添加常数列
X = sm.add_constant(X)

# 拟合多元线性回归模型
model = sm.OLS(y, X)
results = model.fit()

# 打印回归结果摘要
print(results.summary())
equation = 'y = {:.4f} + {:.4f}*X1 + {:.4f}*X2 '.format(results.params['const'], results.params['H2CE'], results.params['H2LG'])
print(equation)