Linux系统会内置vi文本编辑器
Vim具有程序编辑的能力,可以看做是Vi的增强版本,可以主动的以字体颜色辨别语法的正确性,方便程序设计。代码补完、编译及错误跳转等方便编程的功能特别丰富,在程序员中被广泛使用。
vi和vim常用的三种模式
- 正常模式
以vim打开一个档案就直接进入一般模式了(这是默认的模式)。在这个模式中,你可以使用【上下左右】按键来移动光标,你可以使用【删除字符】或【删除整行】来处理档案内容,也可以使用【复制、粘贴】来处理你的文件数据
- 插入模式
按下i、I、o、O、a、A、r、R等任何一个字母之后才会进入编辑模式,一般来说按i即可
- 命令行模式
先输入esc 再输入: 在这个模式当中,可以提供你相关指令,完成读取、存盘、替换、离开vim、显示行号等的动作则是在此模式当中达成的!
vi和vim基本使用
使用vim开发一个Hello.java程序,保存步骤说明和演示
各种模式的相互切换
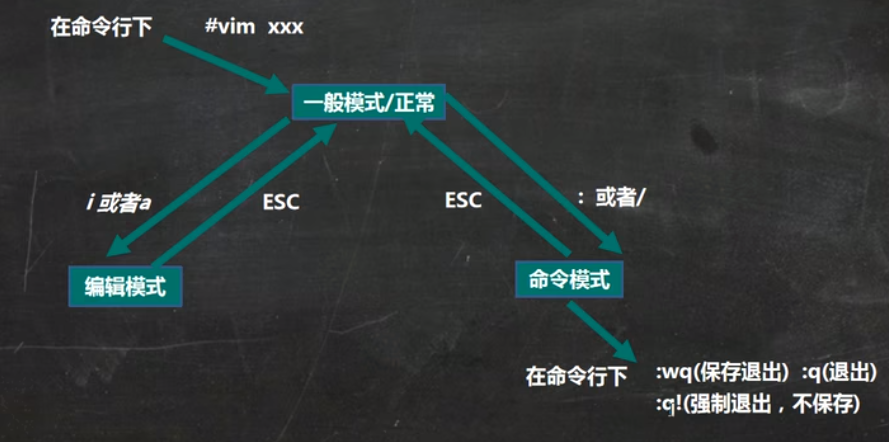
vi和Vim快捷键练习
1.拷贝当前行 yy ,拷贝当前行向下的5行 5yy ,并粘贴(输入p)
2.删除当前行 dd ,删除当前行向下的5行 5dd
3.在文件中查找某个单词 [命令模式下/关键字 ,回车 查找,输入 n就是找下一个]
4.设置文件的行号 ,取消文件的行号 【在命令行 :set nu 和 :set nonu】
5.编辑/etc/profile文件,使用快捷键到该文档的最末行[G]和首行[gg]
6.在一个文件中输入"hello",然后又撤销这个动作 u
7.编辑/etc/profile文件,在一般模式下,并将光标移动到,输入20行,再输入 shift+g




![[黑马程序员SpringBoot2]——开发实用篇2](https://img-blog.csdnimg.cn/c40032139270428b875922c903517c31.png)