1.频率概述

       时域表示给出了信号在采样时刻的幅度。 频率是指循环或周期事件的复现率，对于模拟或数字波形，信号周期的倒数就是频率。快速傅立叶变换 (FFT) 提供了一种检查频域关系的方法。傅里叶定理指出，时域中的任何波形都可以用正弦和余弦的加权和来表示。然后，相同的波形可以在频域中表示为每个分量频率处的一对幅度和相位值。

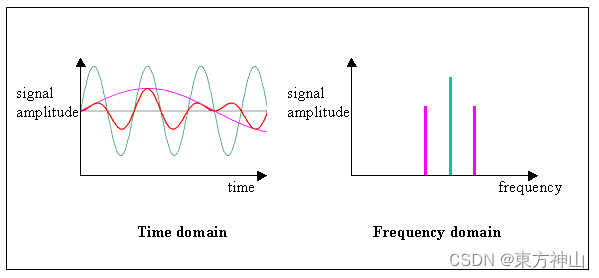
        实际应用中的周期性模拟信号很复杂，很难用简单的正弦曲线来表示。傅里叶分析可将任何复杂波形分解为简单的正弦、余弦或复指数函数之和。信号所包含的频率分量往往是我们所感兴趣的，这种分析称为频域或频谱分析。

        另一方面，数字信号频率的获取相对容易。对于简单的数字信号，如图2所示的信号，周期就是两个上升沿或者下降沿之间的时间间隔。

        如果上升沿或下降沿之间的时间间隔略有不同，则可以通过大量采样后取平均值来确定频率。

2.如何进行频率测量

2.1数字信号

        数字频率采集的过程相当简单。如果是低频信号，只需要使用一个计数器或时基就足够了。输入信号的上升沿触发要计数的时基时钟滴答数。由于时基频率已知，就能简单地计算出输入信号的频率。

         当数字信号的频率很高或不断变化时，最好使用下面介绍的双计数器方法。需要注意的是，两种方法种具有相同的硬件局限性，即所要测量的频率不能超过计数器支持的最大输入频率，但可以超过内部时基频率。 

高频双计数器测量方法
        高频信号测量需要使用两个计数器。    一对（两个）计数器会产生用户指定周期的脉冲序列，“测量时间”远大于待测信号，但又要尽量小，以避免计数器翻转。

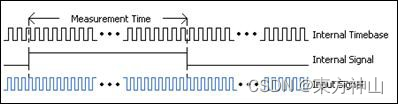
        内部信号的测量时间为内部时基的整数倍，换句话说，两者之间可以整除。 然后，在已知的时间间隔内测量输入信号的时钟滴答数，该时间间隔由内部信号提供。 将时钟滴答数除以已知的测量时间就能够得到输入信号的频率。

 大范围双计数器测量方法

        对于频率会变化的信号，这种双计数器方法可在整个信号范围内提供更高的精度。在这种情况下，输入信号为被除数，已知值为除数。内部时基的时钟滴答数在分频信号处于逻辑高电平时记录下来。 这时就可以算出逻辑高电平的时间，也就是时钟滴答数乘以内置时基的周期时间。这个值再乘以2，就可以获得分频信号的周期（高电平和低电平时间），它是输入信号周期的整数倍。然后对输入信号周期求倒数即可得到频率值。

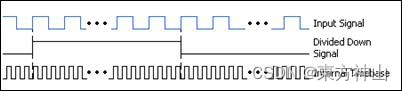
        这一方法相当于在大范围测量后求平均值来得到信号的变化频率，但这种方法还能测量比时基频率更高的输入信号。 

注意：

1. 搜索计数器部分（有时称为“通用计数器”），您将在其中找到以下信息：
   1. 内部基本时钟：计数器的内部基本时钟是导致计数器的值根据门端子的状态递增/递减的信号。
   2. 外部基准时钟频率：如果需要特定的基准时钟频率，大多数 NI 设备都允许使用外部基准时钟。该时钟的用途与内部基本时钟相同，但由用户从外部提供。由于带宽限制，外部基本时钟的最大速率取决于设备的总线。
   3. 基本时钟精度：内部基本时钟的精度直接影响通用计数器的任何测量或频率生成的精度。该精度也继承自整个设备时基精度，这意味着如果外部提供更高精度的主时基，则可以提高该时钟的精度。
2. 您可以使用奈奎斯特定理知道最大频率，该定理告诉我们，如果连续带宽受限信号不包含高于采样频率一半的频率分量，则原始信号可以可以无失真地恢复。因此，您的最大频率将是您正在使用的基本时钟频率的一半。例如，如果您的基本时钟运行在 100 MHz，则最大频率将为 50 MHz。

2.2模拟信号

        某些设备可通过频率－电压电路直接测量模拟频率。然而，某些设备只能测量电压，必须通过软件算法将测量值转换为频率。

        某些用于测量模拟频率的设备（例如，DSA设备和SCXI-1126），通过电路可产生与测量信号具有相同频率的触发。每当信号从“阈值电平-滞后”传递到阈值电平时，将产生触发。脉冲发生器将通过这些触发在每个频率周期生成一个脉冲。输入频率范围用于设置脉冲的宽度。输入频率范围增加时，脉冲宽度将减小。脉冲序列将被转换为直流信号，其电平与脉冲序列的占空比成正比。脉冲发生时，占空比是脉冲序列周期的分数。直流信号的电压与输入频率成正比，因此可换算为该频率值。

        对于无法直接测量频率的设备，需要使用快速傅立叶变换(FFT)等软件算法，将电压转换为频率，采样速率必须大于采样信号最高频率2倍。

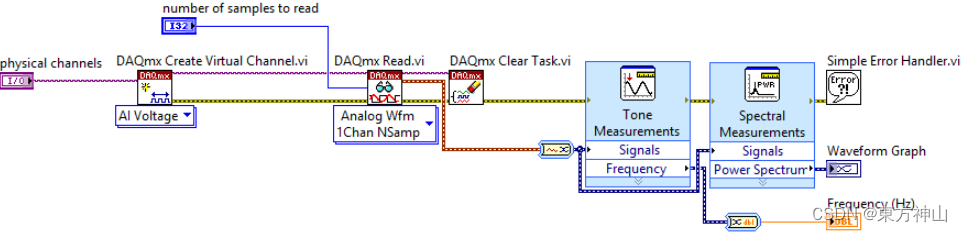
计算方波频率的方法​​​​​​​

​​​​​​​        在软件中实现边沿计数以确定信号的频率。

        请注意，此示例将计算带有噪声数据的额外转换。如果存在噪声，可能需要进行过滤或其他修改以确保准确计数

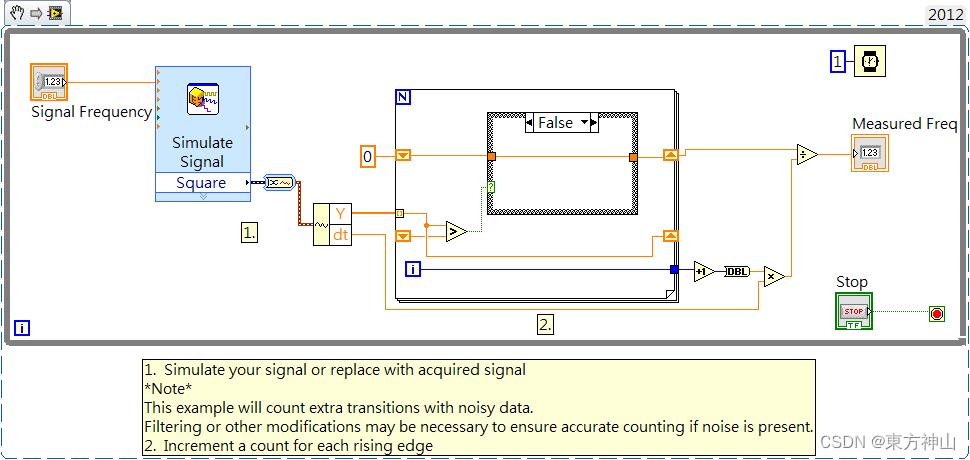
3.在LabVIEW中使用快速傅里叶变换和功率谱 

什么是傅里叶变换？

        傅立叶变换是一种将信号从时域转换到频域（或反之亦然）的数学运算。在现实世界中，时域是常用的。在时域中，信号以时间为基础显示。在频域中，信号是基于频率显示的。

DFT 和 FFT 有什么区别？

        应用于数字（离散）信号而不是模拟（连续）信号的傅里叶变换称为 DFT（离散傅里叶变换）。FFT（快速傅里叶变换）是一种更快的 DFT，如果信号中的样本数量是 2 的幂，则可以应用它。FFT 所需的运算次数约为 N * log 2 (N)，DFT 所需的运算次数约为 N ^ 2，并且 FFT 明显更快。

“交叉功率”VI、“交叉功率谱”VI、“自动功率谱”VI、“功率谱”VI 有什么区别？

        “交叉功率谱”VI 和“自动功率谱”VI 是放置在测量子选板上的高级 VI。其他VI都是低级的。我们通常建议使用高级 VI。“（自动）功率谱”计算信号功率，但相位信息丢失。“交叉功率（频谱）”计算两个信号的功率，并返回频谱之间的相位差。

什么是零填充？

        就是在时域序列的开头和/或末尾添加零。即使添加，也不会对信号的频谱产生影响。当时域序列的长度不是2的幂时，补零是合适的。通过添加零以使序列为 2 的幂，可以更快地完成 FFT 计算。补零还可以提高 FFT 的频率分辨率（参见上面的问题）。

使用FFT VI时，“负频率”存储在哪里？

        FFT VI 位于两侧。这意味着作为傅里叶变换的数学属性出现的负频率包含在VI的输出中。FFT 输出阵列的前半部分包含从 DC (0 Hz) 到奈奎斯特频率的升序频率。阵列的另一半是前半部分的镜像（围绕阵列的中间元件）并且包含负频率。

我应该将什么连接到 dt 输入？

        dt 是时域输入信号中样本之间的时间。如果获取信号的采样率 (fs) 已知，则可以根据 dt = 1 / fs 进行计算。

理论知识可参考此链接：Using Fast Fourier Transforms and Power Spectra in LabVIEW - NI

 4.频率测量的三种方法

Making Accurate Frequency Measurements - NI