无向基环树

找环，题目

拓扑排序找环

#include <bits/stdc++.h>
using namespace std;

// 点的编号从1开始
const int N = 100010;
int n;
vector<int> g[N];
vector<int> in, visit;

void topologicalOrder() {
	queue<int> q;
	//把入度为1的点入队
	for (int i = 1; i <= n; i++) {
		if (in[i] == 1) q.push(i), visit[i] = 1;
	}
	while (q.size()) {
		int u = q.front();
		q.pop();
		for (int v: g[u]) {
			in[v]--;
			if (in[v] == 1) q.push(v), visit[v] = 1;
		}
	}
}

void print() {
	for (int i = 1; i <= n; i++) 
		if (!visit[i]) cout << i << " ";
}

int main()
{
	cin >> n;
	in = vector<int>(n);
	visit = vector<int>(n);
	for (int i = 1; i <= n; i++) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
		in[u]++;
		in[v]++;
	}
	topologicalOrder();
	print();
	return 0;
}

并查集找环

#include <bits/stdc++.h>
using namespace std;

// 并查集模板
struct DSU {
    std::vector<int> f, siz;
    
    DSU() {}
    DSU(int n) {
        init(n);
    }
    
    void init(int n) {
        f.resize(n);
        std::iota(f.begin(), f.end(), 0);
        siz.assign(n, 1);
    }
    
    int find(int x) {
        while (x != f[x]) {
            x = f[x] = f[f[x]];
        }
        return x;
    }
    
    bool same(int x, int y) {
        return find(x) == find(y);
    }
    
    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }
    
    int size(int x) {
        return siz[find(x)];
    }
};

// 点的编号从1开始
const int N = 100010;
int n;
vector<int> g[N];
vector<int> path;

void findRing(int pre, int u, int v, int index) {
	path[index] = u;
	if (u == v) {
		sort(path.begin(), path.begin() + index + 1);
		for (int i = 0; i <= index; i++) cout << path[i] << " ";
		return ;
	}
	
	for (int j: g[u]) {
		if (j == pre) continue;
		findRing(u, j, v, index + 1);
	}
}

int main()
{
	cin >> n;
	DSU dsu(n);
	path = vector<int>(n);
	for (int i = 1; i <= n; i++) {
		int u, v;
		cin >> u >> v;
		if (dsu.find(u) != dsu.find(v)) {
			// 两个点不联通
			g[u].push_back(v);
			g[v].push_back(u);
			dsu.merge(u, v);
		} else {
			// u和v已经联通了，那么我们在图中寻找从u到v的路径，这些都是环上的点
			findRing(-1, u, v, 0);
		}
	}
	return 0;
}

dfs找环

#include <bits/stdc++.h>
using namespace std;


// 点的编号从1开始
const int N = 100010;
int n, idx;
vector<int> g[N];
vector<int> path, dfn, fa;

void dfs(int u){
	if (dfn[u] != 0) return ;
    dfn[u]=++idx;
    for(int v: g[u]){
        if(v==fa[u]) continue;
        if(!dfn[v]) fa[v]=u,dfs(v);
        else {
			if(dfn[v]<dfn[u]) continue;
			path.push_back(v);
			for(; v != u; v=fa[v]) path.push_back(fa[v]);
		}
    } 
    return;
}


int main()
{
	cin >> n;
	idx = 0;
	dfn = vector<int>(n + 1);
	fa = vector<int>(n + 1);
	for (int i = 1; i <= n; i++) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	for (int i = 1; i <= n; i++) dfs(i);
	sort(path.begin(), path.end());
	for (int v: path) cout << v << " ";
	return 0;
}

内向基环树

每个点有且只有一个出边

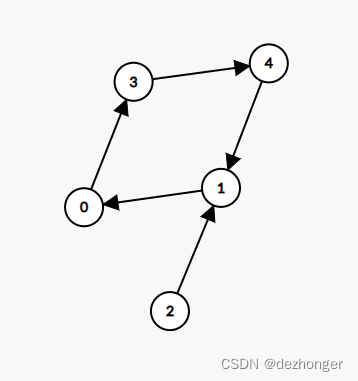
2876. 有向图访问计数

class Solution {
public:
    vector<int> countVisitedNodes(vector<int>& g) {
        int n = g.size(); //节点的个数，节点的编号从0开始
        vector<vector<int>> rg(n); //反图
        vector<int> in(n);
        for (int x = 0; x < n; x++) {
            int y = g[x];
            // 一条从x到y的边: x -> y
            in[y]++;
            rg[y].push_back(x); //添加反向边到反图中
        }
        
        // 拓扑排序，剪掉g上所有的树枝
        queue<int> q;
        for (int i = 0; i < n; i++) if (in[i] == 0) q.push(i);
        while (q.size()) {
            int x = q.front();
            q.pop();
            int y = g[x];
            if (--in[y] == 0) q.push(y);
        }
        
        //答案数组, 表示的是从i点出发能访问到的节点数
        vector<int> ans(n, 0);
        
        function<void(int, int)> rdfs = [&](int x, int depth) {
            ans[x] = depth;
            // 以环上的点为根，通过反向边去搜树枝点
            // in[y]==0: 树枝点
            for (int y: rg[x]) if (in[y] == 0) rdfs(y, depth + 1);
        };
        
        for (int i = 0; i < n; i++) {
            // 0: 树枝点 -1: 基环上的点
            if (in[i] <= 0) continue;
            
            vector<int> ring;
            for (int x = i; ; x = g[x]) {
                in[x] = -1; // 基环上的点标记为-1，避免重复访问
                ring.push_back(x);
                if (g[x] == i) break; // 回到起点i了
            }
            for (int x: ring) rdfs(x, ring.size());
        }
        return ans;
    }
};

2127. 参加会议的最多员工数

class Solution {
public:
    int maximumInvitations(vector<int>& favorite) {
        int n = favorite.size();
        vector<int> in(n);
        // x -> y
        for (int y: favorite) in[y]++;
        vector<vector<int>> rg(n); // 反图
        
        queue<int> q;
        for (int i = 0; i < n; i++) if (in[i] == 0) q.push(i);
        while (q.size()) {
            int x = q.front();
            q.pop();
            int y = favorite[x];
            rg[y].push_back(x);
            if (--in[y] == 0) q.push(y);
        }
        
        // 在反图上搜索树枝上最深的链
        function<int(int)> rdfs = [&](int x) -> int {
            int max_depth = 1;
            for (int son: rg[x]) max_depth = max(max_depth, rdfs(son) + 1);
            return max_depth;
        };
        
        int max_ring_size = 0, sum_chain_size = 0;
        for (int i = 0; i < n; i++) {
            if (in[i] == 0) continue;
            
            // 搜索基环上的点
            in[i] = 0; //标记，避免重复访问
            int ring_size = 1;
            for (int x = favorite[i]; x != i; x = favorite[x]) {
                in[x] = 0;
                ring_size++;
            }
            
            if (ring_size == 2) sum_chain_size += rdfs(i) + rdfs(favorite[i]);
            else max_ring_size = max(max_ring_size, ring_size);
        }
        return max(max_ring_size, sum_chain_size);
    }
};