算法之冒泡排序
冒泡排序Bubble Sort
- 交换排序
- 相邻元素两两比较大小,有必要则交换。
- 元素越小或越大,就会在数列中慢慢的交换并“浮”向顶端,如同水泡咕嘟咕嘟往上冒。
核心算法
- 排序算法,一般都实现为就地排序,输出为升序
- 扩大有序区,减小无序区。图中红色部分就是增大的有序区,反之就是减小的无序区
- 每一趟比较中,将无序区中所有元素依次两两比较,升序排序将大数调整到两数中的右侧
- 每一趟比较完成,都会把这一趟的最大数推倒当前无序区的最右侧
nums = [1, 9, 8, 5] # 定义一个nums变量
#length = len(nums)
j = 0
for j in range(3): # 定义一个for循环,
if nums[j] > nums[j+1]: # if判断,索引0 大于 索引1
nums[j], nums[j+1] = nums[j+1], nums[j] # 就进行两两交换,直到把最大一个数交换到列表尾端,变成有序区
print(nums) # 第一次交换完打印
j = 1
for j in range(2):
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
print(nums)
# 返回结果:[1, 8, 5, 9]
# 返回结果:[1, 5, 8, 9]
# 优化
nums = [1, 9, 8, 5]
length = len(nums)
for i in range(length - 1):
for j in range(length - 1 - i): # length - 1 - i 3 - 0 j = 0 1 2
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
print(nums)
# 先取出nums的长度,length,通过迭代length的值可以确定循环执行的范围。
# 返回结果:[1, 5, 8, 9]
nums = [1, 9, 8, 5, 4, 3, 2, 7, 6]
length = len(nums)
for i in range(length - 1):
for j in range(length - 1 - i): # length - 1 - i 3 - 0 j = 0 1 2
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
print(nums) # 这个打印,是打印循环每次执行的结果
print(nums)
# 返回结果:[1, 5, 8, 9]
图一
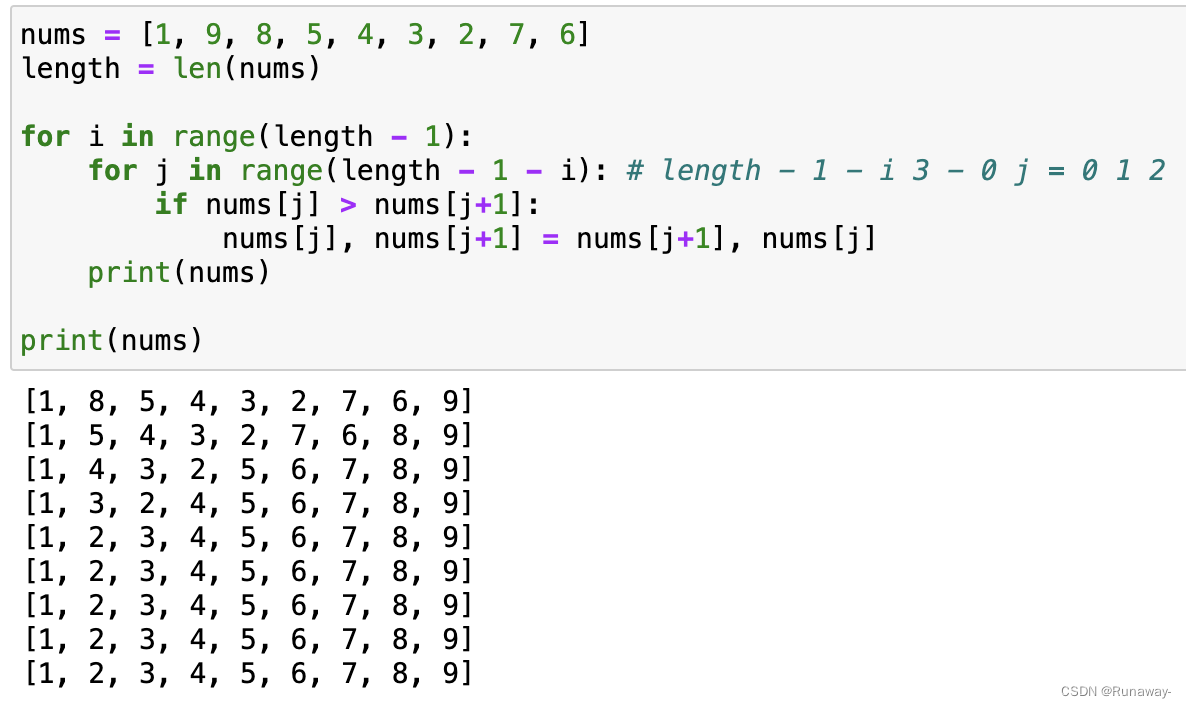
可以看到后4趟执行的结果是没有变化的,就是执行了无用的循环。
# 优化
nums = [1, 9, 8, 5, 4, 3, 2, 7, 6]
length = len(nums)
count = 0 # 表示执行的次数
count_swap = 0 # 表示交换的次数
for i in range(length - 1):
swapped = False # 如果发生变化就是True,没有发生变化才是False
for j in range(length - 1 - i): # length - 1 - i 3 - 0 j = 0 1 2
count += 1
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
swapped = True
count_swap += 1
print(nums)
if not swapped: # 条件判断,如果没有发生交换
break # break 终止循环
print(nums)
print(count, count_swap)
图二

上面代码执行结果。
# 最终代码
nums = [1, 9, 8, 5, 4, 3, 2, 7, 6] # 定义一个无序区
length = len(nums) # nums的长度
for i in range(length - 1): #循环与次数相关就是O(n) # i循环控制趟数
swapped = True # 用于终止循环的条件
for j in range(length - 1 - i): #循环与次数相关就是O(n) # j循环控制比较,有序区与无序区
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j]
swapped = False
if swapped: # 如果swapped的值是True就证明没有在进行交换了。
break # 终止循环
print(nums) # O(n * n) O(n**2) On方
# 循环的时间复杂度是O(n), 双层循环的时间复杂度是O(n**2)也就是On方
# 返回结果:[1, 2, 3, 4, 5, 6, 7, 8, 9]