一 - 前言
介绍:大家好啊,我是hitzaki辰。
社区:(完全免费、欢迎加入)日常打卡、学习交流、资源共享的知识星球。
自媒体:我会在b站/抖音更新视频讲解 或 一些纯技术外的分享,账号同名:hitzaki辰。
正文开始,抓紧上车!

二 - 题干讲解
编写一个算法来判断一个数
n是不是快乐数。「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果
n是 快乐数 就返回true;不是,则返回false。力扣原题:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
1 - 快乐数的迭代不会无限变大
1)举例1:8迭代后变为64,变大了
2)举例2:三位数的最大值999,迭代后为243
即快乐数不会无限变大。
2 - 总结
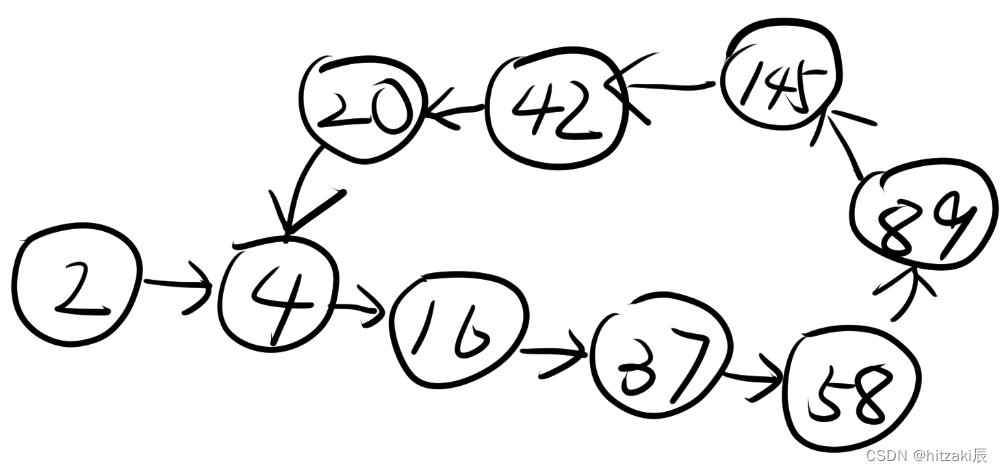
快乐数的迭代进行到最后只有两种情况:
(1)终止:变成1,比如68->100->1
(2)无限循环:迭代到最后,重新成为迭代链路前面的点,即形成环路
3 - 经典解法
使用一个Set存储出现过的数字,若迭代过程中重复出现了一个数字,则意味着出现了环路
三 - 双指针法,将迭代链路视为一个链表
1 - 如何判断一个链路有环
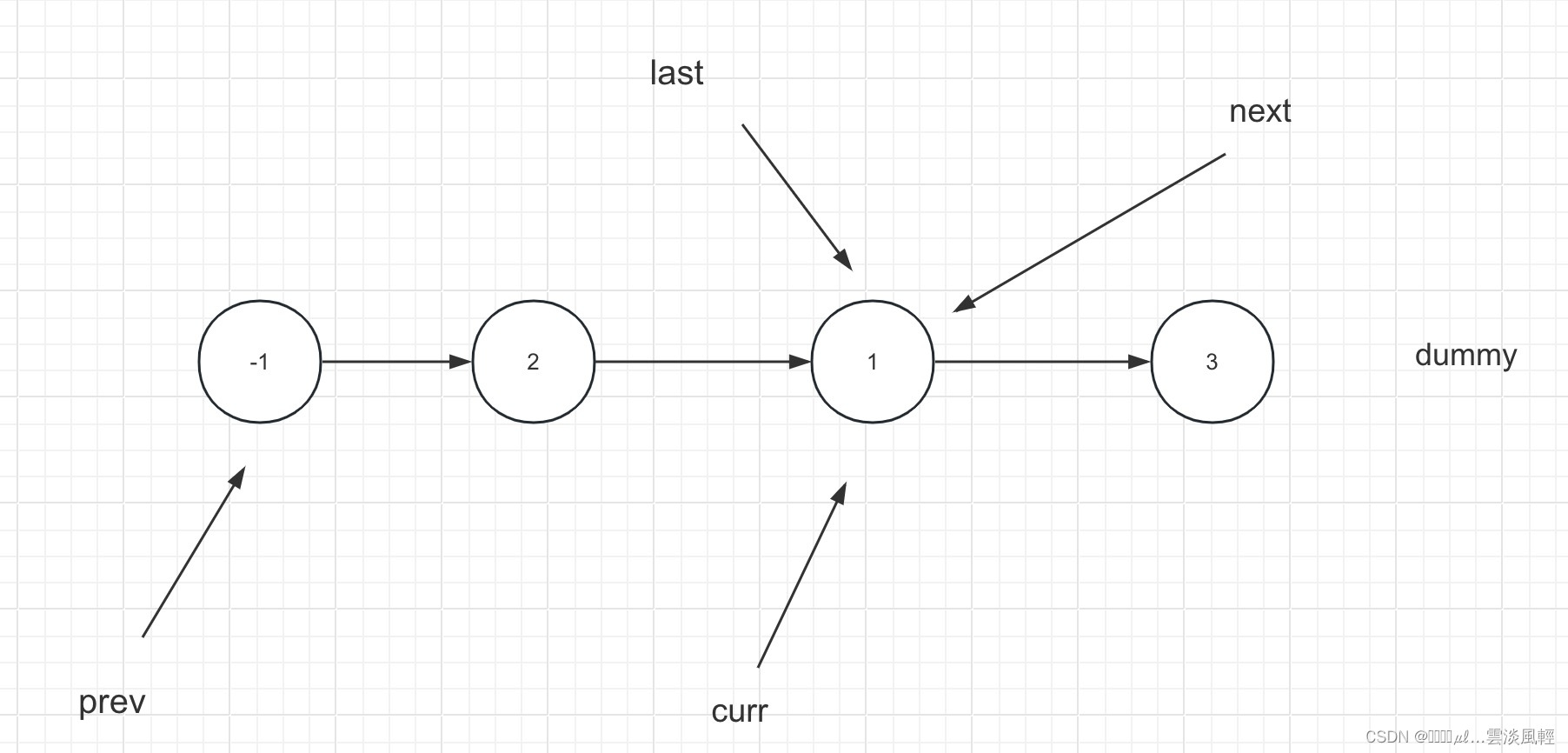
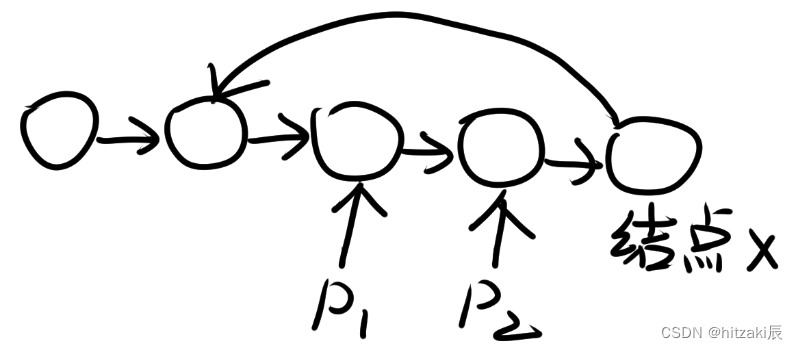
一个环形链表,使用指针p1和p2,p1每次迭代两个,p2每次迭代1个,如果有环,则p1、p2一定相遇。
如图,p1和p2指针下一次迭代一定会在结点x相遇。
2 - 快乐数的代码实现
根据上述的理论基础,我们可以同时对p1和p2进行快乐数迭代,
通过判断结果为1或者p1、p2是否相等,来决定这个数是否为快乐数。
class Solution {
public boolean isHappy(int n) {
int fast = happy(n), slow = n;
while(fast!=1){
if(fast == slow) return false;
fast = happy(fast);
fast = happy(fast);
slow = happy(slow);
}
return true;
}
private int happy(int n){
int result = 0;
while(n!=0){
int bit = n % 10;
result += bit * bit;
n = n / 10;
}
return result;
}
}四 - 结尾
感谢你看到这里,如果感觉内容不错的话请点赞支持一下!
如果小伙伴对我的讲解有疑问,欢迎评论区讨论。



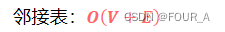



![[ 一刷完结撒花!! ] Day50 力扣单调栈 : 503.下一个更大元素II |42. 接雨水 | 84.柱状图中最大的矩形](https://img-blog.csdnimg.cn/16624f0dbb754a7587572cd9629dba35.png)