时间序列与 statsmodels:预测所需的基本概念(2)

![]()
维托米尔·约万诺维奇
跟随
走向发展
8
一、说明
在使时间序列平稳后,在本博客中我们应用 SARIMAX 预测并进行深入解释。
二、关于平稳性
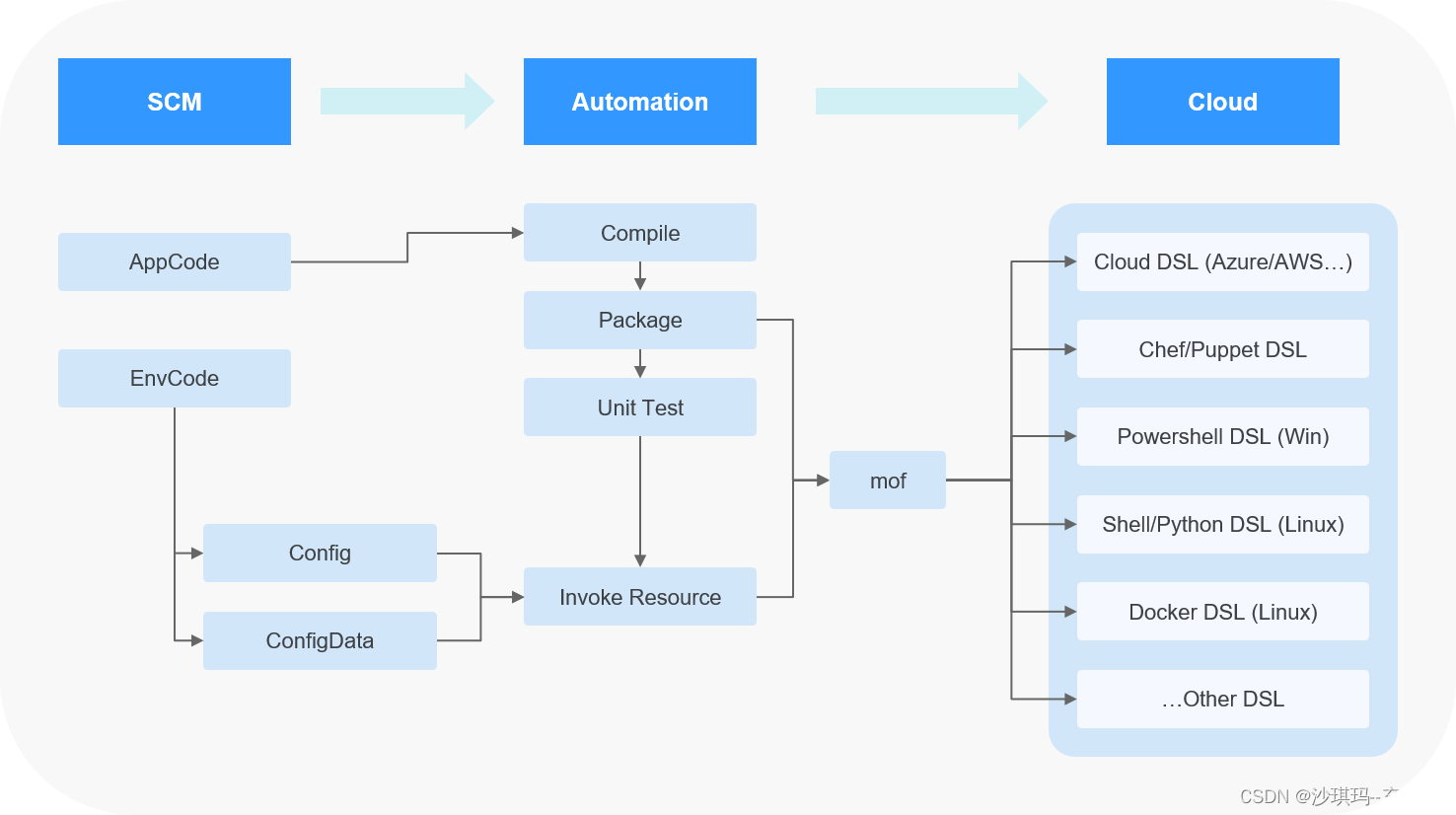
平稳性是一个重要的概念,它告诉我们我们已经“阅读”了时间序列中模式的所有组成部分。现在我们将使用简单的 statsmodels 包制作非常简单的 SARIMAX 模型,了解数据的所有参数。这基本上与 ARIMA 非常相似,但只有季节性成分。ARIMA 中的 AR 指的是自回归参数,它基本上告诉我们时间序列的“记忆”有多复杂。Yt 是我们的预测,而 b0 是截距,b1 是权重,与线性回归中相同,而 wt 是白噪声(时间序列的随机性)。
AR (1): Yt = b0 + b1 * Yt-1 + wt
AR (2): Yt = b0 + b1 * Yt-1 + b2 * Yt-2+ wt
如果需要,也可以增加此 AR 参数。另一方面,ARIMA 中的 I 分量指的是差分参数,它告诉我们从一个时间点到另一个时间点减去时间序列的次数(即 pandas 平移方法)。具有强记忆成分的时间序列必须进行差分,有的甚至是两次(二阶差分)。差分应该使我们摆脱时间序列的随机游走,这是随机性,但取决于时间(即它有某种记忆=你可以在这里看到更多信息)。最后一个参数MA是移动平均线,与平滑有关,但这里我们没有篇幅特别关注他。SARIMAX 中的 S 表示季节性成分,而名称中的 X 还提供了包含外生预测变量的可能性,但在本例中该预测变量并不存在。
2.1 萨利麦克斯SARIMAX
让我们看看如何使用 statsmodels 中 SARIMAX 实现的类来进行预测。但首先,我们将进行小火车测试分割功能,然后做出预测。然后我们将创建一个函数来预测所需的滞后数。我们想要对明年进行预测,因此我们将用 12 个月进行预测。
def train_test_split(timeseries, lags_for_prediction=12):
split=len(timeseries)-lags_for_prediction
train=timeseries[:split]
test=timeseries[split:]
return train, test
train_series, test_series = train_test_split(data, 12)我们的差分参数必须是2,AR参数也是如此。我们这里没有空间来解释 MA 参数,所以我们只取 1。
#season - S (seasonal parameter)
#p - AR (autocorrelation parameter)
#d - I(differencing parameter)
#q - MA (moving average parameter)
#cov - X (exogenous predictor) - not used
import statsmodels.api as sm
def forecasting (p,d,q, season, lags_for_forecast):
model = sm.tsa.statespace.SARIMAX(train_series, order=(p,d,q), seasonal_order=(p,d,q,season),
simple_differencing=0,
enforce_stationarity=True,
enforce_invertibility=False)
fitted = model.fit(disp=-1)
# Forecast
forecast = fitted.forecast(lags_for_forecast)
# Plot
plt.figure(figsize=(12,5), dpi=100)
plt.plot(train_series, color='blue', label='train')
plt.plot(test_series, color='green', label='test', alpha=0.6)
plt.plot(forecast, color='red', label='forecast')
plt.title('Forecast vs Actuals')
plt.legend(loc='upper left', fontsize=8)
plt.show()
RSS=np.sqrt(sum(forecast.values-test_series.values.reshape(-1))**2)/lags_for_forecast
print("\n", '\033[1m' +'Root Squared Error (RSS) of SARIMAX model(p,d,q)(p,d,q,s)' + '\033[0m',(p,d,q),(p,d,q, season),':', round(RSS, 3),"\n")
print(fitted.summary())
return fitted, forecast, model
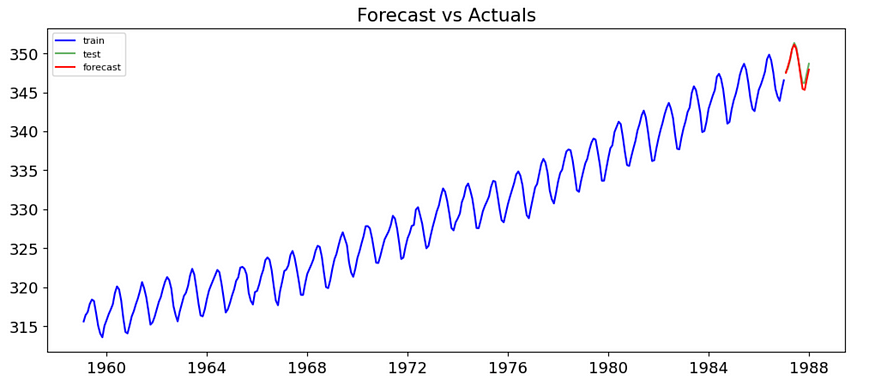
fitted, forecast, model = forecasting (2,2,1, 12, 12)我们使用季节参数为 12 的此函数,因为我们有每月数据,并且我们的时间序列对年份水平有季节性影响(夏季旅行较多),并且我们还使用 12 作为 lags_for_forecast,因为我们想要预测明年(在这个例子中,我们将其与真实的测试数据进行比较,但在这一步之后,我们可以对未来进行真正的预测,而这无法通过某些准确性指标来真正评估)。
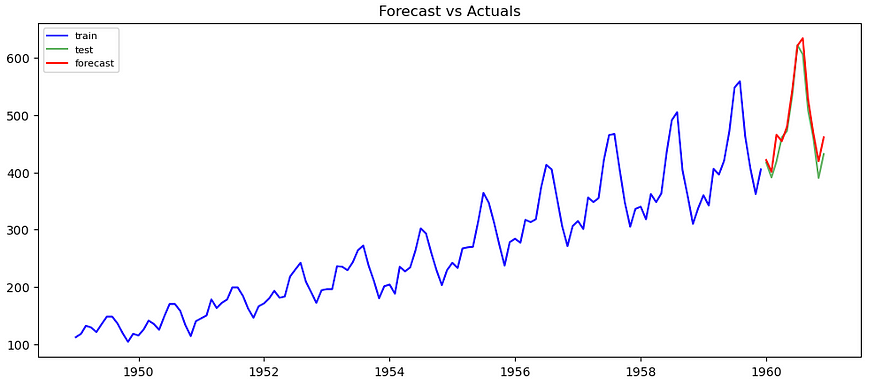
预测值与测试数据
在这里我们可以看到,我们显然进行了良好的超参数调整,并成功地做出了相当令人满意的预测。摘要报告可以让我们更深入地了解模型参数的统计显着性,而 15 名乘客的误差直观上看起来相当不错:
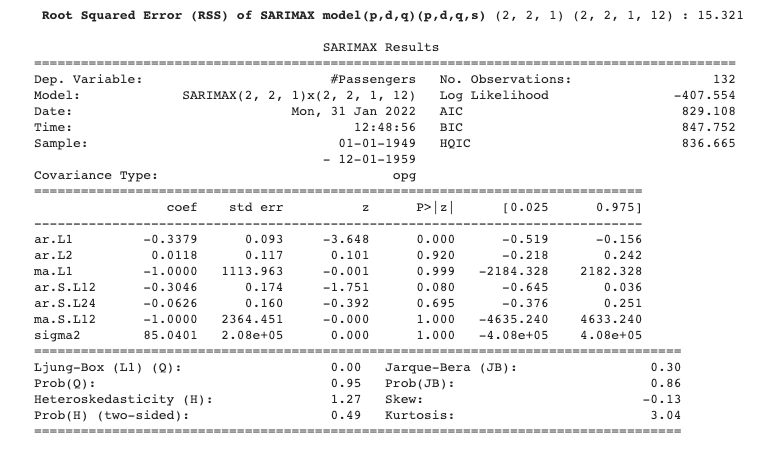
SARIMAX 模型总结
此输出可能表明我们也可以尝试使用 AR=1 作为可能的超参数。
您还可以尝试 statsmodels 的一些很酷的特性和功能,例如检查残差的正态性并查看密度函数,以及一个模块中的相关图(拟合值上的plot_diagnostics ):
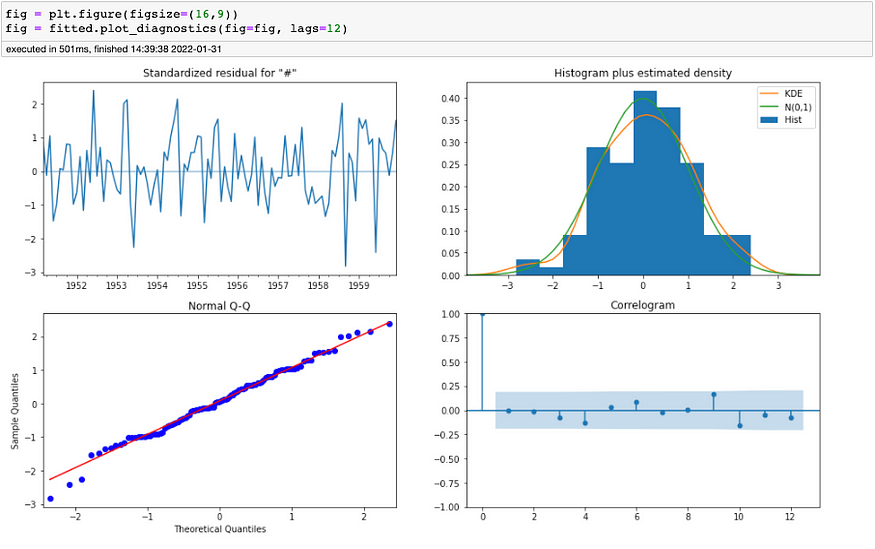
时间序列快速探索模块
恭喜!这是单变量时间序列建模的基本方法。对于单变量时间序列来说,这可能是非常有效的模型。但也要记住,您还可以使用更先进的技术,包括使用外生预测变量进行建模、使用长短期神经网络 (LSTM),还可以使用集成方法,例如光梯度增强或其他依赖于决策树的技术。
在下一篇博客中,我可以写关于超参数调整、Akaike 信息标准 (AIC) 的内容,它可以帮助我们找到高效且简约的模型。该标准可用于自动超参数调整,但让我们一步一步进行。这对于开始来说就足够了。完整的代码可以在这里找到。