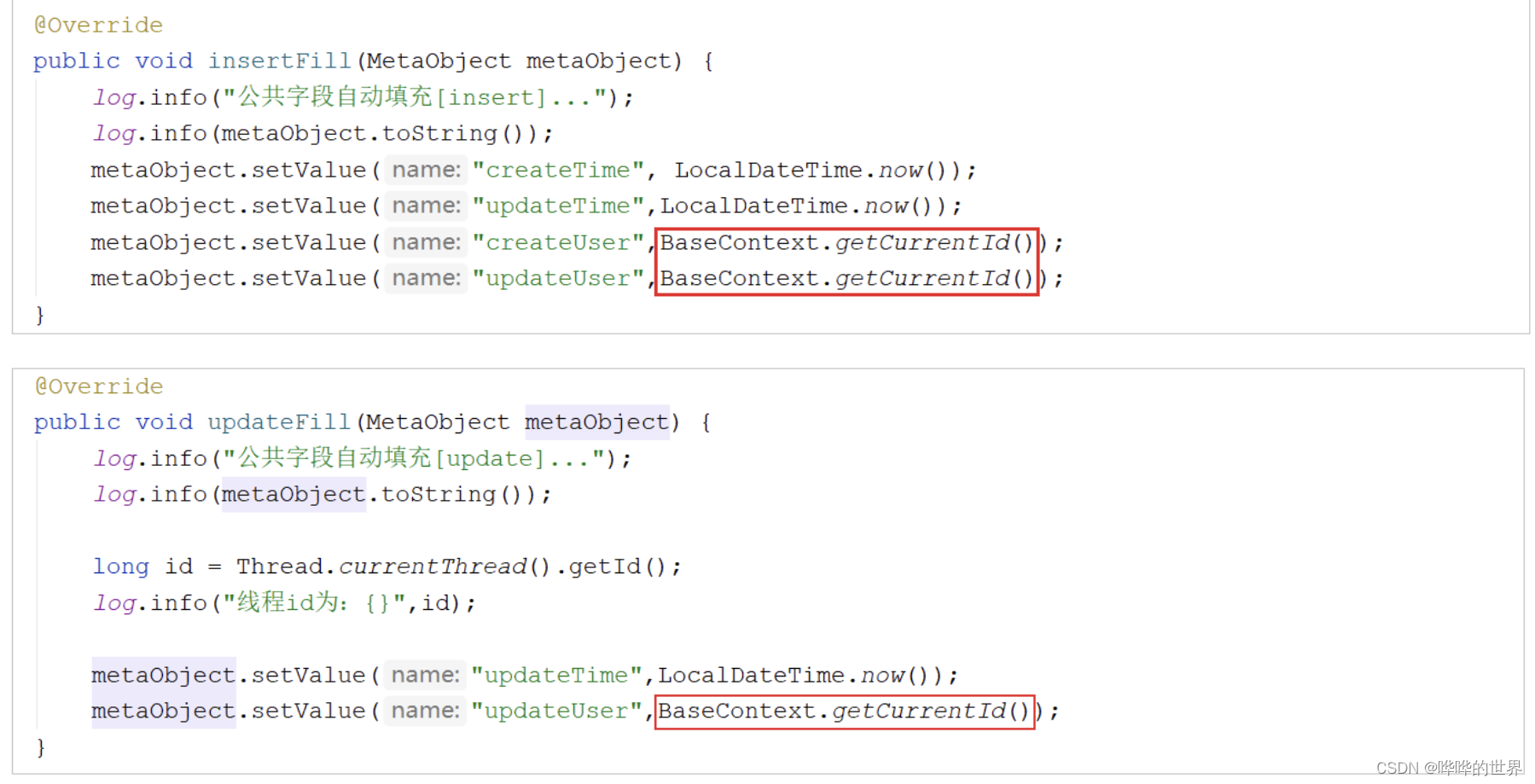
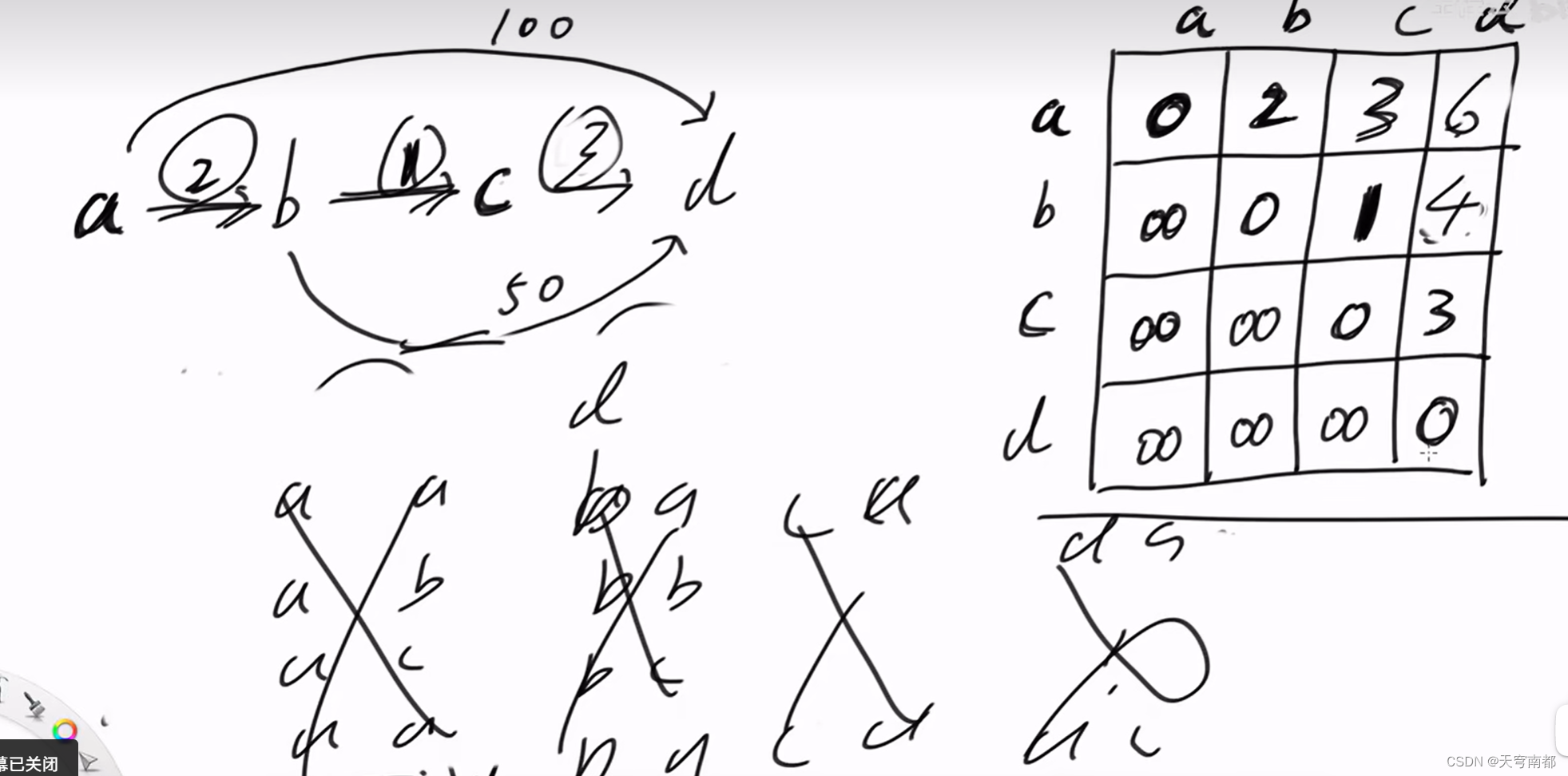
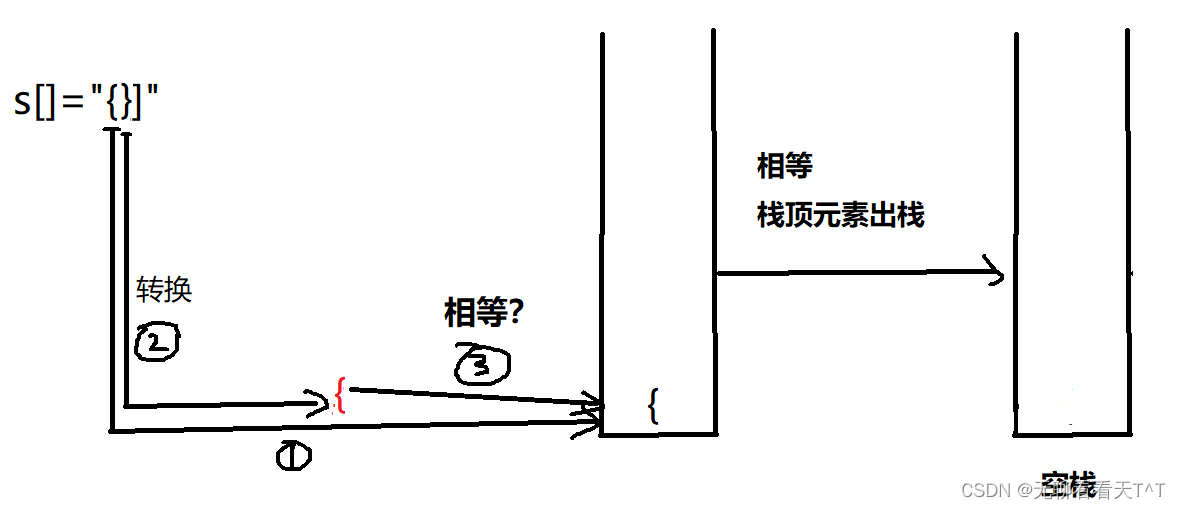
A. Game with Integers
签到题,但是本蒟蒻11分钟才AC,主要还是英文题面不熟练,题目中加粗了after,只有下一步操作之后能被整除才胜利。
英文题面的加粗单词很重要,注意提高签到题速度。
B. 250 Thousand Tons of TNT
被英文题面卡了两发。

The first k boxes,The second k boxes...意思是每连续k个分别入卡车,不是你自由能选的。
C. Yarik and Array
同样被英文题面误导了,但是做到过类似的题目,正解可以是栈或者dp。
每个数值入栈一次,如果栈顶和当前值奇偶性不同则入栈(注意负数用%2判断要取绝对值),不能入栈就先清空栈,再入栈。
用一个值sum动态维护栈的总和,如果sum<0,那么这一串区间对最终答案就是负贡献,清空栈。

subarray,指的是原序列中一串连续的子序列,当然也可以是array本身。
斜体单词也重要。
补题:D. Yarik and Musical Notes
看懂简单,但是做本蒟蒻就做不出来了 :)
化简题面就一个式子。
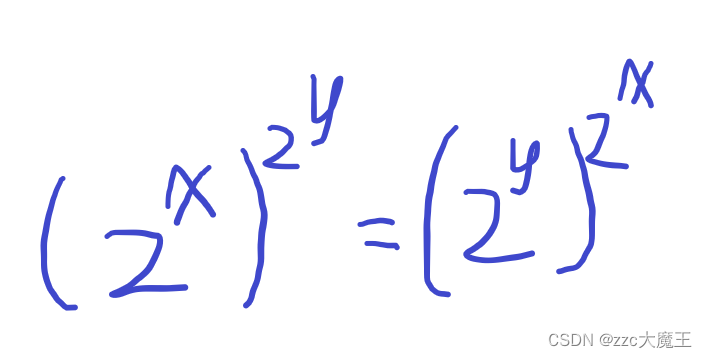
你需要判断对于任意的x和y,是否能使等式相等。(x和y就是题目中a序列的取值)
式子化简步骤:
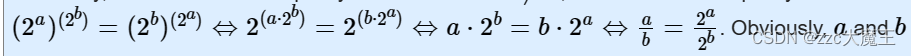
第一步化简,幂的乘方法则:幂的乘方,底数不变,指数相乘。
第二步化简,取二的对数。
第三步化简,换了一下位置。
后续没有化简了,我们自行修改。

根据右式可以发现,等式若成立左右取值均为2的幂次。
显然有式子
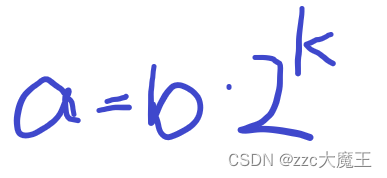
成立,这样左式相除之后才能是2的幂次。(其中k>=0)
代入a
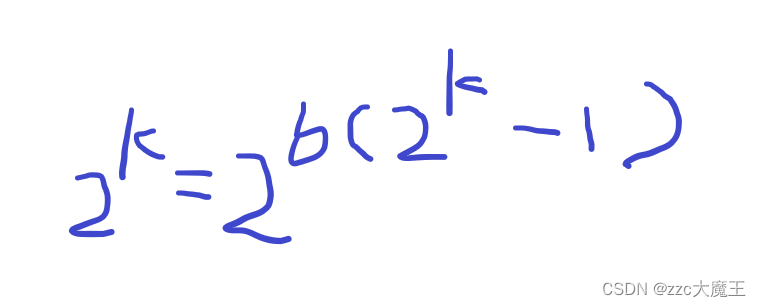
再次处理
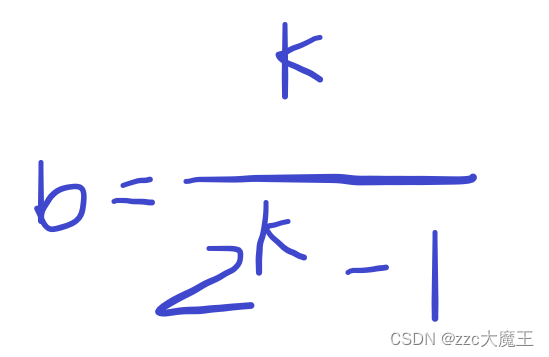
a=b*2^k
k=0,即a=b
k=1,即b=1,a=2
k>=2,b再也取不到整数了。
也就是说这道题只要两个for,枚举一下原序列去配对一下就好了。
但是数据范围是2e5级别的,n^2过不了,考虑优化枚举过程。
优化
2能被配对的次数是前面1出现的次数和2出现的次数。
3能被配对的次数的前面3出现的次数。
那么用哈希表记录一下每个数出现的次数即可。
注意
n的范围是2e5,假设所有数都能被配对,答案极限会爆int范围,记得开long long。
上面b=2,a=1,a和b是任取的,所以前面的1可以对后面的2,前面的2也可以对后面的1。
多次测试记得初始化。
AC代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0;char c=getchar();
while(c<48 or c>57)c=getchar();
while(c>=48 and c<=57)x=(x<<3)+(x<<1)+(c xor 48),c=getchar();
return x;
}
int n,ans;
map<int,int>f;
void solve(){
f.clear();
ans=0;
n=read();
for(int i=1,t;i<=n;++i){
t=read();
ans+=f[t];//相同配对
if(t==2)ans+=f[1];
if(t==1)ans+=f[2];
f[t]++;
}
cout<<ans<<endl;
}
signed main(){
int t=read();
while(t--)solve();
return 0;
}