单源最短路

Dijkstra算法

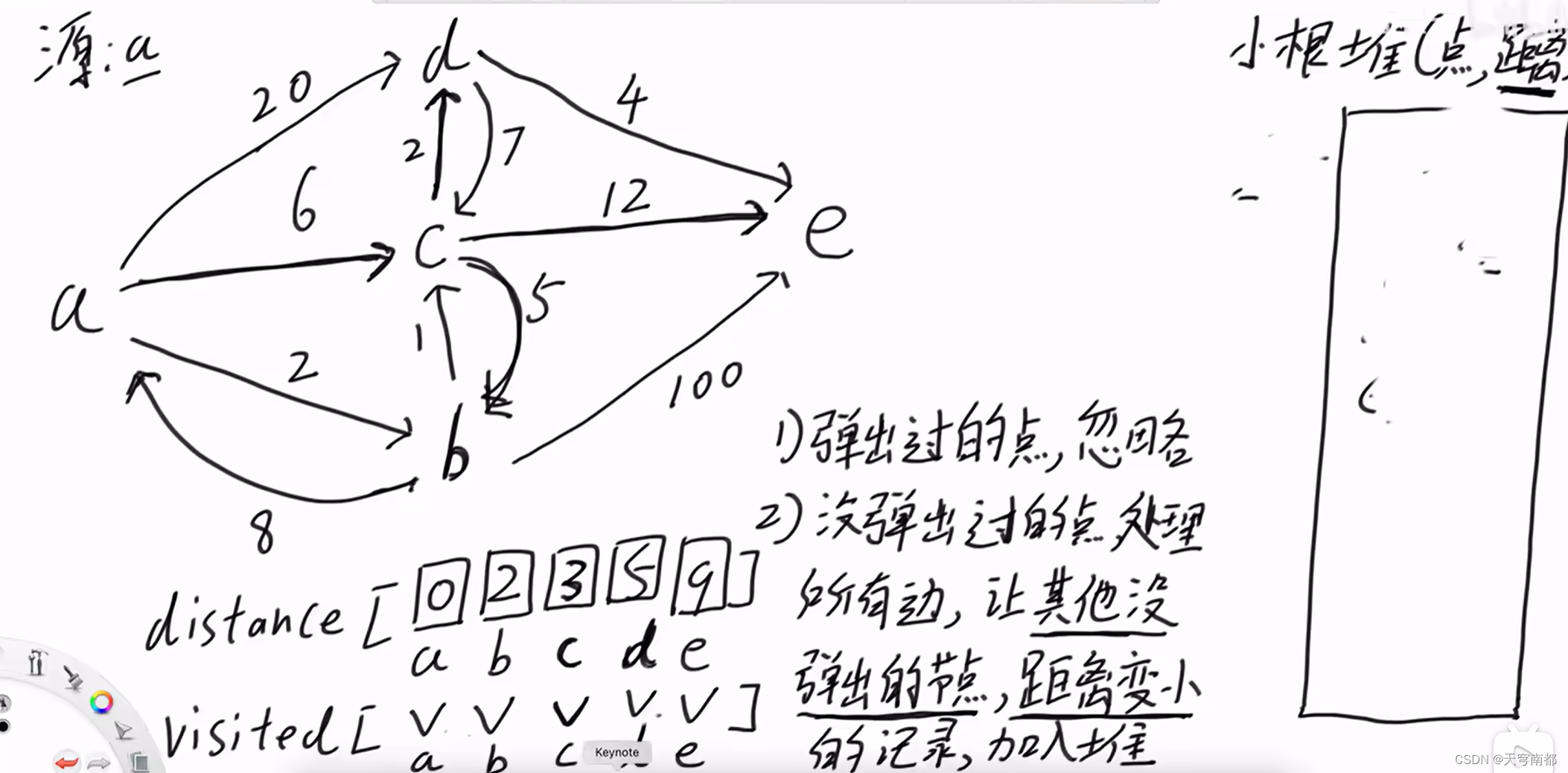
力扣 743.网络延迟时间

const int N = 7777;
int INF = 0x3f3f3f3f;
class Solution {
    struct edge {
        int v, w;
    };
    vector<edge> e[N];
    int d[N], vis[N];  //d数组存储最短路径长度
    priority_queue <pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        for (vector<int> ed : times) {
            e[ed[0]].push_back({ ed[1],ed[2] });
        }
        for (int i = 1; i <= n; i++) {
            d[i] = INF;
        }
        d[k] = 0;  //源点为0
        //first:源点到节点距离
        //second:节点
        heap.push({ 0,k });  
        while(!heap.empty()) {
            int u = heap.top().second;
            heap.pop();
            if (vis[u])
                continue;
            vis[u] = true;
            for (auto ed : e[u]) {
                int v = ed.v;
                int w = ed.w;
                if (!vis[v] && d[u] + w < d[v]) {
                    d[v] = d[u] + w;
                    heap.push({ d[u] + w, v });
                }
            }
        }
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            if (d[i] == INF)
                return -1; 
            ans = max(ans, d[i]);
        }
        return ans;
    }
};

洛谷模板

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<cmath>
using namespace std;
const int N = 5e5 + 10, INF = 0x3f3f3f3f;
struct edge {
	int v, w;
};
vector<edge> e[N];
int d[N], vis[N];  //d[i]表示源点到i点最短距离 ,vis表示是否从小根堆弹出过
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;

int main() {
	int n, m, s;
	scanf("%d%d%d", &n, &m, &s);
    //邻接表建图
	for (int i = 0; i < m; i++) {
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		e[u].push_back({ v,w });
	}
	for (int i = 1; i <= n; i++) {
		d[i] = INF;
	}
	d[s] = 0;  //源点初始化为0
	heap.push({ 0,s });
	while (!heap.empty()) {
		auto u = heap.top().second;
		heap.pop();
		if (vis[u])
			continue;
		vis[u] = true;
		for (auto& ed : e[u]) {
		//first:源点到节点距离
		//second:节点
			int v = ed.v;
			int w = ed.w;
			if (!vis[v] && d[u] + w < d[v]) {
				d[v] = d[u] + w;
				heap.push({ d[u] + w, v });
			}
		}
	}
	for (int i = 1; i <= n; i++)
		printf("%d ", d[i]);
}

A*算法

const int N = 1001;

class Solution {
	int move[5] = { 1,0,-1,0,1 };
	int d[N][N];
	bool vis[N][N];
	struct edge {
		int x, y, w;
		bool operator>(const edge& other)const {
			return this->w > other.w;
		}
	};
	priority_queue<edge, vector<edge>, greater<edge>>heap;
public:
	//曼哈顿距离
	int f(int x, int y, int targetX, int targetY) {
		return abs(x - targetX) + abs(y - targetY);
	}

	int minDistance2(vector<vector<int>>& grid, int startX, int startY, int targetX, int targetY) {
		if (grid[startX][startY] == 0 || grid[targetX][targetY] == 0)
			return -1;
		int n = grid.size();
		int m = grid[0].size();
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				d[i][j] = INT_MAX;
			}
		}
		d[startX][startY] = 1;
		heap.push({ startX,startY,1+f( startX, startY, targetX, targetY)});
		while (!heap.empty()) {
			auto cur = heap.top();
			int x = cur.x;
			int y = cur.y;
			if (vis[x][y])
				continue;
			vis[x][y] = true;
			for (int i = 0; i < 4; i++) {
				int nx = move[i] + x;
				int ny = move[i + 1] + y;
				if (nx >= 0 && ny >= 0 && nx < n && ny < m && !vis[nx][ny]) {
					d[nx][ny] = d[x][y] + 1;
					heap.push({ nx,ny,1 + d[x][y] + f(nx,ny,targetX,targetY) });
				}
			}
		}
		return -1;
	}
};

Bellman-Ford与SPFA优化

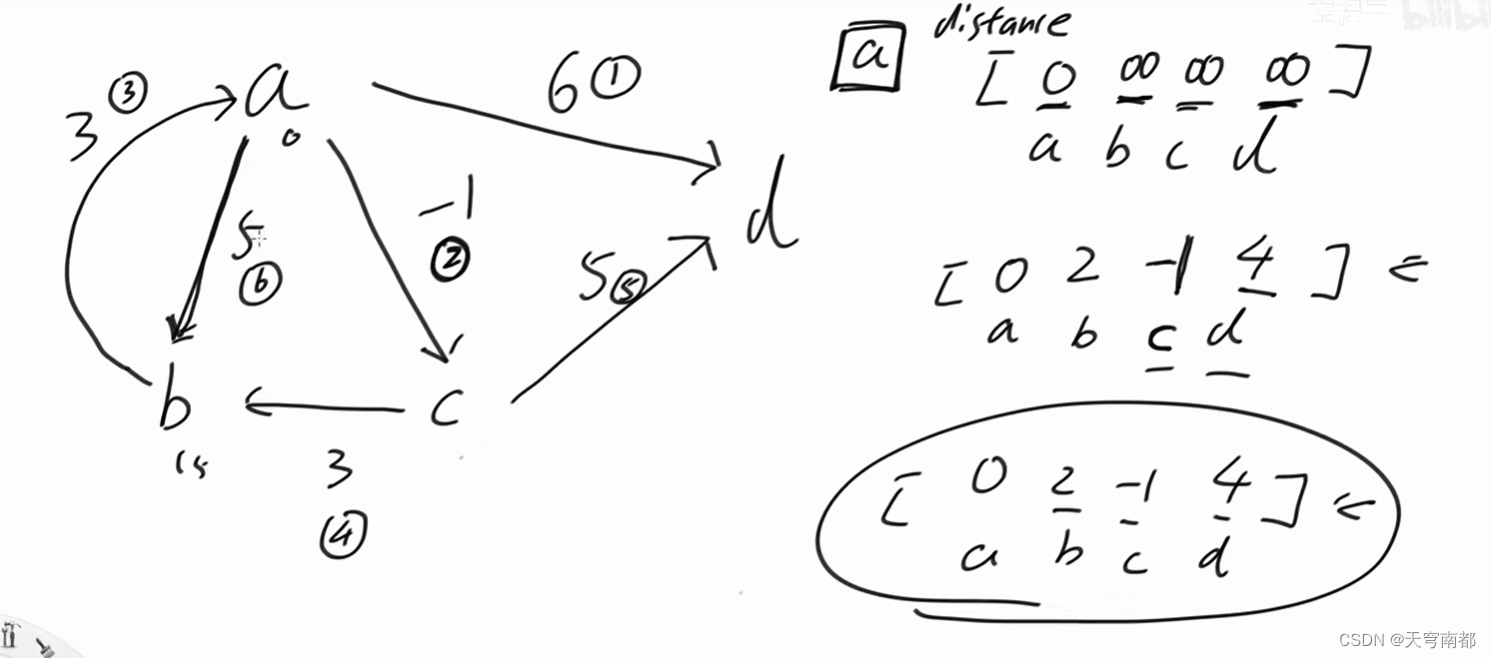
SPFA流程

洛谷模板

#include<iostream>
#include<cstdio>
#include<cmath>
#include<climits>
#include<cstring>

using namespace std;
const int N = 4e6 + 10;

struct edge {
    int v, w, ne;
}e[N];
int h[N]; int idx = 1;
int d[N], q[N];  //d[i]源点到节点距离的表 q[i]哪些节点被松弛了放入队列
bool st[N];  //节点是否在队列中
int cnt[N];  //节点被松弛次数
int l = 0, r = 0;

void add(int u, int v, int w) {
    e[idx] = { v,w,h[u] };
    h[u] = idx++;
}

bool  SPFA(int n) {
    d[1] = 0;
    cnt[1]++;
    q[r++] = 1;
    st[1] = true;
    while (l < r) {
        int u = q[l++];
        st[u] = false;
        //考察从u出发的所有边
        for (int i = h[u]; i > 0; i = e[i].ne) {
            int v = e[i].v;
            int w = e[i].w;
            if (d[u] + w < d[v]) {
                d[v] = d[u] + w;
                if (!st[v]) {
                    if (cnt[v]++ >= n)  //松弛次数为n 说明有负环
                        return true;
                    q[r++] = v;
                    st[v] = true;
                }
            }
        }
    }
    return false;
}

int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        l = r = 0;
        memset(e, 0, sizeof(e));
        memset(h, 0, sizeof(h));
        memset(cnt, 0, sizeof(cnt));
        memset(d, 0x7f, sizeof(d));
        memset(st, 0, sizeof(st));
        idx = 1;
        int n, m;
        scanf("%d%d", &n, &m);
        for (int i = 0; i < m; i++) {
            int u, v, w;
            scanf("%d%d%d", &u, &v, &w);
            add(u, v, w);
            if (w >= 0) {
                add(v, u, w);
            }
        }
        printf("%s", SPFA(n) ? "YES\n" : "NO\n");
    }
    return 0;
}

多源最短路

Floyd算法

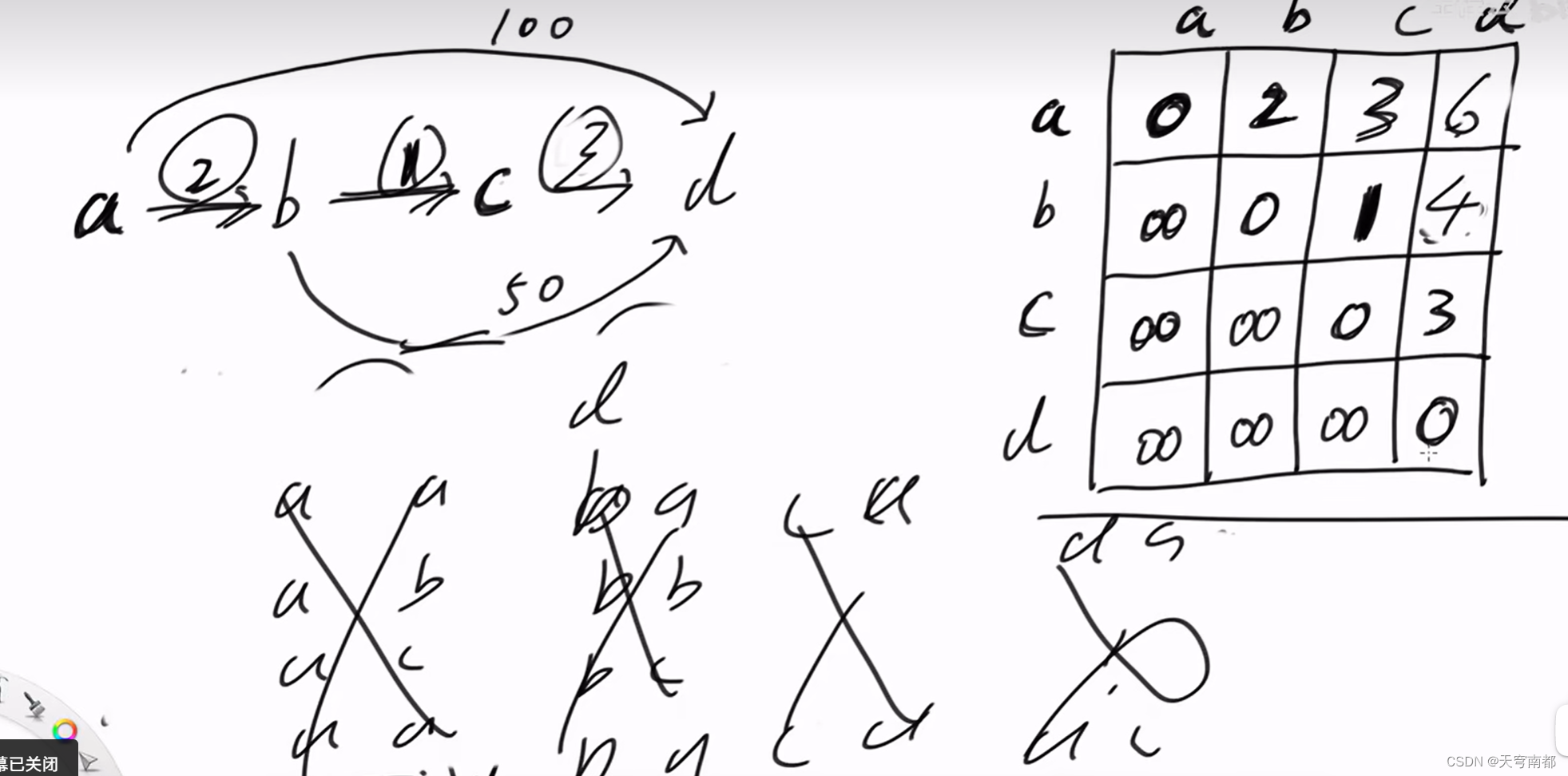
#include<iostream>
#include<cmath>
#include<climits>
using namespace std;
const int N = 111, M = 11111;
int d[N][N], path[M];
int n, m;

void floyed() {
	for (int k = 1; k <= n; k++) {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				d[i][j] = min(d[i][k] + d[k][j], d[i][j]);
			}
		}
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; i++) {
		scanf("%d", &path[i]);
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			d[i][j] = INT_MAX;
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			scanf("%d", &d[i][j]);
		}
	}
	floyed();
	int ans = 0;
	for (int i = 2; i <=m; i++) {
		ans += d[path[i - 1]][path[i]];
	}
	printf("%d", ans);
}