代码随想录算法训练营第四十八天|121. 买卖股票的最佳时机 122.买卖股票的最佳时机II

news2024/11/21 1:46:47

文档讲解：代码随想录

视频讲解：代码随想录B站账号

状态：看了视频题解和文章解析后做出来了

121. 买卖股票的最佳时机

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if len(prices) == 0:
            return 0
        dp = [[0] * 2 for _ in range(len(prices))]
        dp[0][0] -= prices[0]

        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i-1][0], -prices[i])
            dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0])

        return dp[-1][1]

时间复杂度：O(n)
空间复杂度：O(n)

1. 确定dp数组以及下标的含义

dp[i][0] : 我当前持有股票的时候所能拥有的最高现金，如果买入的话就是 - price[i]

dp[i][1]：我当前不持有股票所有拥有的最高现金。

2. 确定递推公式

（1）当前持有股票，我觉得这个就是在维护最小的买入价格。所以这个价格要取前一天持有股票时的现金和买入当前股票现金的较小值，就是决定哪一天买入价格最低，把这个最低的价格贯穿整个循环。dp[i][0] = max(dp[i-1][0], -prices[i])

（2）当前不持有股票。两种情况要么是持续上一天的不持有状态，要么是今天把股票卖了。dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])

3. dp数组的初始化

(1) 第0天持有股票，那肯定是买入，所以初始化为-prices[i]

(2) 第0天不持有股票，那就是什么也没干，初始化为0

4. 遍历顺序

递推公式中有i-1，所以从前往后遍历

5. dp数组举例

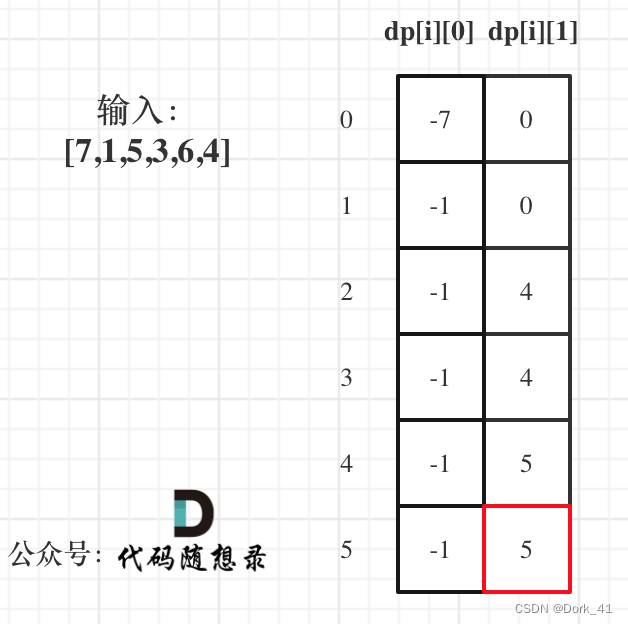
122.买卖股票的最佳时机II

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        dp = [[0] * 2 for _ in range(length)]
        dp[0][0] = -prices[0]
        dp[0][1] = 0
        for i in range(1, length):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]) #注意这里是和121. 买卖股票的最佳时机唯一不同的地方
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
        return dp[-1][1]