：状态
: 动作
: 奖励
: 奖励函数
: 非终结状态
: 全部状态，包括终结状态
: 动作集合
ℛ : 奖励集合
: 转移矩阵
: 离散时间步
： 回合内最终时间步
: 时间t的状态
: 时间t动作
: 时间t的奖励,通常为随机量，且由和决定
: 回报
: n步回报
: 
折扣回报
: 策略
: 根据确定性策略, 状态s时所采取的动作
: 根据随机性策略, 在状态s时执行动作a的概率
: 根据状态s和动作a，使得状态转移成
且获得奖励r的概率
: 根据转态s和动作a,使得状态转移成的概率
: 根据策略，状态s的价值(回报期望)
: 根据最优策略，状态s的价值
: 动作价值函数，根据策略，在状态s时执行动作a的价值
: 根据最优策略，在状态s时执行动作a的价值
: 状态价值函数的估计
: 动作价值函数的估计
： 
状态，动作，奖励的轨迹
： ![\gamma \in [0,1]](https://latex.csdn.net/eq?%5Cgamma%20%5Cin%20%5B0%2C1%5D)
, 奖励折扣因子
： 根据-贪婪策略，执行随机动作的概率
: 步长
: 资格迹的衰减速率
是轨迹的-折扣化回报，
是轨迹的概率：
，对于
是起始状态分布
,是起始状态分布
是策略的期望回报，![J(\pi)=\int_{\tau}p(\tau|\pi)R(\tau)=\mathbb{E}_{\tau\sim\pi}[R(\tau)]](https://latex.csdn.net/eq?J%28%5Cpi%29%3D%5Cint_%7B%5Ctau%7Dp%28%5Ctau%7C%5Cpi%29R%28%5Ctau%29%3D%5Cmathbb%7BE%7D_%7B%5Ctau%5Csim%5Cpi%7D%5BR%28%5Ctau%29%5D)
: 对于这个公式的理解为策略可以产生很多轨迹,产生每个轨迹的概率为
,而每个轨迹的奖励为,所以总的策略可以获得的奖励的期望就是所有轨迹的概率乘与该轨迹的奖励的积分。对于右边期望描述的就是对于服从策略的轨迹，求轨迹的奖励值的期望。
是最优策略，最优策略就是能够获得最大的策略期望的策略，即为
是状态s在策略下的价值，也就是这个状态能够获得的期望回报。
是状态s在最优策略下的价值，也就是这个状态能够在最优策略下获得的期望回报，最终都转化为了奖励的计算。
是状态s在策略下执行动作a的价值（期望回报）
是状态s在最优策略下执行动作a的价值（期望回报）
是对MRP（Markov Reward Process）中从状态s开始的状态价值的估计
是对MDP（Markov Decision Process）中在线状态价值函数的估计，给定策略,有期望回报：
![V^{\pi}(s)\approx v_{\pi}(s)=\mathbb{E}_{\tau\sim\pi}[R(\tau)|S_0=s]](https://latex.csdn.net/eq?V%5E%7B%5Cpi%7D%28s%29%5Capprox%20v_%7B%5Cpi%7D%28s%29%3D%5Cmathbb%7BE%7D_%7B%5Ctau%5Csim%5Cpi%7D%5BR%28%5Ctau%29%7CS_0%3Ds%5D)
其中MP，MRP，MDP参考：MP、MRP、MDP（第二节） - 知乎 (zhihu.com)
是对MDP下在线动作价值函数的估计，给定策略 ，有期望回报：
![Q^{\pi}(s,a)\approx q_{\pi}(s,a)=\mathbb{E}_{\tau\sim\pi}[R(\tau)|S_0=s,A_0=a]](https://latex.csdn.net/eq?Q%5E%7B%5Cpi%7D%28s%2Ca%29%5Capprox%20q_%7B%5Cpi%7D%28s%2Ca%29%3D%5Cmathbb%7BE%7D_%7B%5Ctau%5Csim%5Cpi%7D%5BR%28%5Ctau%29%7CS_0%3Ds%2CA_0%3Da%5D)
是对MDP下最优动作价值函数的估计，根据最优策略，有期望回报：
![V^{\star}(s)\approx v_{\star}(s) = max_{\pi}\mathbb{E}_{\tau\sim\pi}[R(\tau)|S_0=s]](https://latex.csdn.net/eq?V%5E%7B%5Cstar%7D%28s%29%5Capprox%20v_%7B%5Cstar%7D%28s%29%20%3D%20max_%7B%5Cpi%7D%5Cmathbb%7BE%7D_%7B%5Ctau%5Csim%5Cpi%7D%5BR%28%5Ctau%29%7CS_0%3Ds%5D)
是对MDP下最优动作价值函数的估计，根据最优策略，有期望回报：
![Q^{\star}(s,a)\approx q_{\star}(s,a) = max_{\pi}\mathbb{E}_{\tau \sim\pi}[R(\tau)|S_0=s,A_0=a]](https://latex.csdn.net/eq?Q%5E%7B%5Cstar%7D%28s%2Ca%29%5Capprox%20q_%7B%5Cstar%7D%28s%2Ca%29%20%3D%20max_%7B%5Cpi%7D%5Cmathbb%7BE%7D_%7B%5Ctau%20%5Csim%5Cpi%7D%5BR%28%5Ctau%29%7CS_0%3Ds%2CA_0%3Da%5D)
是对状态s和动作a的优势估计函数：
在线状态价值函数和在线动作价值函数的关系：
![v_{\pi}(s)=\mathbb{E}_{a\sim\pi}[q_{\pi}(s,a)]](https://latex.csdn.net/eq?v_%7B%5Cpi%7D%28s%29%3D%5Cmathbb%7BE%7D_%7Ba%5Csim%5Cpi%7D%5Bq_%7B%5Cpi%7D%28s%2Ca%29%5D)
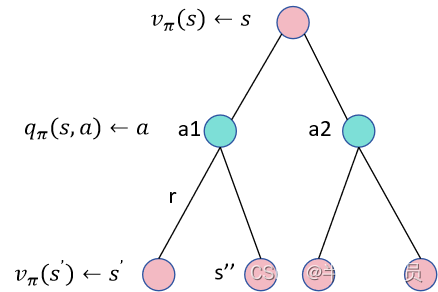
如上图所示：状态s对应多个动作a1,a2，执行一个动作之后，又可能转移到多个状态中去， 所以的值就是在状态s之下能够采取的所有动作的动作价值函数的期望，即为
另一种写法：
这里写的是和之间的关系，同理另外一种转换关系是，执行一个动作之后得到的及时奖励值+下一个状态的状态价值函数的折扣，即为
,
是在状态s执行动作a转移到s'的概率，这样就把和
关联起来了。另一种写法如下：
![v_{\pi}(s)=\mathbb{E}_{a\sim \pi(\cdot |s),s'\sim p(\cdot |s,a)}[R(s,a)+\gamma v_{\pi}(s')]](https://latex.csdn.net/eq?v_%7B%5Cpi%7D%28s%29%3D%5Cmathbb%7BE%7D_%7Ba%5Csim%20%5Cpi%28%5Ccdot%20%7Cs%29%2Cs%27%5Csim%20p%28%5Ccdot%20%7Cs%2Ca%29%7D%5BR%28s%2Ca%29+%5Cgamma%20v_%7B%5Cpi%7D%28s%27%29%5D)
最优状态价值函数和最优动作价值函数的关系是：
上面的公式很好理解，在最优策略下，给一个状态s，这个策略肯定能够选到最好的动作去执行，那么当前状态的价值函数就不是去求所有动作价值函数的期望了，而是就等于动作价值函数最大的那个值。
是在最优策略下，状态s执行的最优动作
在线动作价值函数的贝尔曼方程：
![q_{\pi}(s,a)=\mathbb{E}_{s' \sim p(\cdot |s,a)}[R(s,a)+\gamma\mathbb{E}_{a' \sim \pi(\cdot|s')}[q_{\pi}(s',a')]]](https://latex.csdn.net/eq?q_%7B%5Cpi%7D%28s%2Ca%29%3D%5Cmathbb%7BE%7D_%7Bs%27%20%5Csim%20p%28%5Ccdot%20%7Cs%2Ca%29%7D%5BR%28s%2Ca%29+%5Cgamma%5Cmathbb%7BE%7D_%7Ba%27%20%5Csim%20%5Cpi%28%5Ccdot%7Cs%27%29%7D%5Bq_%7B%5Cpi%7D%28s%27%2Ca%27%29%5D%5D)
另外一种写法是：
上面是 和
的关系，下面是和的关系：
另外一种写法是：
![q_{\pi}(s,a)=R_s^a+\gamma\mathbb{E}_{s' \sim p(\cdot|s,a)}[v_{\pi}(s')]](https://latex.csdn.net/eq?q_%7B%5Cpi%7D%28s%2Ca%29%3DR_s%5Ea+%5Cgamma%5Cmathbb%7BE%7D_%7Bs%27%20%5Csim%20p%28%5Ccdot%7Cs%2Ca%29%7D%5Bv_%7B%5Cpi%7D%28s%27%29%5D)
最优状态价值函数的贝尔曼方程：
![v_{\star}(s)=max_a \mathbb{E}_{s' \sim p(\cdot | s,a)}[R(s,a)+\gamma v_{\star}(s')]](https://latex.csdn.net/eq?v_%7B%5Cstar%7D%28s%29%3Dmax_a%20%5Cmathbb%7BE%7D_%7Bs%27%20%5Csim%20p%28%5Ccdot%20%7C%20s%2Ca%29%7D%5BR%28s%2Ca%29+%5Cgamma%20v_%7B%5Cstar%7D%28s%27%29%5D)
另外一种写法是：
最优动作价值函数的贝尔曼方程：
![q_{\star}(s,a)=\mathbb{E}_{s' \sim p(\cdot |s,a)}[R(s,a)+\gamma max_{a'}q_{\star}(s',a')]](https://latex.csdn.net/eq?q_%7B%5Cstar%7D%28s%2Ca%29%3D%5Cmathbb%7BE%7D_%7Bs%27%20%5Csim%20p%28%5Ccdot%20%7Cs%2Ca%29%7D%5BR%28s%2Ca%29+%5Cgamma%20max_%7Ba%27%7Dq_%7B%5Cstar%7D%28s%27%2Ca%27%29%5D)
另外一种写法是：
![[C国演义] 第二十一章](https://img-blog.csdnimg.cn/890cbfc2fc244fe8afd95745dca4f7b3.png)
