257. 二叉树的所有路径 - 力扣（LeetCode）

对于二叉树的深度搜索，要学会从以下三个角度来去看待问题：

1. 全局变量，有时候全局变量会减少参数的个数，简化很多流程；

这道题目，要返回根结点到叶子节点的多条路径，此处就考虑用全局变量来存储每一条路径；

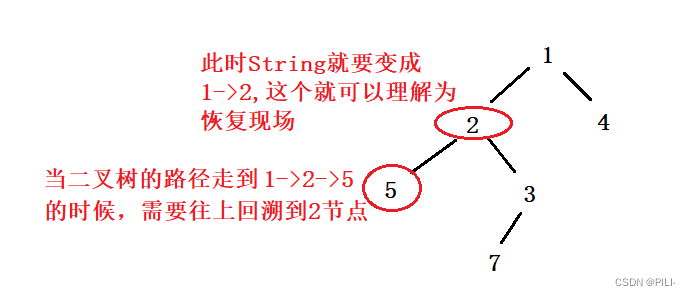
2. 回溯，基本上深度搜索就会涉及到回溯，而对于回溯，就要联想到 "恢复现场" ;

从这道题的角度出发，理解恢复现场：

3. 剪枝，为了让程序的运行效率进一步提高；

这道题目的剪枝可以用在：判断左子树或者右子树是否为空，为空的话就不再进入递归了；

代码实现 

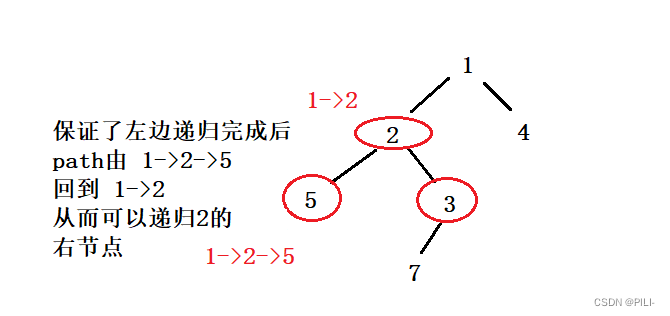
结合下述代码来理解，StringBuffer path = new StringBuffer(_path); 这条语句涉及到值传递的相关知识，这里不做过多解释了，该语句实现了恢复现场，让 dfs(root.left,path); 递归完成后，要进行下一句 dfs(root.right,path); 的时候，path 依旧是当前层次的 path；

class Solution {
    List<String> str = new ArrayList<>();
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root,new StringBuffer());
        return str;
    }
    public void dfs(TreeNode root,StringBuffer _path){
        StringBuffer path = new StringBuffer(_path);    // 实现了恢复现场

        path.append(Integer.toString(root.val));
        if(root.left == null && root.right == null){
            str.add(path.toString());   // 如果左右节点都没了，该节点就是叶子节点了，就可以存入数组了
        }else{
            // 如果不是叶子节点
            path.append("->");
        }
        // 剪枝:左子树不为空，就继续递归
        if(root.left != null) dfs(root.left,path);      // 递归left
        // 剪枝:右子树不为空，就继续递归
        if(root.right != null) dfs(root.right,path);    // 递归right
    }
}