一、(what?)
二、(why?)
三、(how?)
四、典型例题分析:
例题1:大卖场购物车2——0-1背包问题

问题分析:

算法设计:

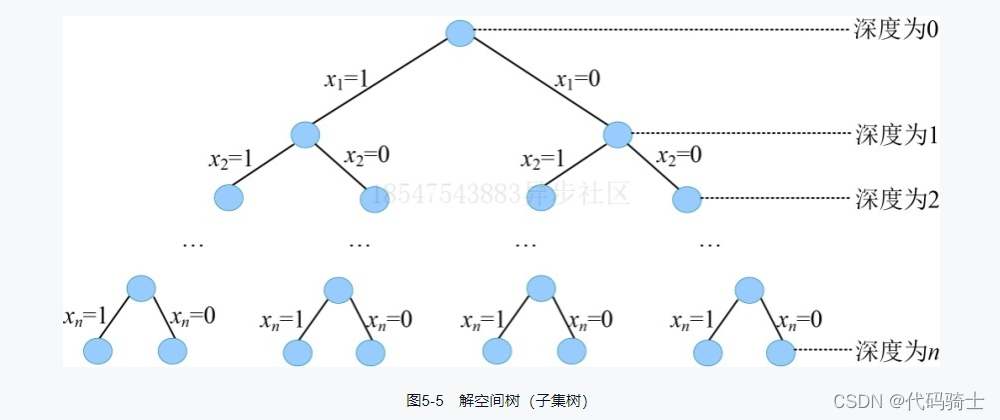

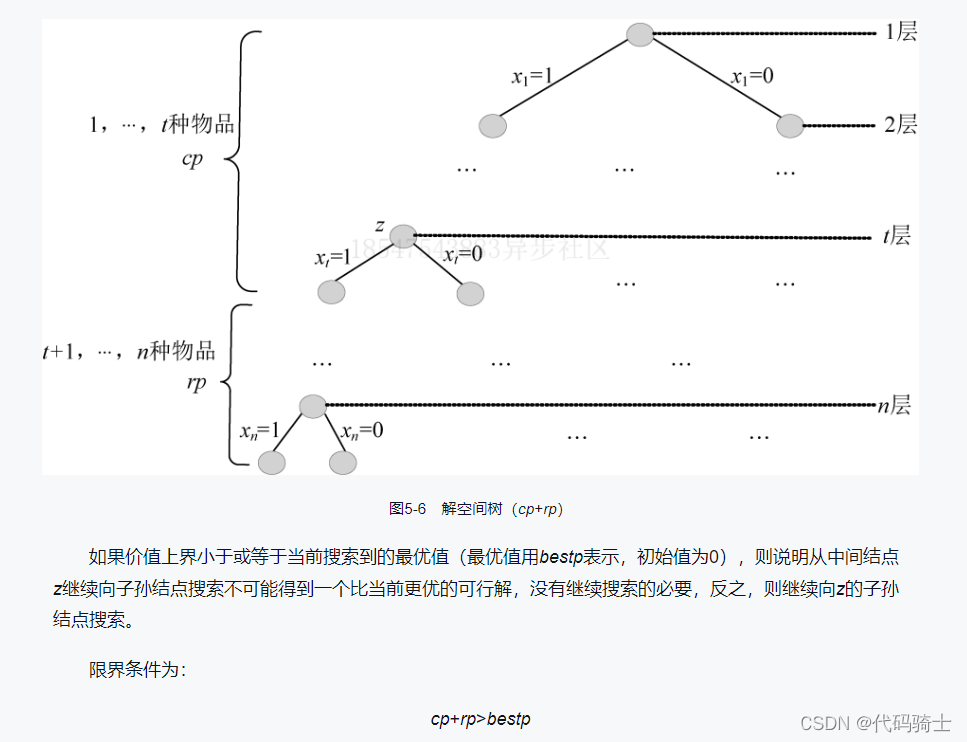

图解算法:
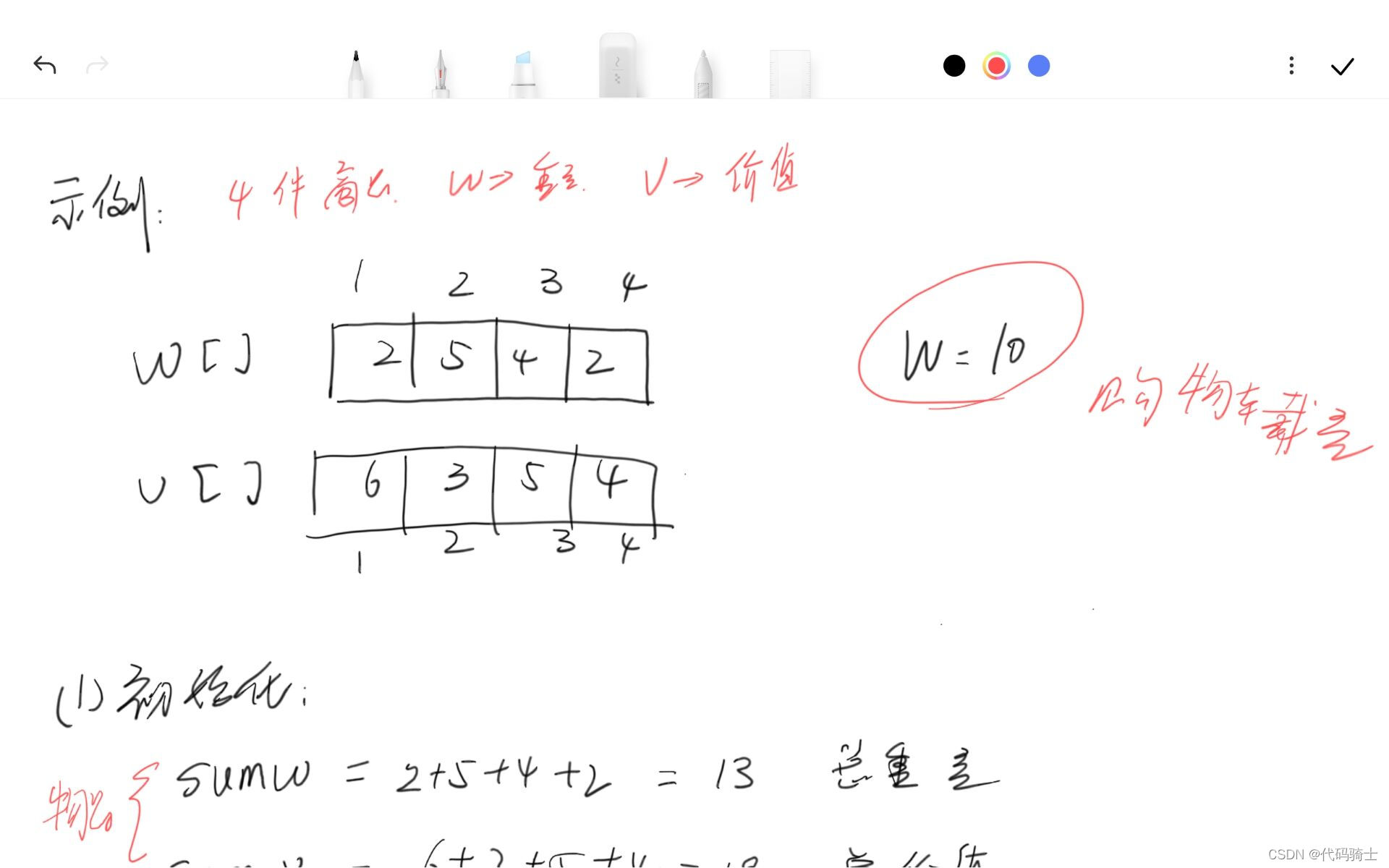




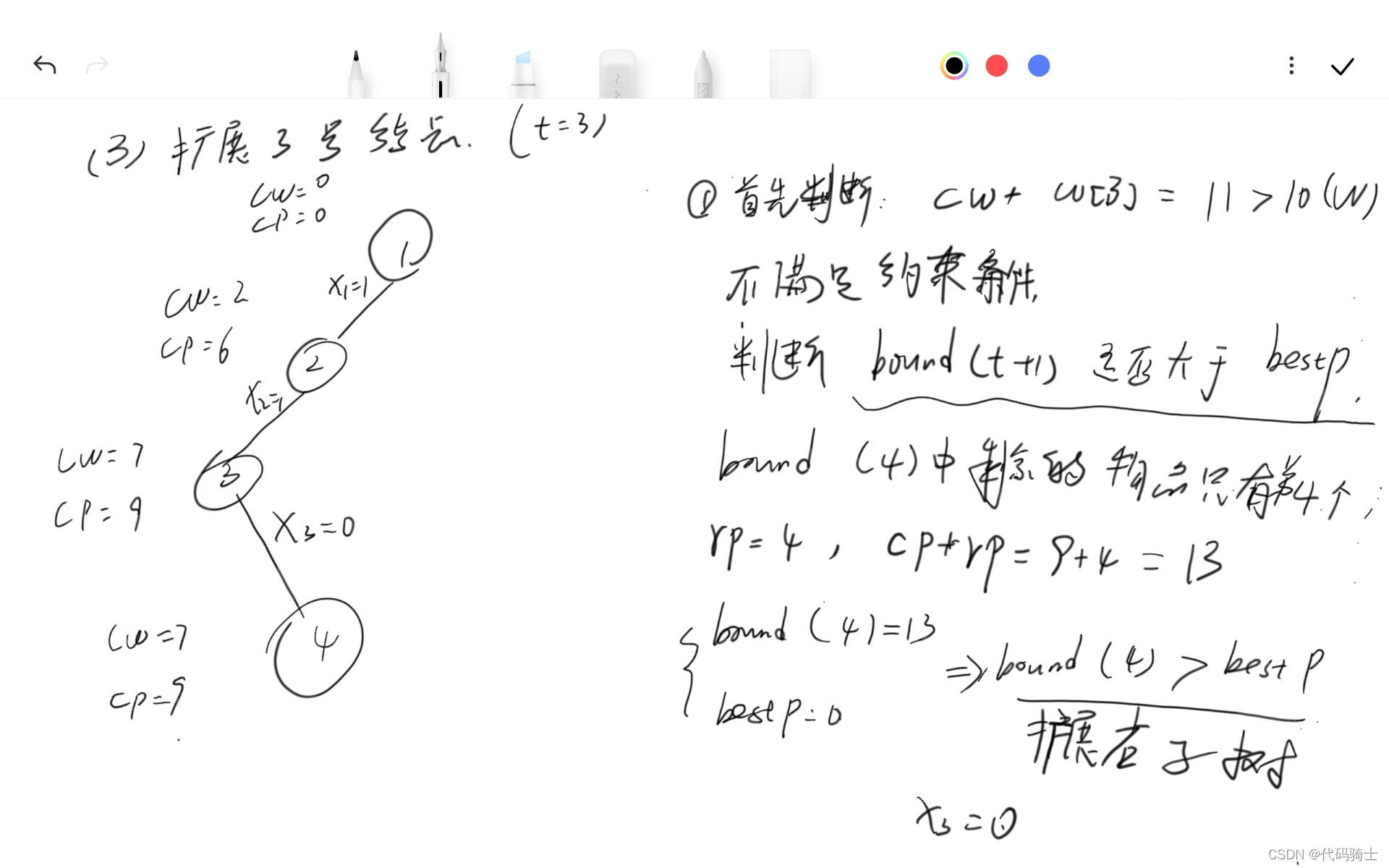
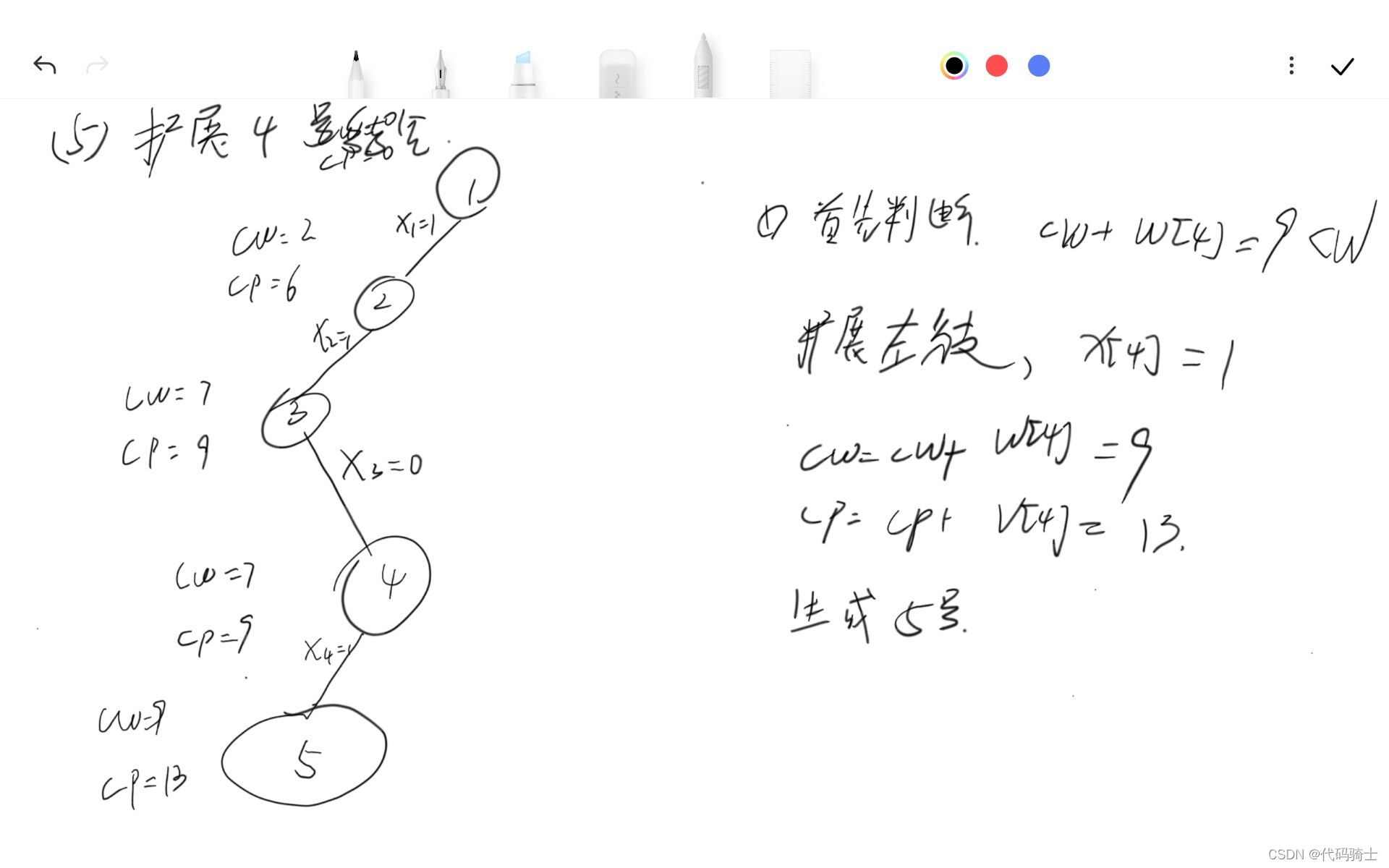
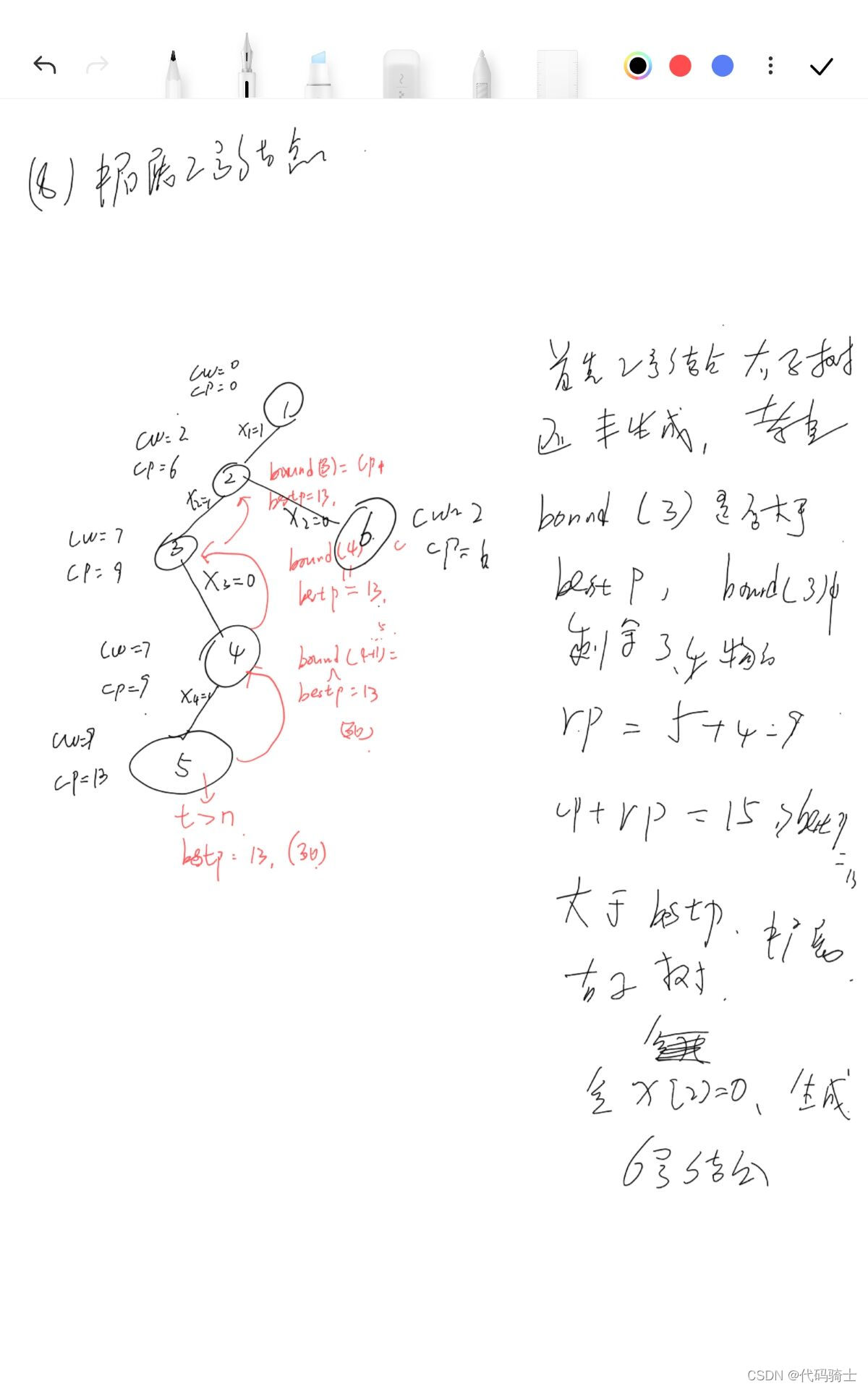


伪代码:

double Bound(int i)//计算上界(即已装入物品价值+剩余物品的总价值)
{
int rp=0; //剩余物品为第i~n种物品
while(i<=n)//依次计算剩余物品的价值
{
rp+=v[i];
i++;
}
return cp+rp;//返回上界
} 
void Backtrack(int t) //t表示当前扩展结点在第t层
{
if(t>n) //已经到达叶子结点
{
for(j=1;j<=n;j++)
{
bestx[j]=x[j];
}
bestp=cp; //保存当前最优解
return ;
}
if(cw+w[t]<=W) //如果满足约束条件则搜索左子树
{
x[t]=1;
cw+=w[t];
cp+=v[t];
Backtrack(t+1);
cw-=w[t];
cp-=v[t];
}
if(Bound(t+1)>bestp) //如果满足限界条件则搜索右子树
{
x[t]=0;
Backtrack(t+1);
}
} 完整代码:
#include<iostream>
#include<string>
#include<algorithm>
#define M 105
using namespace std;
int i,j,n,W; //n表示n个物品,W表示购物车的容量
double w[M],v[M];//w[i] 表示第i个物品的重量,v[i] 表示第i个物品的价值
bool x[M]; //x[i]表示第i个物品是否放入购物车
double cw; //当前重量
double cp;//当前价值
double bestp;//当前最优价值
bool bestx[M]; //当前最优解
double Bound(int i)//计算上界(即已装入物品价值,剩余物品的总价值)
{
int rp=0;//剩余物品为第i~n种物品
while(i<=n)//一次计算剩余物品的价值
{
rp+=v[i];
i++;
}
return cp+rp;//返回上界
}
void Backtrack(int t)//t表示当前扩展点在第t层
{
if(t>n)//已经到达叶子结点
{
for(j=1;j<=n;j++)
{
bestx[j]=x[j];
}
bestp=cp;//保存当前最优解
return ;
}
if(cw+w[i]<=W)//如果满足条件约束搜索左子树
{
x[t]=1;
cw+=w[t];
cp+=v[t];
Backtrack(t+1);
cw-=w[t];
cp-=v[t];
}
if(Bound(t+1)>bestp)//如果满足限界条件搜索右子树
{
x[t]=0;
Backtrack(t+1);
}
}
void Knapsack(double W,int n)
{
//初始化
cw=0;
cp=0;
bestp=0;
double sumw=0.0;
double sumv=0.0;
for(i=1;i<=n;i++)
{
sumv+=v[i];
sumw+=w[i];
}
if(sumw<=W)
{
bestp=sumv;
cout<<"放入购物车的物品最大价值为:"<<bestp<<endl;
cout<<"所有的物品均放入购物车。";
return;
}
Backtrack(1);
cout<<"放入购物车的物品最大价值为:"<<bestp<<endl;
cout<<"放入购物车的物品序号为:";
for(i=1;i<=n;i++) //输出最优解
{
if(bestx[i]==1)
cout<<i<<" ";
}
cout<<endl;
}
int main()
{
cout << "请输入物品的个数n:";
cin >> n;
cout << "请输入购物车的容量W:";
cin >> W;
cout << "请依次输入每个物品的重量w和价值v,用空格分开:";
for(i=1;i<=n;i++)
cin>>w[i]>>v[i];
Knapsack(W,n);
return 0;
}
例题2:
例题3:
例题4:
例题5:
例题6: