一、(what?)
二、(why?)
三、(how?)
四、典型例题分析:
例题1:神奇的兔子序列

输入:月数
输出:兔子数
思路:


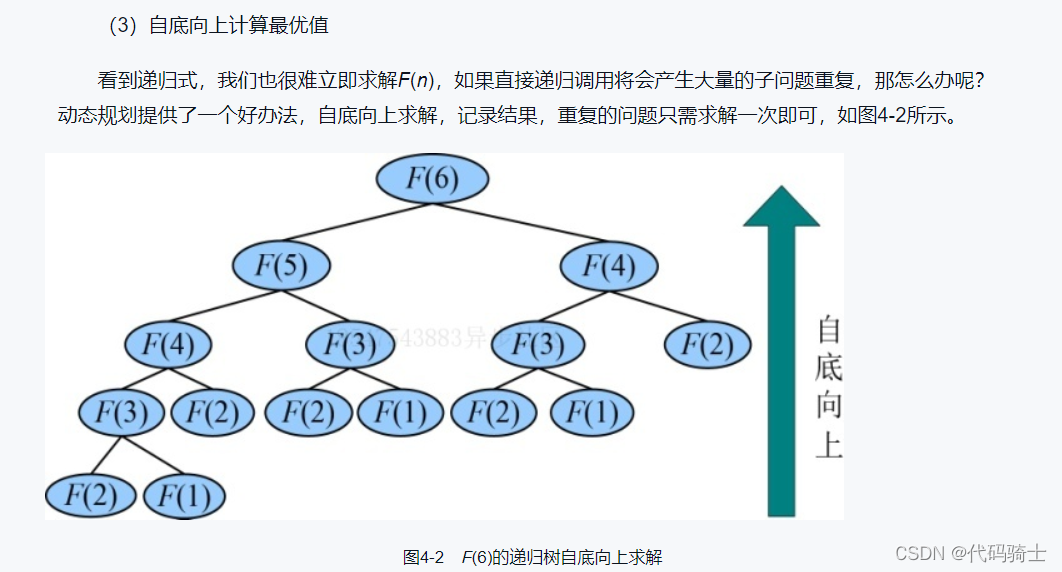
代码1(函数递归):
#include<iostream>
using namespace std;
int fib(int n)
{
if(n < 1)
return -1;
else if(n == 1|| n == 2)
return 1;
else
return fib(n-1)+fib(n-2);
}
int main()
{
int n;
cin>>n;
cout<<fib(n);
return 0;
} 代码2(数组递归):
#include<iostream>
using namespace std;
int fib(int n)
{
if(n < 1) return -1;
int F[n+1];
F[1] = 1, F[2] = 1;
for(int i = 3; i <= n; i++)
F[i] = F[i-1]+F[i-2];
return F[n];
}
int main()
{
int n;
cin>>n;
cout<<fib(n);
return 0;
} 例题2:孩子有多像爸爸——最长公共子序列
 暴力搜索
暴力搜索
举个简单的暴力搜索的
#include<iostream>
using namespace std;
int main()
{
char s[7]={'A','B','C','B','A','D','B'};
for(int k=0;k<=7;k++)
{
for(int i=k;i<=7;i++)
{
for(int j=k;j<i;j++)
{
cout<<s[j];
}
cout<<endl;
}
}
return 0;
} 显示所有子串:
求其中一个子串的数组:
#include<iostream>
using namespace std;
int main()
{
char s[7] = {'A','B','C','B','A','D','B'};
//char ss[6] = {'B','C','B','A','A','C'};
string str1[100],str2[100];
int len1=0,len2=0;
for(int k=0;k<=7;k++)
{
for(int i=k;i<=7;i++)
{
for(int q=k;q<i;q++)
{
str1[len1]+=s[q];
}
len1++;
}
}
for(int k=0;k<len1;k++)
{
cout<<str1[k]<<endl;
}
return 0;
} 输出:

题解代码:
#include<iostream>
#include<string>
using namespace std;
const int MAX=1000;
char s[MAX],ss[MAX];
string str1[MAX],str2[MAX];
int len1=0,len2=0;
int main()
{
//char s[7] = {'A','B','C','B','A','D','B'};
//char ss[6] = {'B','C','B','A','A','C'};
//string str1[100],str2[100];
//int len1=0,len2=0;
string st1,st2;
cin>>st1>>st2;
int i=0,j=0;
while(i<st1.length())
{
s[i]=st1[i];
i++;
}
while(j<st2.length())
{
ss[j]=st2[j];
j++;
}
//存入第一个子串数组
for(int k=0;k<=7;k++)
{
for(int i=k;i<=7;i++)
{
for(int q=k;q<i;q++)
{
str1[len1]+=s[q];
}
len1++;
}
}
/*
for(int k=0;k<len1;k++)
{
cout<<str1[k]<<endl;
} */
//存入第二个子串数组
for(int k=0;k<=6;k++)
{
for(int i=k;i<=6;i++)
{
for(int q=k;q<i;q++)
{
str2[len2]+=ss[q];
}
len2++;
}
}
/*
for(int k=0;k<len2;k++)
{
cout<<str2[k]<<endl;
}
*/
int temp=0,max=-1000;
string answer;
for(int i=0;i<len1;i++)
{
string strr1=str1[i];
for(int j=0;j<len2;j++)
{
if(str2[j]==strr1)
{
temp=strr1.length();
if(temp>=max)
{
max=temp;
answer=strr1;
}
}
}
}
cout<<answer<<endl<<max;
return 0;
} 结果:
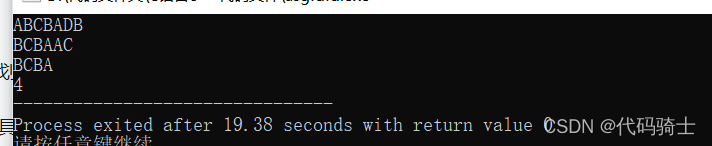
*注:这并不是例题的解法,只是对暴力搜索举个例子,二者并无关联!
原理题的条件子串是从父亲的基因中取一些值并非一定连续!!!
下面,用动态规划算法解决此问题
算法设计:

图解算法:
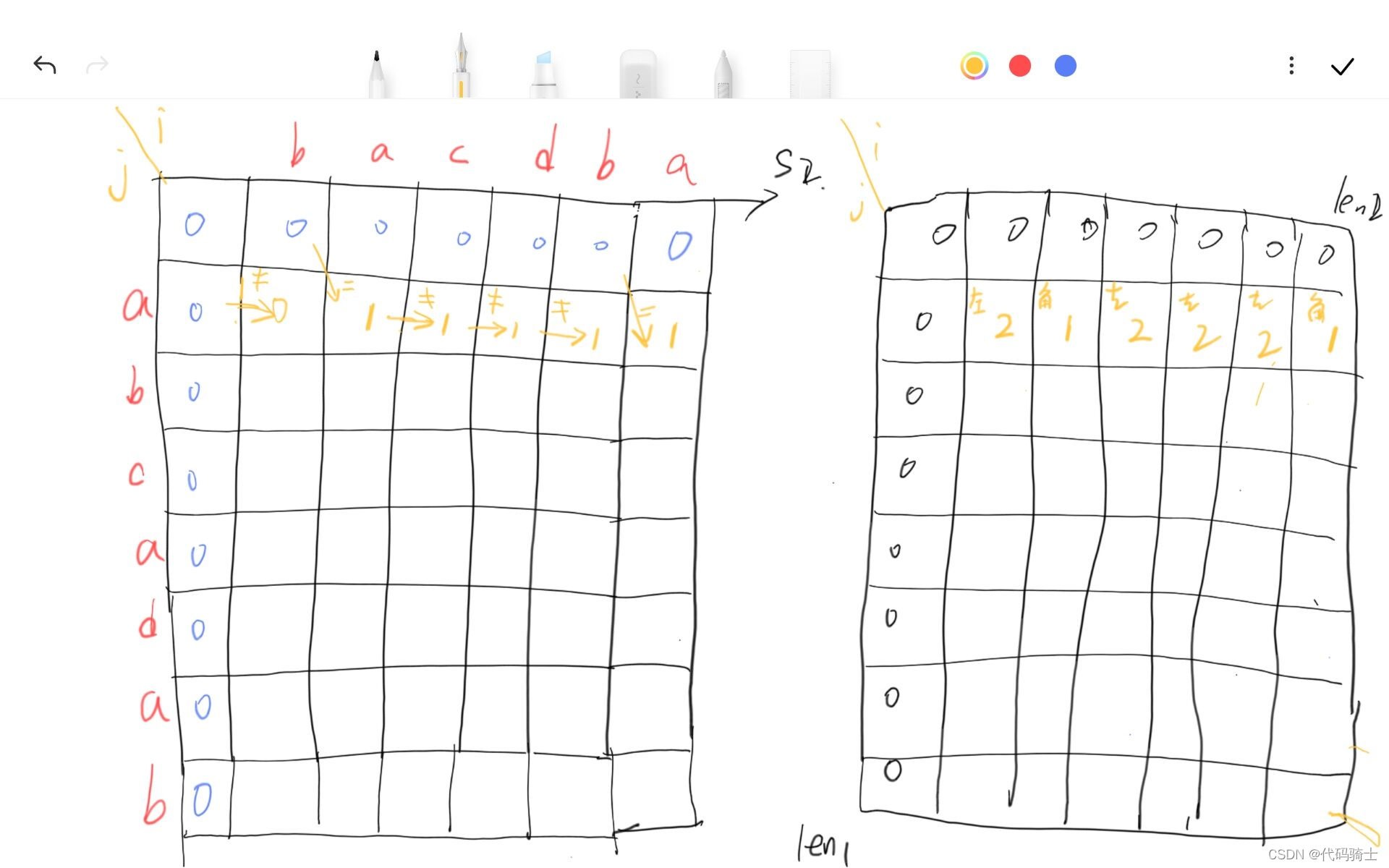

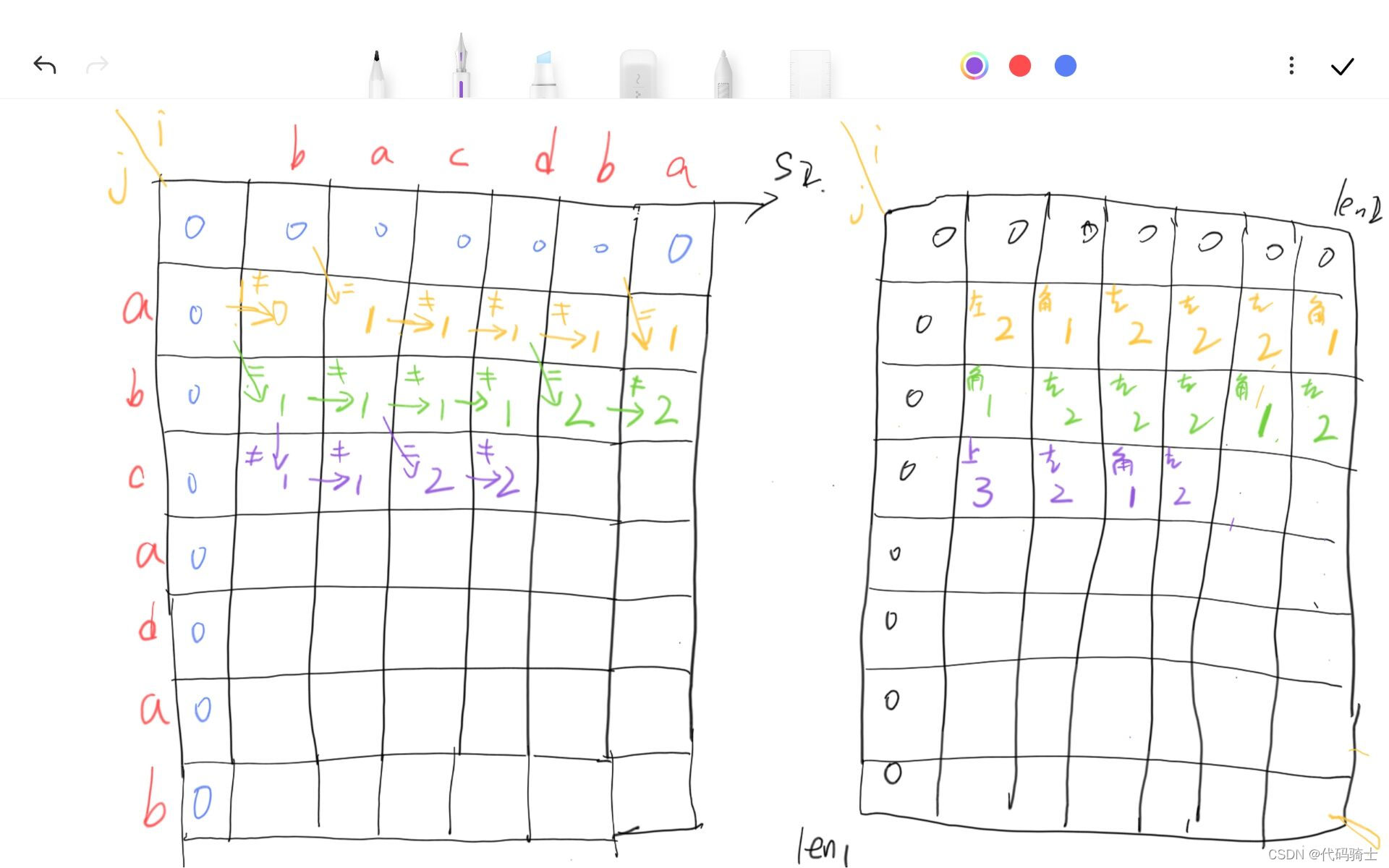


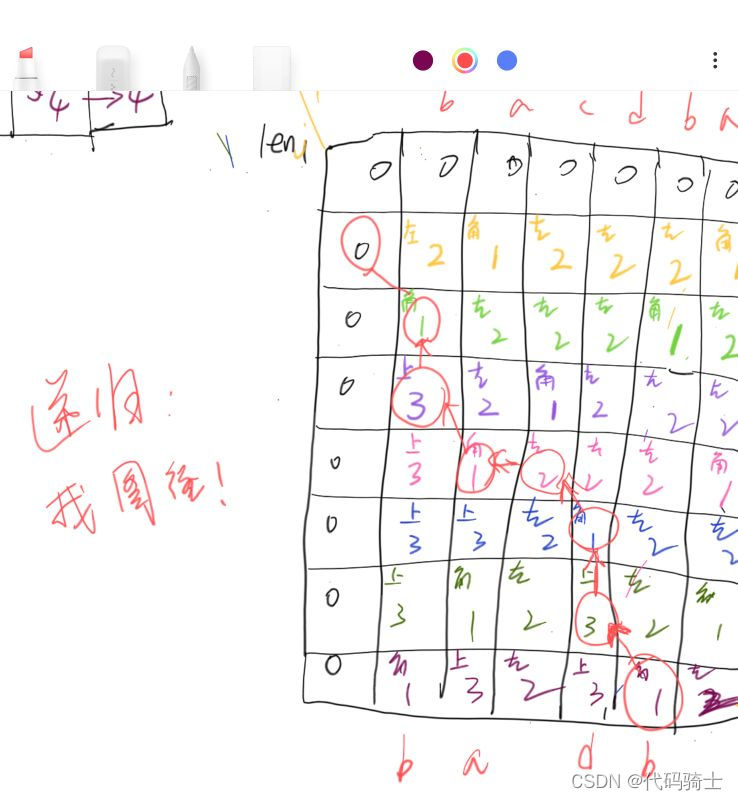
伪代码:

Void LCSL()
{
int I,j;
for(I = 1;I <= len1;i++) //控制s1序列
for(j = 1;j <= len2;j++) //控制s2序列
{
if(s1[i-1]==s2[j-1]) //字符下标从0开始
{ //如果当前字符相同,则公共子序列的长度为该字符前的最长公共序列+1
c[i][j] = c[i-1][j-1]+1;
b[i][j] = 1;
}
else
{
if(c[i][j-1]>=c[i-1][j]) //两者找最大值,并记录最优策略来源
{
c[i][j] = c[i][j-1];
b[i][j] = 2;
}
else
{
c[i][j] = c[i-1][j];
b[i][j] = 3;
}
}
}
}
Void print(int I, int j)//根据记录下来的信息构造最长公共子序列(从b[i][j]开始递推)
{
if(i==0 || j==0) return;
if(b[i][j]==1)
{
print(i-1,j-1);
cout<<s1[i-1];
}
else if(b[i][j]==2)
print(I,j-1);
else print(i-1,j);
}代码:
#include<iostream>
#include<string>
using namespace std;
const int N = 1002;//数组最大长度
int c[N][N], b[N][N];//c:公共子序列长度。b:答案路径
char s1[N], s2[N];
int len1, len2;
//动态规划查询最大子序列函数
void LCSL()
{
int i, j;
for (i = 1; i <= len1; i++)//控制s1序列
{
for (j = 1; j <= len2; j++)//控制s2序列
{
//动态规划开始
if (s1[i - 1] == s2[j - 1])//字符下标从0开始
{//如果字符相同,公共子序列的长度为该字符前的最长公共子序列(左上角)+1
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = 1;//此情况标记为1
}
else
{//如果字符不相等的子序列长度
if (c[i][j - 1] >= c[i - 1][j])
{//如果上面的大于左面,子序列长度为上值
c[i][j] = c[i][j - 1];
b[i][j] = 2;//取上值为2
}
else
{//如果左大于上,取左值
c[i][j] = c[i - 1][j];
b[i][j] = 3;//取左值为3
}
}
}
}
for (i = 0; i <= len1; i++)
{
for(j = 0; j <= len2; j++)
{
cout << c[i][j];
}
cout << endl;
}
}
//输出最优路径的函数(因为是函数递归,所以经过倒退能得到正序路径)
void print(int i, int j)//从b[i][j]开始递推
{
if (i == 0 || j == 0) return;//如果有一个序列递归完了就结束递归
if (b[i][j] == 1)
{//说明此时s1[i-1]=s2[j-1],b[i][j]的值来自c左上角
print(i - 1, j - 1);//递归去左上角
cout << s1[i - 1];
}
else if (b[i][j] == 2)
{//s1[i-1]与s2[j-1]不等,b[i][j]值来自c上
print(i, j - 1);
}
else
{//字符不等取值来自左
print(i - 1, j);
}
}
int main()
{
int i, j;
cout << "输入字符串s1:" << endl;
cin >> s1;
cout << "输入字符串s2:" << endl;
cin >> s2;
len1 = strlen(s1);//求char型数组的长度
len2 = strlen(s2);
for (i = 0; i <= len1; i++)
{
c[i][0] = 0;//初始化第一行
}
for (j = 0; j <= len2; j++)
{
c[0][j] = 0;//初始化第一列
}
LCSL();//求最长子序列
cout << "最长子序列长度为:" << c[len1][len2] << endl;
cout << "最长公共子序列是:";
print(len1, len2);
return 0;
}输出:
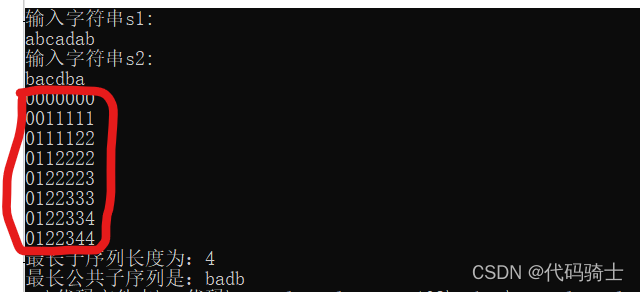
例题3:DNA基因鉴定——编辑距离

算法设计:

算法图解:
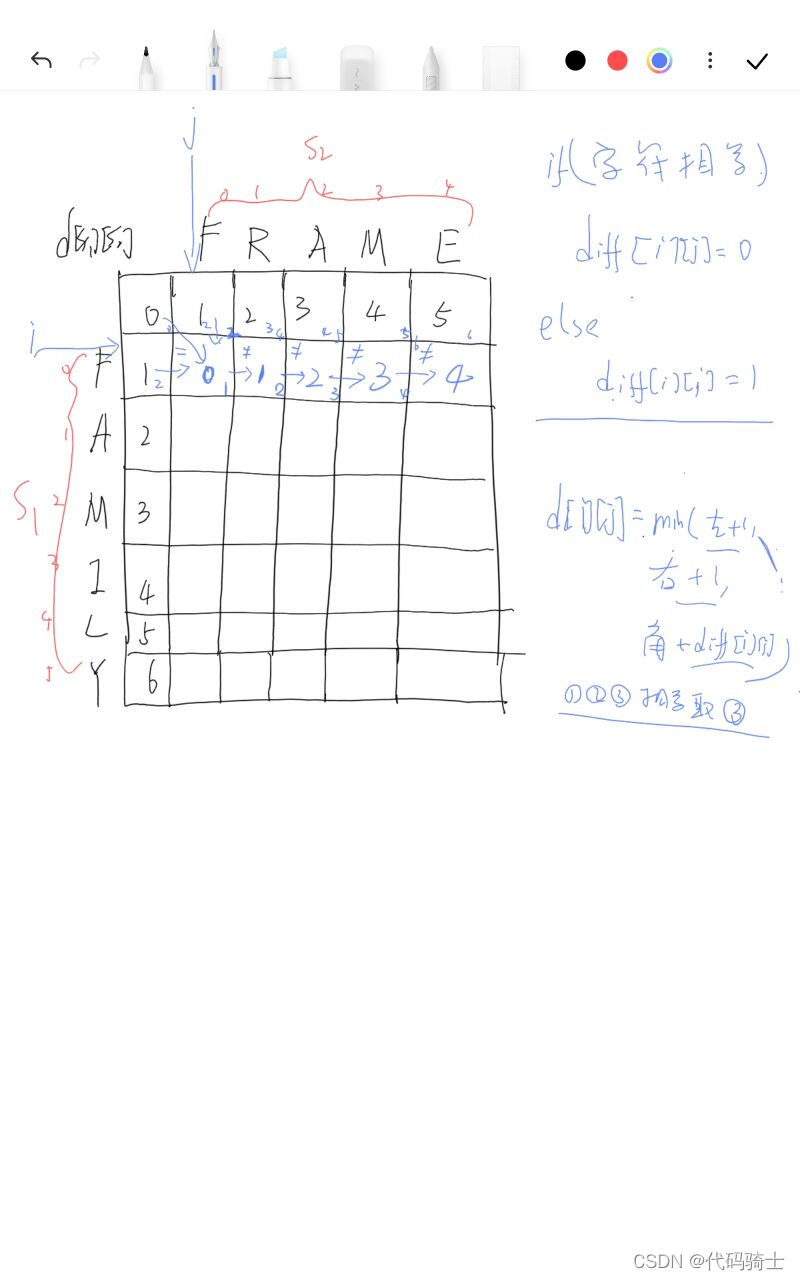


伪代码:

int editdistance(char *str1, char *str2)
{
int len1 = strlen(str1); //计算字符串长度
int len2 = strlen(str2);
for(int i=0;i<=len1;i++) //当第二个串长度为0,编辑距离初始化为i
d[i][0]= i;
for(int j=0;j<=len2;j++) //当第一个串长度为0,编辑距离初始化为j
d[0][j]=j;
for(int i=1;i <=len1;i++) //遍历两个字符串
{
for(int j=1;j<=len2;j++)
{
int diff;//判断str[i]是否等于str2[j],相等为0,不相等为1
if(str1[i-1] == str2[j-1]) //相等
diff = 0 ;
else
diff = 1 ;
int temp = min(d[i-1][j] + 1, d[i][j-1] + 1);//先两者取最小值
d[i][j] = min(temp, d[i-1][j-1] + diff);//再取最小值,
//相当于三者取最小值d[i-1][j] + 1, d[i][j-1] + 1,d[i-1][j-1] + diff
}
}
return d[len1][len2];
}完整代码:
#include<iostream>
#include<string>
using namespace std;
const int N = 100;
char str1[N],str2[N];
int d[N][N];//d[i][j]表示的str1前i个字符的str2前j个字符的编辑距离
int StrLen(char *s)//求字符串长度
{
int i=0;
while(s[i]!='\0')
{
i++;
}
return i;
}
int min(int a,int b)
{
return a<b?a:b; //返回较小值
}
int editdistance(char *str1,char *str2)
{
int len1=StrLen(str1);
int len2=StrLen(str2);
//初始化
for(int i=0;i<=len1;i++)
{//第二个串长度为0,编辑距离初始化为i
d[i][0] = i;
}
for(int j=0;j<=len2;j++)
{//第二个串长度为0,编辑距离初始化为j
d[0][j] = j;
}
//遍历两个字符串
for(int i=1;i<=len1;i++)
{
for(int j=1; j<=len2;j++)
{
int diff;//判断字符是否相等,相等不需要编辑+0,不相等+1
if(str1[i-1] == str2[j-1])
{
diff=0;
}
else
{
diff=1;
}
int temp=min(d[i-1][j]+1,d[i][j-1]+1);
d[i][j] = min(temp,d[i-1][j-1]+diff);//连去两次两个求最小值等价于三个求最小值
}
}
for(int i=0;i<=len1;i++)
{
for(int j=0;j<=len2;j++)
{
cout<<d[i][j];
}
cout<<endl;
}
return d[len1][len2];
}
int main()
{
cin>>str1>>str2;
cout<<editdistance(str1,str2);
return 0;
}
输入输出:
例题4:长江一日游——游艇租赁

算法设计:

算法图解:







伪代码:

void rent()
{
int i,j,k,d;
for(d=3;d<=n;d++) //将问题分为小规模d
{
for(i=1;i<=n-d+1;i++)
{
j=i+d-1;
for(k=i+1;k<j;k++) //记录每一个小规模内的最优解
{
int temp;
temp=m[i][k]+m[k][j];
if(temp<m[i][j])
{
m[i][j]=temp;
s[i][j]=k;
}
}
}
}
} 
void print(int i,int j)
{
if(s[i][j]==0 )
{
cout << "--"<<j;
return ;
}
print(i,s[i][j]);
print(s[i][j],j);
}完整代码:
//program 4-3
#include<iostream>
using namespace std;
const int ms = 1000;
int r[ms][ms],m[ms][ms],s[ms][ms]; //i到j站的租金
int n; //共有n个站点
void rent()
{
int i,j,k,d;
for(d=3;d<=n;d++) //将问题分为小规模为d
{
for(i=1;i<=n-d+1;i++)
{
j=i+d-1;
for(k=i+1;k<j;k++) //记录每一个小规模内的最优解
{
int temp;
temp=m[i][k]+m[k][j];
if(temp<m[i][j])
{
m[i][j]=temp;
s[i][j]=k;
}
}
}
}
}
void print(int i,int j)
{
if(s[i][j]==0 )
{
cout << "--"<<j;
return ;
}
print(i,s[i][j]);
print(s[i][j],j);
}
int main()
{
int i,j;
cout << "请输入站点的个数 n:";
cin >> n;
cout << "请依次输入各站点之间的租金:";
for(i=1;i<=n;i++)
for(j=i+1;j<=n;++j)
{
cin>>r[i][j];
m[i][j]=r[i][j];
}
rent();
cout << "花费的最少租金为:" <<m[1][n] << endl;
cout <<"最少租金经过的站点:"<<1;
print(1,n);
return 0;
}输入输出:

例题5:快速计算——矩阵连乘

算法设计:

图解算法:




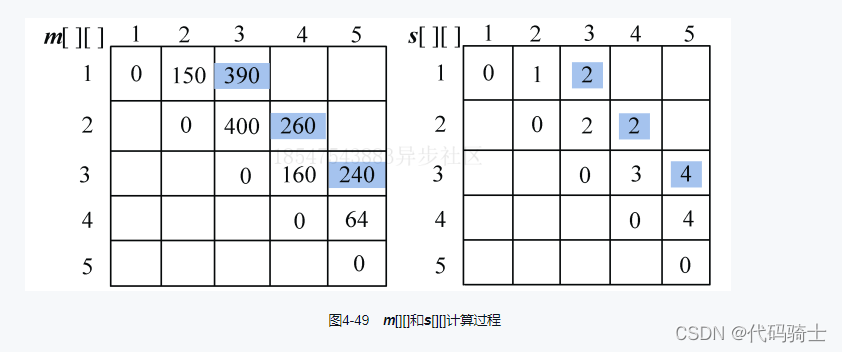


 伪代码:
伪代码:


void print(int i,int j)
{
if( i == j )
{
cout <<"A[" << i << "]";
return ;
}
cout << "(";
print(i,s[i][j]);
print(s[i][j]+1,j);
cout << ")";
}完整代码:
//program 4-4
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int msize = 100;
int p[msize];
int m[msize][msize],s[msize][msize];
int n;
void matrixchain()
{
int i,j,r,k;
memset(m,0,sizeof(m));
memset(s,0,sizeof(s));
for(r = 2; r <= n; r++) //不同规模的子问题
{
for(i = 1; i <= n-r+1; i++)
{
j = i + r - 1;
m[i][j] = m[i+1][j] + p[i-1] * p[i] * p[j]; //决策为k=i的乘法次数
s[i][j] = i; //子问题的最优策略是i;
for(k = i+1; k < j; k++) //对从i到j的所有决策,求最优值,记录最优策略
{
int t = m[i][k] + m[k+1][j] + p[i-1] * p[k] * p[j];
if(t < m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
void print(int i,int j)
{
if( i == j )
{
cout <<"A[" << i << "]";
return ;
}
cout << "(";
print(i,s[i][j]);
print(s[i][j]+1,j);
cout << ")";
}
int main()
{
cout << "请输入矩阵的个数 n:";
cin >> n;
int i ,j;
cout << "请依次输入每个矩阵的行数和最后一个矩阵的列数:";
for (i = 0; i <= n; i++ )
cin >> p[i];
matrixchain();
print(1,n);
cout << endl;
cout << "最小计算量的值为:" << m[1][n] << endl;
}输入输出:

例题6:切呀切披萨——最优三角剖分

例题7:小石子游戏——石子合并

例题8:大卖场购物车——0-1背包问题

算法设计:

图解算法:







伪代码:

for(i=1;i<= n;i++) //计算c[i][j]
for(j=1;j<=W;j++)
if(j<w[i]) //当物品的重量大于购物车的容量,则不放此物品
c[i][j] = c[i-1][j];
else //否则比较此物品放与不放是否能使得购物车内的价值最大
c[i][j] = max(c[i-1][j],c[i-1][j-w[i]] + v[i]);
cout<<"装入购物车的最大价值为:"<<c[n][W]<<endl;

//逆向构造最优解
j=W;
for(i=n;i>0;i--)
if(c[i][j]>c[i-1][j])
{
x[i]=1;
j-=w[i];
}
else
x[i]=0;
cout<<"装入购物车的物品为:";
for(i=1;i<=n;i++)
if(x[i]==1)
cout<<i<<" ";完整代码:
//program 4-7
#include <iostream>
#include<cstring>
using namespace std;
#define maxn 10005
#define M 105
int c[M][maxn]; //c[i][j] 表示前i个物品放入容量为j购物车获得的最大价值
int w[M],v[M]; //w[i] 表示第i个物品的重量,v[i] 表示第i个物品的价值
int x[M]; //x[i]表示第i个物品是否放入购物车
int main(){
int i,j,n,W; //n表示n个物品,W表示购物车的容量
cout << "请输入物品的个数n:";
cin >> n;
cout << "请输入购物车的容量W:";
cin >> W;
cout << "请依次输入每个物品的重量w和价值v,用空格分开:";
for(i=1;i<=n;i++)
cin>>w[i]>>v[i];
for(i=0;i<=n;i++) //初始化第0列为0
c[i][0]=0;
for(j=0;j<=W;j++) //初始化第0行为0
c[0][j]=0;
for(i=1;i<= n;i++) //计算c[i][j]
for(j=1;j<=W;j++)
if(j<w[i]) //当物品的重量大于购物车的容量,则不放此物品
c[i][j] = c[i-1][j];
else //否则比较此物品放与不放是否能使得购物车内的价值最大
c[i][j] = max(c[i-1][j],c[i-1][j-w[i]] + v[i]);
cout<<"装入购物车的最大价值为:"<<c[n][W]<<endl;
//逆向构造最优解
j=W;
for(i=n;i>0;i--)
if(c[i][j]>c[i-1][j])
{
x[i]=1;
j-=w[i];
}
else
x[i]=0;
cout<<"装入购物车的物品为:";
for(i=1;i<=n;i++)
if(x[i]==1)
cout<<i<<" ";
return 0;
}输入输出:

例题9:快速定位——最优二叉搜索