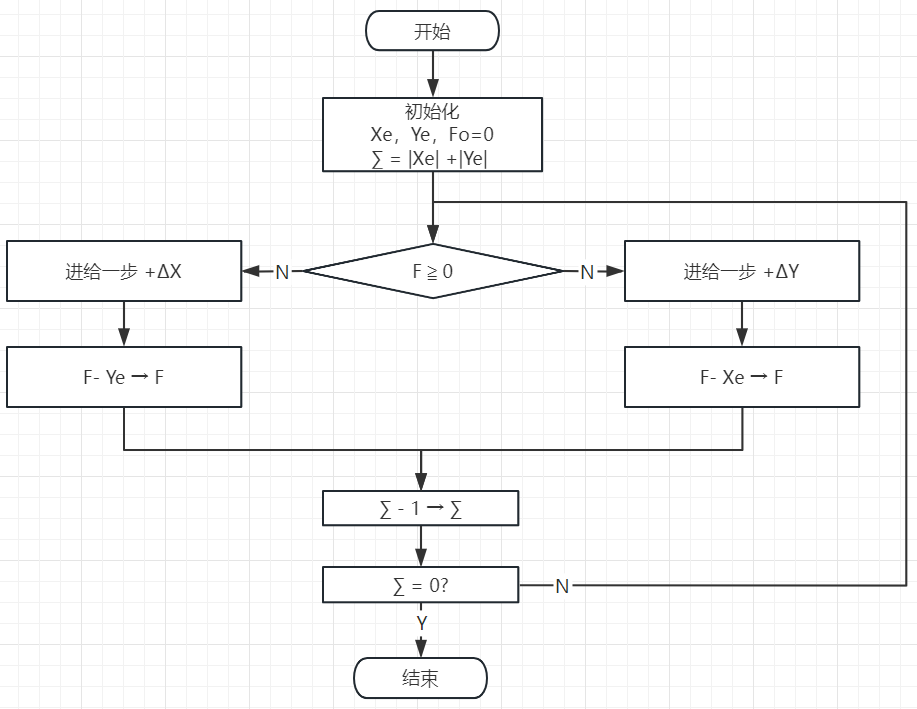
逐点比较法直线插补流程

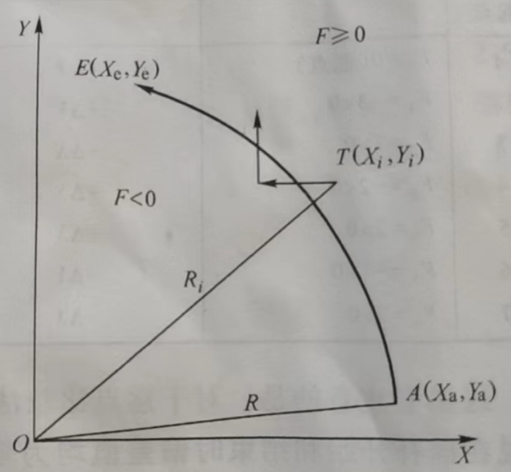
逐点比较法第I象限逆圆插补 在圆弧加工过程中，要描述刀具位置与被加工圆弧之间的相对位置关系，可用动点到圆心的距离大小来反映。

如下图所示，假设被加工零件的轮廓为第I象限逆圆弧AE，刀具位于点T(X，Y)处，圆心为0(0，0)，半径为 R，则通过比较点T到圆心的距离与圆弧半径R的大小就可以判断出刀具与圆弧之间的相对位置关系。

当点T(X，Y)正好落在圆弧AB上时，则有下式成立

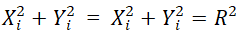
当点T落在圆弧AE外侧时，则有下式成立

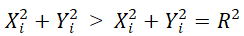
当点T落在圆弧AE内侧时，则有下式成立

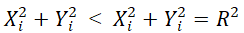
所以，取圆弧插补时的偏差函数表达式为

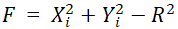
若F≥0，刀具沿-X轴方向进给一步，到达新的位置，新的偏差函数为

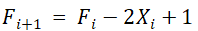
同理，若 F<0，刀具沿+Y轴方向进给一步，到达新的位置，新的偏差函数为

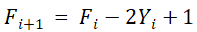
和直线插补一样，插补过程中也要进行终点判别。总的步长为

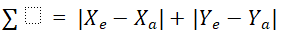
不同象限圆弧的步进给进如下图所示，据此可以得出给进脉冲分配图。

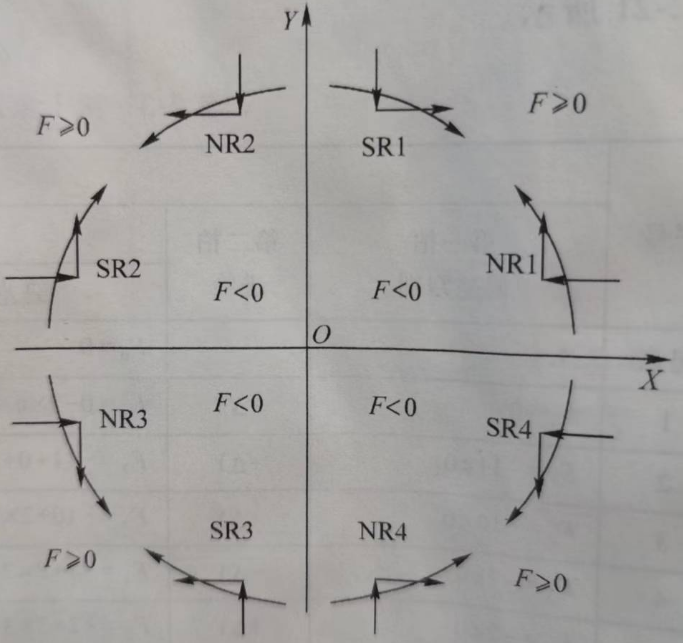
例子

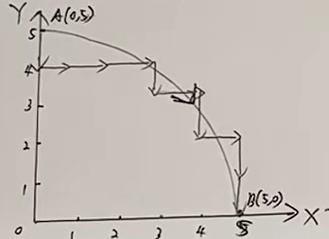
现欲加工第I象限逆圆弧AB，如图所示，起点A(0，5)，终点B (5，0)。试用逐点比较法对该段圆弧进行插补，并画出刀具运动轨迹。

总步数E步数为 |Xe-Xa|+|Ye-Ya| = 10；

步数	【第一拍】偏差判断	【第二拍】坐标给进	【第三拍】偏差计算	【第四拍】坐标计算	【第四拍】终点判别
0			F(0,0) =0	X0 = 0，Y0 = 5	E = 10
1	F(0,0) ≥0	-Y	F(1,0) = 0-2x5+1 = -9	X0 = 0，Y0 = 4	E = 9
2	F(0,1) < 0	+X	F(1,1) = -9+2x0+1= -8	X0 = 1，Y0 = 4	E = 8
3	F(1,1) <0	+X	F(2,1) = -8+2x1+1 = -5	X0 = 2，Y0 = 4	E = 7
4	F(2,1) < 0	+X	F(3,1) =-5+2x2+1= 0	X0 = 3，Y0 = 4	E = 6
5	F(3,1) ≥0	-Y	F(3,2) 0-2x4+1= -7	X0 = 3，Y0 = 3	E = 5
6	F(3,2) < 0	+X	F(4,2) = -7+2x3+1= 0	X0 = 4，Y0 = 3	E = 4
7	F(4,2) ≥ 0	-Y	F(4,3) = 0-2x3+1= -5	X0 = 4，Y0 = 2	E = 3
8	F(4,3) < 0	+X	F(5,3) = -5+2x4+1= 4	X0 = 5，Y0 = 2	E = 2
9	F(5,3) ≥ 0	-Y	F(5,4) = 4-2x2+1= 1	X0 = 5，Y0 = 1	E = 1
10	F(5,4) ≥0	-Y	F(5,5) = 1+2x1+1= 0	X0 = 5，Y0 = 5	E = 0