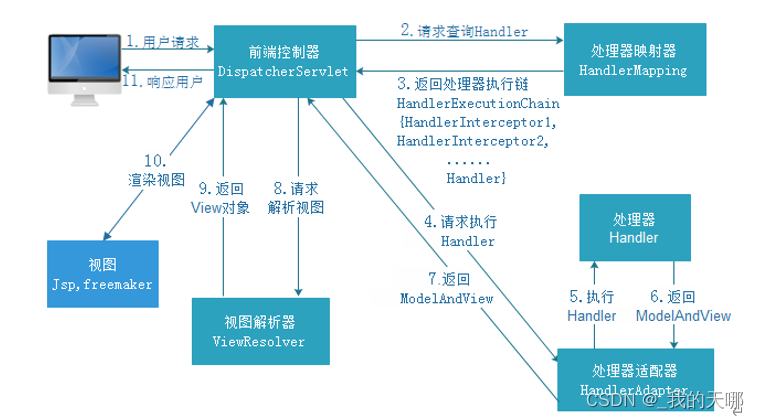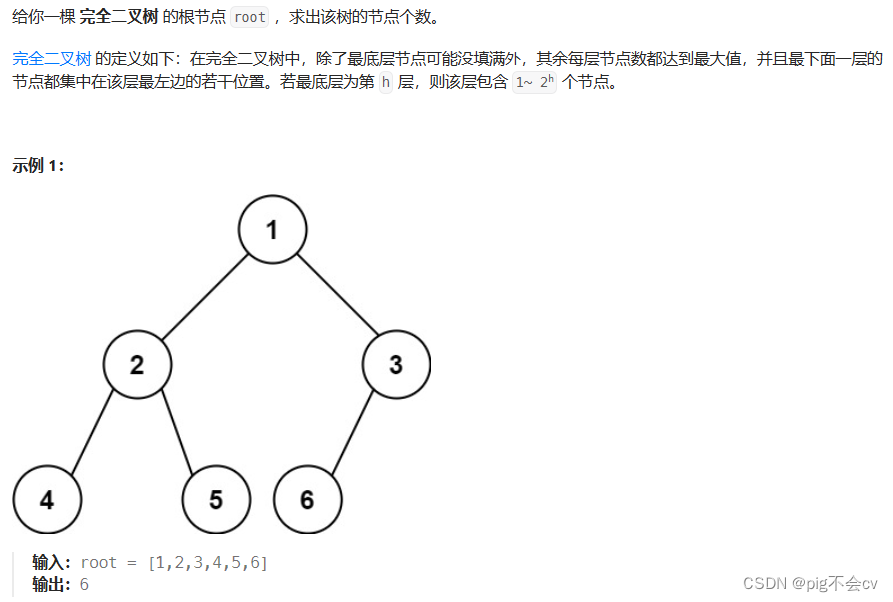
算法：

如果不考虑完全二叉树的特性，直接把完全二叉树当作普通二叉树求节点数，其实也很简单。

递归法：

用什么顺序遍历都可以。

比如后序遍历（LRV）：不断遍历左右子树的节点数，最后加上根节点的节点数1

迭代法：

用层序遍历，改一下模版代码就行。

正确代码：

递归法：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if root == None:
            return 0
        #左
        leftnum = self.countNodes(root.left)

        #右
        rightnum = self.countNodes(root.right)

        #中
        num = 1 + leftnum + rightnum

        return num

时间空间复杂度：

时间复杂度分析：

在最坏情况下，需要遍历二叉树的所有节点才能计算节点的数量。因此，时间复杂度为O(n)，其中n是二叉树中的节点数。

空间复杂度分析：

递归调用的空间复杂度取决于递归的深度，即树的高度。在最坏情况下，二叉树是一个链表结构，高度为n。因此，递归调用的空间复杂度为O(n) - 此外，除了递归调用的空间，没有使用额外的数据结构。因此，除了递归调用的空间外，空间复杂度为O(1)。

综上所述，时间复杂度为O(n)，空间复杂度为O(n)（由于递归调用的空间）或O(1)（除了递归调用的空间）。