文章目录
介绍
特征缩放
示例代码
硬间隔与软间隔分类
主要代码
代码解释
结语
介绍
作用:判别种类
原理:找出一个决策边界,判断数据所处区域来识别种类
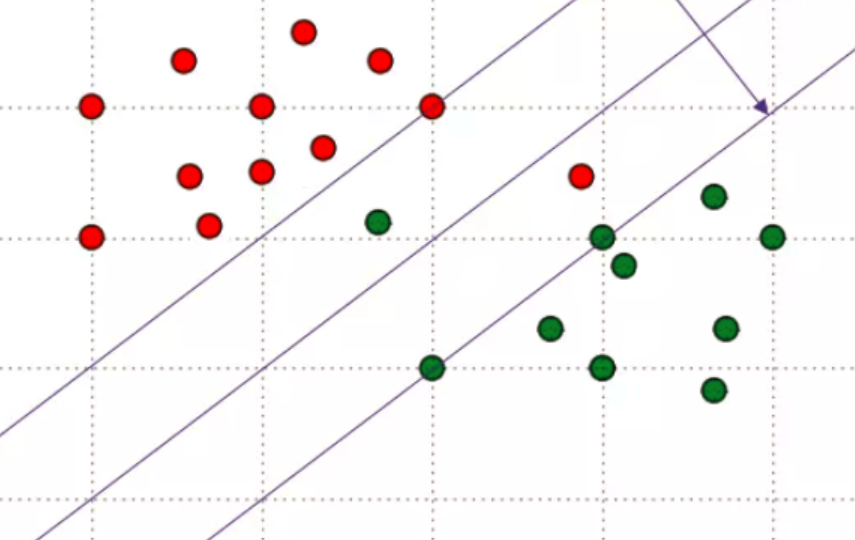
简单介绍一下SVM分类的思想,我们看下面这张图,两种分类都很不错,但是我们可以注意到第二种的决策边界与实例更远(它们之间的距离比较宽),而SVM分类就是一种寻找距每种实例最远的决策边界的算法
特征缩放
SVM算法对特征缩放很敏感(不处理算法效果会受很大影响)
特征缩放是什么意思呢,例如有身高数据和体重数据,若身高是m为单位,体重是g为单位,那么体重就比身高的数值大很多,有些机器学习算法就可能更关注某一个值,这时我们用特征缩放就可以把数据统一到相同的尺度上
示例代码
from sklearn.preprocessing import StandardScaler
import numpy as np
# 创建一个示例数据集
data = np.array([[1.0, 2.0, 3.0],
[4.0, 5.0, 6.0],
[7.0, 8.0, 9.0]])
# 创建StandardScaler对象
scaler = StandardScaler()
# 对数据进行标准化
scaled_data = scaler.fit_transform(data)
print("原始数据:\n", data)
print("\n标准化后的数据:\n", scaled_data)
# 结果是
# [[-1.22474487 -1.22474487 -1.22474487]
# [ 0. 0. 0. ]
# [ 1.22474487 1.22474487 1.22474487]]
StandardScaler是一种数据标准化的方法,它对数据进行线性变换,使得数据的均值变为0,标准差变为1。
解释上面的数据
在每列上进行标准化,即对每个特征进行独立的标准化。每个数值是通过减去该列的均值,然后除以该列的标准差得到的。
- 第一列:(1−4)/9=−1.22474487(1−4)/9=−1.22474487,(4−4)/9=0(4−4)/9=0,(7−4)/9=1.22474487(7−4)/9=1.22474487。
- 第二列:(2−5)/9=−1.22474487(2−5)/9=−1.22474487,(5−5)/9=0(5−5)/9=0,(8−5)/9=1.22474487(8−5)/9=1.22474487。
- 第三列:(3−6)/9=−1.22474487(3−6)/9=−1.22474487,(6−6)/9=0(6−6)/9=0,(9−6)/9=1.22474487(9−6)/9=1.22474487。
这样,标准化后的数据集就符合标准正态分布,每个特征的均值为0,标准差为1。
硬间隔与软间隔分类
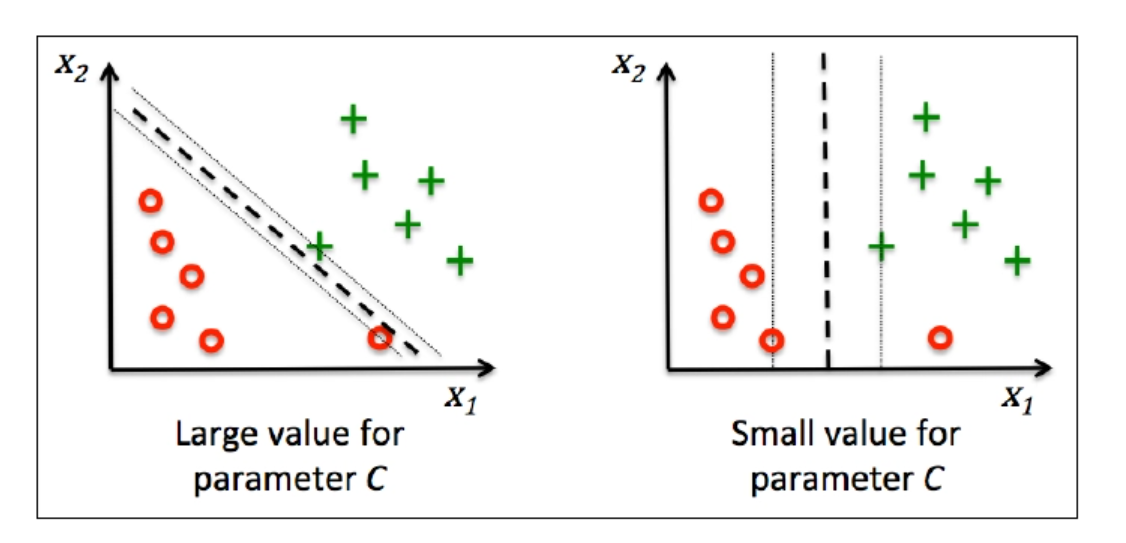
硬间隔分类就是完全将不同的个体区分在不同的区域(不能有一点误差)

软间隔分类就是允许一些偏差(图中绿和红色的点都有一些出现在了对方的分区里)
硬间隔分类往往会出现一些问题,例如有时候模型不可能完全分成两类,同时,硬间隔分类往往可能导致过拟合,而软间隔分类的泛化能力就比硬间隔分类好很多
主要代码
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
model = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge"))
])
model.fit(x, y)代码解释
在这里,Pipeline的构造函数接受一个由元组组成的列表。每个元组的第一个元素是该步骤的名称(字符串),第二个元素是该步骤的实例。在这个例子中,第一个步骤是数据标准化,使用StandardScaler,命名为"scaler";第二个步骤是线性支持向量机,使用LinearSVC,命名为"linear_svc"。这两个步骤会按照列表中的顺序依次执行。
参数C是正则程度,hinge是SVM分类算法的损失函数,用来训练模型
结语
SVM分类是一种经典的分类算法,也叫大间隔分类算法。