图源:文心一言
考研笔记整理~🥝🥝
之前的博文链接在此:数据结构02:线性表[顺序表+链表]_线性链表-CSDN博客~🥝🥝
本篇作为线性表的代码补充,每道题提供了优解和暴力解算法,供小伙伴们参考~🥝🥝
- 第1版:无情地Push Chat GPT老师写代码、分析GPT老师写的代码并思考弱智解~🧩🧩
编辑:梅头脑🌸
参考用书:王道考研《2024年 数据结构考研复习指导》
📇目录
📇目录
🧵2010统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
⌨️优解演算
🌰暴力解
📇暴力解思路
⌨️暴力解代码
⌨️暴力解演算
🧵2011统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
⌨️优解演算
🌰暴力解
📇暴力解思路
⌨️暴力解代码
⌨️暴力解演算
🧵2013统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
⌨️优解演算
🌰暴力解
📇暴力解思路
⌨️暴力解代码
⌨️暴力解演算
🧵2018统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
🧵2020统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
🌰暴力解
📇暴力解思路
⌨️暴力解代码
🔚结语
🧵2010统考真题
🧩题目
设将n个整数存放到一维数组R中。设计一个在时间和空间两方面都尽可能高效的算法。将R中保存的序列循环左移p个位置,即将R的数据由(X0,X1,…,Xn-1)变换为(Xp,Xp+1,…Xn-1,X0,X1,…,Xp-1)。
🌰优解
📇优解思路
- 算法思想:
- 将数组p(n-p)转化为数组(n-p)p,(n-p)p=(p-1(n-p)-1)-1;
- 因此分别反转前p项,后n-p项,最后整体反转p-1(n-p)-1;
- reverse函数用于反转数组中指定范围的元素,它通过交换两端的元素来实现反转。
- 时间复杂度:O(n),其中n是数组的长度,因为需要反转数组的两部分和整体数组。
- 空间复杂度:O(1),因为算法只使用了固定的额外空间来存储一些临时变量,与数组的长度无关。
⌨️优解代码
#include <iostream>
using namespace std;
// 反转数组中指定范围的元素
void reverse(int arr[], int start, int end) {
// 使用双指针法将数组中指定范围的元素进行反转
// start 指向要反转的范围的起始位置,end 指向要反转的范围的末尾位置
while (start < end) {
// 交换 start 和 end 位置的元素
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
// 向中间移动双指针
start++;
end--;
}
}
// 执行循环左移操作
void rotateLeft(int arr[], int n, int p) {
// 将左移位数取模以确保它在数组长度范围内
p = p % n;
if (p == 0) return; // 如果左移位数为0,直接返回,不需要进行操作
reverse(arr, 0, p - 1); // 反转前半部分
reverse(arr, p, n - 1); // 反转后半部分
reverse(arr, 0, n - 1); // 整体反转
}
int main() {
const int n = 10; // 数组长度为10
const int p = 3; // 左移3位
int arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; // 初始化数组元素
rotateLeft(arr, n, p); // 执行左移操作
// 输出结果
cout << "左移后的数组为: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
⌨️优解演算
- 初始轮 arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; temp = NULL;
- 第一轮 arr[n] = {2, 1, 0, 3, 4, 5, 6, 7, 8, 9}; temp = 0;
- 第二轮 arr[n] = {2, 1, 0, 9, 8, 7, 6, 5, 4, 3}; temp = 3;temp = 4;temp = 5;
- 第三轮 arr[n] = {3, 4, 5, 6, 7, 8, 9, 0, 1, 2}; temp = 2;temp = 1;temp = 0;temp = 9;temp = 8;
🌰暴力解
📇暴力解思路
- 算法思想:
- 创建一个临时数组 temp,用于存储前p个元素。
- 将后面的元素向前移动p个位置,留出前p个位置用于粘贴临时数组的内容。
- 将临时数组中的元素复制回原数组的末尾。
- 时间复杂度:O(n),因为我们额外使用了一个临时数组 temp 来存储前p个元素。这个临时数组的大小与左移的位数p相等,因此空间复杂度是O(p),而在最坏情况下,p可以等于n,所以空间复杂度可以达到O(n)。
- 空间复杂度:O(n),理由同上。
⌨️暴力解代码
#include <iostream>
using namespace std;
void rotateLeft(int arr[], int n, int p) {
int temp[p]; // 创建一个临时数组用于存储前p个元素
// 复制前p个元素到临时数组中
for (int i = 0; i < p; i++) {
temp[i] = arr[i];
}
// 将后面的元素向前移动p个位置
for (int i = p; i < n; i++) {
arr[i - p] = arr[i];
}
// 将临时数组中的元素复制回原数组末尾
for (int i = 0; i < p; i++) {
arr[n - p + i] = temp[i];
}
}
int main() {
const int n = 10; // 数组长度为10
const int p = 3; // 左移3位
int arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; // 初始化数组元素
rotateLeft(arr, n, p); // 执行左移操作
// 输出结果
cout << "左移后的数组为: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
⌨️暴力解演算
- 初始轮 arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; temp[p] = NULL;
- 第一轮 arr[n] = {2, 1, 0, 3, 4, 5, 6, 7, 8, 9}; temp[p] = {2, 1, 0};
- 第二轮 arr[n] = {3, 4, 5, 6, 7, 8, 9, 7, 8, 9}; temp[p] = {2, 1, 0};
- 第三轮 arr[n] = {3, 4, 5, 6, 7, 8, 9, 0, 1, 2}; temp[p] = {2, 1, 0};
🧵2011统考真题
🧩题目
一个长度为L的升序序列S,处在第[L/2]个位置的元素称为S的中位数。例如,若序列S1=(11,13,15,17,19),则S1的中位数是15,两个序列的中位数是他们所有元素的升序序列的中位数。例如若S2=(2,4,6,8,10),则S1和S2的中位数是11。现在有两个等长的升序序列A和B,试设计在一个时间和空间两方面都尽可能高效的算法,找出两个序列A和B的中位数。
🌰优解
📇优解思路
- 算法思想:
- 检查A和B的中间位置的元素,分别记为a_mid和b_mid。
如果a_mid等于b_mid,那么它们就是两个序列的中位数,直接返回a_mid或b_mid都可以。
如果a_mid小于b_mid,说明A的中位数位于A的后半部分和B的前半部分之间,将A的前半部分和B的后半部分丢弃,继续在剩下的部分中查找中位数。
如果a_mid大于b_mid,说明B的中位数位于B的后半部分和A的前半部分之间,将B的前半部分和A的后半部分丢弃,继续在剩下的部分中查找中位数。
- 重复上述步骤,直到找到中位数。
- 时间复杂度:O(log(min(La, Lb))),其中La和Lb分别是序列A和B的长度。这是因为在每一步中,我们都将输入规模减少一半。
- 空间复杂度:O(1),因为它只使用了一些变量来存储中间结果,而不需要额外的数据结构。
- 备注:这段程序好像不能在网上的在线编译器跑,会显示“‘INT_MIN’ was not declared in this scope”。
⌨️优解代码
#include <iostream>
using namespace std;
// 函数:findMedianSortedArrays
// 参数:两个升序数组A和B,以及它们的长度La和Lb
// 返回值:两个数组的中位数
double findMedianSortedArrays(int A[], int B[], int La, int Lb) {
// 确保La小于等于Lb,方便后续处理
if (La > Lb) {
swap(A, B);
swap(La, Lb);
}
// 初始化左边界和右边界,以及两数组的中位数的位置(结果向下取整)
int left = 0, right = La;
int halfLen = (La + Lb + 1) / 2;
// 使用二分查找在数组A中找到合适的位置
while (left < right) {
int i = left + (right - left) / 2;
int j = halfLen - i;
int round = 1;
// cout << "Round " << round++ << ":" << endl;
// cout << "i = " << i << ", j = " << j << endl;
// 通过比较A[i]和B[j-1]来调整i的位置
if (A[i] < B[j - 1])
left = i + 1;
else
right = i;
// cout << "After comparison, left = " << left << ", right = " << right << endl << endl;
}
// 计算中位数所在的位置
int i = left, j = halfLen - left;
// 计算四个关键值,用于求解中位数
int AleftMax = (i == 0) ? INT_MIN : A[i - 1]; //如果i等于0(也就是A的左边界),那么将AleftMax设为整型的最小值 INT_MIN(通常是-2147483648)。否则,将AleftMax设为A中下标为i-1的元素的值。
int ArightMin = (i == La) ? INT_MAX : A[i];
int BleftMax = (j == 0) ? INT_MIN : B[j - 1];
int BrightMin = (j == Lb) ? INT_MAX : B[j];
// cout << "Final values:" << endl;
// cout << "i = " << i << ", j = " << j << endl;
// cout << "AleftMax = " << AleftMax << ", ArightMin = " << ArightMin << endl;
// cout << "BleftMax = " << BleftMax << ", BrightMin = " << BrightMin << endl;
// 根据数组总长度的奇偶性返回中位数
if ((La + Lb) % 2 == 1)
return max(AleftMax, BleftMax);
else
return (max(AleftMax, BleftMax) + min(ArightMin, BrightMin)) / 2.0;
}
int main() {
int A[] = {11, 13, 15, 17, 19}; // 第一个升序数组
int B[] = {2, 4, 6, 8, 20}; // 第二个升序数组
int La = sizeof(A) / sizeof(A[0]); // 第一个数组的长度,将数组占用内存的总字节数除以第一个元素占用的字节数,我们得到了数组中元素的个数,也就是数组的长度。
int Lb = sizeof(B) / sizeof(B[0]); // 第二个数组的长度
double median = findMedianSortedArrays(A, B, La, Lb); // 调用函数计算中位数
cout << "中位数是: " << median << endl; // 输出中位数
return 0;
}
⌨️优解演算
初始:
int A[] = {11, 13, 15, 17, 19};
int B[] = {2, 4, 6, 8, 20};
int La = 5;
int Lb = 5;
halfLen = (La + Lb + 1) / 2 = (5 + 5 + 1) / 2 = 11 / 2 = 5;
left = 0;
right = La = 5;第一轮循环:
i = 0 + ( 5 - 0 ) / 2 = 2, j = 5 - 2 = 3;
A[i = 2] = 15, B[j - 1 = 2] = 6;
A[i] 大于 B[j - 1],所以更新 right = i = 2第二轮循环:
i = 0 + ( 2 - 0 ) / 2 = 1, j = 5 - 1 = 4;
A[i = 1] = 13, B[4 - 1 = 3] = 8;
A[i] 大于 B[j - 1],所以更新 right = i = 1第三轮循环:
i = 0 + ( 1 - 0 ) / 2 = 0, j = 5 - 0 = 5;
A[i = 0] = 11, B[5 - 1 = 4] = 20;
A[i] 小于 B[j - 1],所以更新 left = j = 1不满足while循环条件,跳出:
i = j = 1; j = 5-1 = 4;
AleftMax = A[i-1] = 11, ArightMin = A[1] = 13;
BleftMax = B[j-1] = 8, BrightMin = B[j] = 20;(La + Lb) % 2 = (5 + 5) % 2 = 10 % 2 = 0;
max(AleftMax, BleftMax) + min(ArightMin, BrightMin)) / 2.0 = max(11+13)/2 =12
🌰暴力解
📇暴力解思路
- 算法思想:将两个数组合并后排序,然后找到合并后数组的中位数;
- 时间复杂度:O(La + Lb);
- 空间复杂度:O(La + Lb);
⌨️暴力解代码
#include <iostream>
#include <vector>
using namespace std;
double findMedianSortedArrays(int A[], int B[], int La, int Lb) {
// 将数组A和数组B合并到一个新的数组C中
vector<int> C;
int i = 0, j = 0;
while (i < La && j < Lb) {
if (A[i] <= B[j]) {
C.push_back(A[i]);
i++;
} else {
C.push_back(B[j]);
j++;
}
}
while (i < La) {
C.push_back(A[i]);
i++;
}
while (j < Lb) {
C.push_back(B[j]);
j++;
}
// 计算合并后数组C的长度
int Lc = C.size();
// 计算中位数的位置
int mid = Lc / 2;
if (Lc % 2 == 1) {
return C[mid];
} else {
return (C[mid - 1] + C[mid]) / 2.0;
}
}
int main() {
int A[] = {11, 13, 15, 17, 19};
int B[] = {2, 4, 6, 8, 20};
int La = sizeof(A) / sizeof(A[0]);
int Lb = sizeof(B) / sizeof(B[0]);
double median = findMedianSortedArrays(A, B, La, Lb);
cout << "中位数是: " << median << endl;
return 0;
}⌨️暴力解演算
- int A[] = {11, 13, 15, 17, 19}; int B[] = {2, 4, 6, 8, 20};
- vector<int> C = {2, 4, 6, 8, 11, 13, 15, 17, 19};
Lc = (C[4 ]+ C[5])/2 = 12;
🧵2013统考真题
🧩题目
已知一个整数序列A=(a0,a1,…,an),其中0≤ai≤n。若存在ap1=ap2=…=apm=x 且 m > n/2 (0≤pk<n,1≤k≤m),则称x为A的主元素。例如A=(0,5,5,3,5,7,5,5),则5为主元素;又如A=(0,5,5,3,5,1,5,7),则A中没有主元素。假设A中的n个元素保存在一个一维数组中,请设计一个尽可能高效的算法,找出A的主元素。若存在主元素,则输出该元素;否则输出-1。
🌰优解
📇优解思路
- 算法思想:"摩尔投票算法"
- 遍历数组并维护一个候选主元素以及一个计数器;
- 在遍历过程中,如果计数器为零,就将当前元素设为候选主元素;否则,如果当前元素与候选主元素相同,计数器增加,否则计数器减少。最后剩下的候选主元素可能就是主元素;
- 但还需要再次遍历数组确认它是否真的满足主元素的条件。
- 时间复杂度:O(n),其中n是输入数组的长度。算法需要进行两次遍历,每次遍历的时间复杂度都是O(n)。
- 空间复杂度:O(1),因为它只使用了常数级别的额外空间来存储候选主元素和计数器,而不随输入规模变化。
⌨️优解代码
#include <iostream>
using namespace std;
int findMajorityElement(int A[], int n) {
int candidate = -1;
int count = 0;
// 第一轮遍历,选出候选主元素
for (int i = 0; i < n; i++) {
// cout << "candidate = A[" << i << "] = " << candidate << ", count = " << count << endl;
if (count == 0) {
candidate = A[i];
count = 1;
} else {
if (A[i] == candidate) {
count++;
} else {
count--;
}
}
}
// 第二轮遍历,确认候选主元素是否真的是主元素
count = 0;
for (int i = 0; i < n; i++) {
if (A[i] == candidate) {
count++;
}
}
// cout << "count = " << count << endl;
if (count > n / 2) {
return candidate;
} else {
return -1;
}
}
int main() {
int A[] = {0, 5, 5, 3, 5, 7, 5, 5};
int B[] = {0, 5, 5, 3, 5, 1, 5, 7};
int La = sizeof(A) / sizeof(A[0]);
int Lb = sizeof(B) / sizeof(B[0]);
int resultA = findMajorityElement(A, La);
int resultB = findMajorityElement(B, Lb);
if (resultA != -1) {
cout << "数组A的主元素是:" << resultA << endl;
} else {
cout << "数组A没有主元素" << endl;
}
if (resultB != -1) {
cout << "数组B的主元素是:" << resultB << endl;
} else {
cout << "数组B没有主元素" << endl;
}
return 0;
}
⌨️优解演算
数组A
candidate = A[0] = -1, count = 0
candidate = A[1] = 0, count = 1
candidate = A[2] = 0, count = 0
candidate = A[3] = 5, count = 1
candidate = A[4] = 5, count = 0
candidate = A[5] = 5, count = 1
candidate = A[6] = 5, count = 0
candidate = A[7] = 5, count = 1
count = 5,count > 8/2数组B
candidate = A[0] = -1, count = 0
candidate = A[1] = 0, count = 1
candidate = A[2] = 0, count = 0
candidate = A[3] = 5, count = 1
candidate = A[4] = 5, count = 0
candidate = A[5] = 5, count = 1
candidate = A[6] = 5, count = 0
candidate = A[7] = 5, count = 1
count = 4,count ≤ 8/2
🌰暴力解
📇暴力解思路
- 算法思想:
- 统计每种元素的出现次数,然后找到出现次数最多的元素。
- 第一遍遍历数组,统计每种元素的出现次数,可以使用一个哈希表或者数组来存储。
- 第二遍遍历统计结果,找到出现次数最多的元素。
- 检查该元素的出现次数是否大于总长度除以2,如果满足条件,则它是主元素,否则不存在主元素。
- 时间复杂度:O(n),其中n是输入数组的长度。
- 空间复杂度:O(n),取决于不同元素的数量,最坏情况下可能会达到O(n)。
⌨️暴力解代码
#include <iostream>
#include <unordered_map>
using namespace std;
int findMajorityElement(int A[], int n) {
// 使用哈希表 counter 统计每个元素的出现次数
unordered_map<int, int> counter;
// 第一次遍历,统计每个元素的出现次数
for (int i = 0; i < n; i++) {
counter[A[i]]++;
}
// 测试:输出哈希表的值
// cout << "Counter:" << endl;
// for (auto& pair : counter) {
// cout << pair.first << ": " << pair.second << endl;
// }
// 找到出现次数最多的元素
int maxCount = 0;
int majorityElement = -1;
for (auto& pair : counter) { // 声明一个名为 pair 的变量,它的类型会根据 counter 中的元素类型自动推断(因为我们使用了 auto)。pair 实际上是一个键值对,包括一个键(pair.first)和一个值(pair.second)。
// 测试:输出所有参数的值
// cout << "pair.first = " << pair.first << ", pair.second = " << pair.second << endl;
// cout << "maxCount = " << maxCount << ", majorityElement = " << majorityElement << endl;
if (pair.second > maxCount) { // 比较当前键值对的值(也就是元素出现的次数 pair.second)和 maxCount 的大小
maxCount = pair.second; // 如果当前元素出现的次数大于 maxCount,则更新 maxCount 和 majorityElement
majorityElement = pair.first; // 将当前元素作为候选主元素
}
}
// 检查出现次数是否大于总长度的一半
if (maxCount > n / 2) {
return majorityElement;
} else {
return -1;
}
}
int main() {
int A[] = {0, 5, 5, 3, 5, 7, 5, 5};
int B[] = {0, 5, 5, 3, 5, 1, 5, 7};
int La = sizeof(A) / sizeof(A[0]);
int Lb = sizeof(B) / sizeof(B[0]);
int resultA = findMajorityElement(A, La);
int resultB = findMajorityElement(B, Lb);
if (resultA != -1) {
cout << "数组A的主元素是:" << resultA << endl;
} else {
cout << "数组A没有主元素" << endl;
}
if (resultB != -1) {
cout << "数组B的主元素是:" << resultB << endl;
} else {
cout << "数组B没有主元素" << endl;
}
return 0;
}⌨️暴力解演算
- 数组A模拟:
Counter:
3: 1
7: 1
0: 1
5: 5
pair.first = 3, pair.second = 1
maxCount = 0, majorityElement = -1
pair.first = 7, pair.second = 1
maxCount = 1, majorityElement = 3
pair.first = 0, pair.second = 1
maxCount = 1, majorityElement = 3
pair.first = 5, pair.second = 5
maxCount = 1, majorityElement = 3
数组A的主元素是:5
- 数组B模拟:
Counter:
1: 1
3: 1
7: 1
0: 1
5: 4
pair.first = 1, pair.second = 1
maxCount = 0, majorityElement = -1
pair.first = 3, pair.second = 1
maxCount = 1, majorityElement = 1
pair.first = 7, pair.second = 1
maxCount = 1, majorityElement = 1
pair.first = 0, pair.second = 1
maxCount = 1, majorityElement = 1
pair.first = 5, pair.second = 4
maxCount = 1, majorityElement = 1
数组B没有主元素
🧵2018统考真题
🧩题目
给定一个含n个整数的数组,请设计一个在时间上尽可能高效的算法,找出数组中未出现的最小正整数。例如,数组{-5,3,2,3}中未出现的最小正整数是1,数组{1,2,3}中未出现的最小正整数是4。
🌰优解
📇优解思路
- 算法思想:"哈希表标记"
- 利用数组本身来进行标记,将数组元素放置到其对应的位置上;
- 然后再遍历一次数组找出第一个不符合规则的位置,即未出现的最小正整数。
- 时间复杂度:O(n),因为最多需要遍历两次数组。
- 空间复杂度:O(n),使用了一个大小与输入数组相同的数组进行操作,因此空间复杂度是线性的,与输入数组的大小成正比。
- 备注:这个算法思想应该还是挺容易想到的,因此没有暴力解。
⌨️优解代码
#include <iostream>
#include <vector>
using namespace std;
int firstMissingPositive(vector<int>& nums) {
int n = nums.size();
// 将数组元素放置到其对应的位置上
for (int i = 0; i < n; ++i) {
while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
swap(nums[i], nums[nums[i] - 1]);
}
}
// 再次遍历数组,找出第一个不符合规则的位置
for (int i = 0; i < n; ++i) {
if (nums[i] != i + 1) {
return i + 1;
}
}
return n + 1; // 如果数组本身符合规则,则返回数组长度加1
}
int main() {
vector<int> arr1 = {-5, 3, 2, 3};
vector<int> arr2 = {1, 2, 3};
int missing1 = firstMissingPositive(arr1);
int missing2 = firstMissingPositive(arr2);
cout << "数组{-5, 3, 2, 3}中未出现的最小正整数是:" << missing1 << endl;
cout << "数组{1, 2, 3}中未出现的最小正整数是:" << missing2 << endl;
return 0;
}
🧵2020统考真题
🧩题目
定义三元组(a,b,c)(a,b,c均为整数)的距离D=|a-b| + |b-c| + |c-a|。给定3个非空整数集合S1、S2和S3,按升序分别存储在3个数组中。请设计一个尽可能高效的算法,计算并输出所有可能得三元组(a,b,c)(a∈S1,b∈S2,c∈S3)中的最小距离、例如S1={-1,0,9},S2={-25,-10,-10,11},S3={2,9,17,30,41},则最小距离为2,相应的三元组为(9,10,9)。
🌰优解
📇优解思路
- 通用思路:在求解距离的问题中,通常的做法是通过遍历或者适当的比较来不断更新最小值。这种方法通常会在处理多个元素之间的关系时有效,尤其是在找到最小值或最大值时。
- 算法思想:
- 选择S1、S2和S3中的一个数作为其中一个元素(比如选择S1中的元素作为a);
- 然后在S2和S3中使用两个指针分别找到与a最接近的b和c,从而计算距离,并维护最小距离;
- 时间复杂度:O(n),emm...如果忽略那段蠢萌的vector输出的话;
- 空间复杂度:O(1),除了用于存储输入数组外,算法中没有使用额外的辅助空间。
⌨️优解代码
#include <iostream>
#include <vector>
#include <climits> // 在本示例中,INT_MAX 和 INT_MIN 分别用于初始化最小距离变量为最大可能值,以便在计算距离时进行比较,并找到最小值。
using namespace std;
int minDistanceTriplet(vector<int>& S1, vector<int>& S2, vector<int>& S3) {
int minDistance = INT_MAX;
int i = 0, j = 0, k = 0;
int size1 = S1.size(), size2 = S2.size(), size3 = S3.size();
while (i < size1 && j < size2 && k < size3) {
int a = S1[i], b = S2[j], c = S3[k];
int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);
minDistance = min(minDistance, currentDistance);
// 找到与当前 a 最接近的 b
if (a <= b && a <= c) {
i++;
} else if (b <= a && b <= c) {
j++;
} else {
k++;
}
}
return minDistance;
}
void printTriplet(int a, int b, int c) {
cout << "三元组为: (" << a << ", " << b << ", " << c << ")" << endl;
}
int main() {
vector<int> S1 = {-1, 0, 9};
vector<int> S2 = {-25, -10, 10, 11};
vector<int> S3 = {2, 9, 17, 30, 41};
int minDist = minDistanceTriplet(S1, S2, S3);
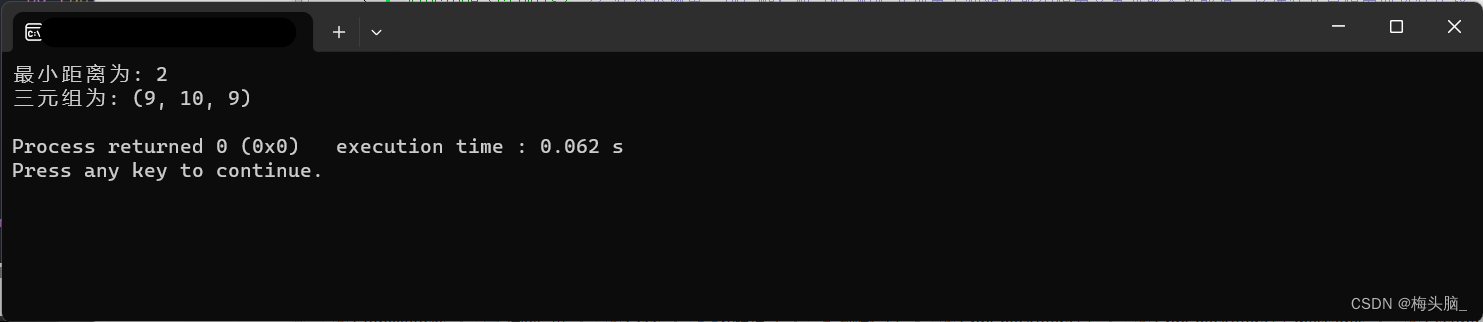
cout << "最小距离为: " << minDist << endl;
// 输出三元组
// 遍历三元组的索引,根据索引取得对应元素输出
for (int i = 0; i < S1.size(); ++i) {
for (int j = 0; j < S2.size(); ++j) {
for (int k = 0; k < S3.size(); ++k) {
int a = S1[i], b = S2[j], c = S3[k];
int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);
if (currentDistance == minDist) {
printTriplet(a, b, c);
}
}
}
}
return 0;
}
🌰暴力解
📇暴力解思路
- 算法思想:
- 使用三重循环来遍历所有可能的三元组;
- 计算每个三元组的距离并更新最小值;
- 时间复杂度:O(n),其中n是输入数组的长度;
- 空间复杂度:O(1)。
⌨️暴力解代码
#include <iostream>
#include <vector>
#include <climits> // 在本示例中,INT_MAX 和 INT_MIN 分别用于初始化最小距离变量为最大可能值,以便在计算距离时进行比较,并找到最小值。
using namespace std;
int minDistanceTriplet(vector<int>& S1, vector<int>& S2, vector<int>& S3) {
int minDistance = INT_MAX;
for (int i = 0; i < S1.size(); ++i) {
for (int j = 0; j < S2.size(); ++j) {
for (int k = 0; k < S3.size(); ++k) {
int a = S1[i], b = S2[j], c = S3[k];
int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);
minDistance = min(minDistance, currentDistance);
}
}
}
return minDistance;
}
void printTriplet(int a, int b, int c) {
cout << "三元组为: (" << a << ", " << b << ", " << c << ")" << endl;
}
int main() {
vector<int> S1 = {-1, 0, 9};
vector<int> S2 = {-25, -10, 10, 11};
vector<int> S3 = {2, 9, 17, 30, 41};
int minDist = minDistanceTriplet(S1, S2, S3);
cout << "最小距离为: " << minDist << endl;
// 输出三元组
// 遍历三元组的索引,根据索引取得对应元素输出
for (int i = 0; i < S1.size(); ++i) {
for (int j = 0; j < S2.size(); ++j) {
for (int k = 0; k < S3.size(); ++k) {
int a = S1[i], b = S2[j], c = S3[k];
int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);
if (currentDistance == minDist) {
printTriplet(a, b, c);
}
}
}
}
return 0;
}🔚结语
博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容{例如有错误、难理解、不简洁、缺功能}等,博主会顶锅前来修改~😶🌫️
我是梅头脑,本片博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下,收到点赞的话,博主肝文的动力++~🌟🌟
数据结构_梅头脑_的博客-CSDN博客![]() https://blog.csdn.net/weixin_42789937/category_12262100.html?spm=1001.2014.3001.5482
https://blog.csdn.net/weixin_42789937/category_12262100.html?spm=1001.2014.3001.5482