一、下载JDK
1.官网下载
官网地址:Java Downloads | Oracle

 大多数人的Linux操作系统都是64位的,因此我们就选择64位的压缩包文件,jdk1.8_381是jdk1.8的最新版本。
大多数人的Linux操作系统都是64位的,因此我们就选择64位的压缩包文件,jdk1.8_381是jdk1.8的最新版本。
2.百度网盘下载
链接:https://pan.baidu.com/s/1we_52oylG-elKoBsvG0YUw
提取码:4w5g
二、安装前准备工作
1.检查是否安装了OpenJDK
java -version
若安装了则会输出OpenJDK的相关版本信息
2. 采用rpm命令查看是否存在jdk
rpm -qa | grep jdk
用于在 Linux 系统上列出已安装的与 JDK(Java Development Kit)相关的 RPM 软件包。若有则采用rpm命令先删除相关jdk的软件包。
3.删除相关jdk的软件包
rpm -e --nodeps 查出来的全名称
依次删除,删除完成之后。
再使用 java -version 命令检查是否存在JDK。
三、安装JDK1.8
1.将下载好的JDK上传到服务器
![]()
2.解压JDK1.8.0_381

3.将JDK移动到/usr/local目录下,方便管理
mv jdk1.8.0_381 /usr/local/4.配置JDK环境变量
linux下/etc/profile文件是有关Linux环境变量。所以,我们要将jdk配置到/etc/profile,才可以在任何一个目录访问jdk。
vim /etc/profile在文件末尾添加
export JAVA_HOME=/usr/local/jdk1.8.0_381 #jdk安装目录
export JRE_HOME=${JAVA_HOME}/jre
export CLASSPATH=.:${JAVA_HOME}/lib:${JRE_HOME}/lib:$CLASSPATH
export JAVA_PATH=${JAVA_HOME}/bin:${JRE_HOME}/bin
export PATH=$PATH:${JAVA_PATH}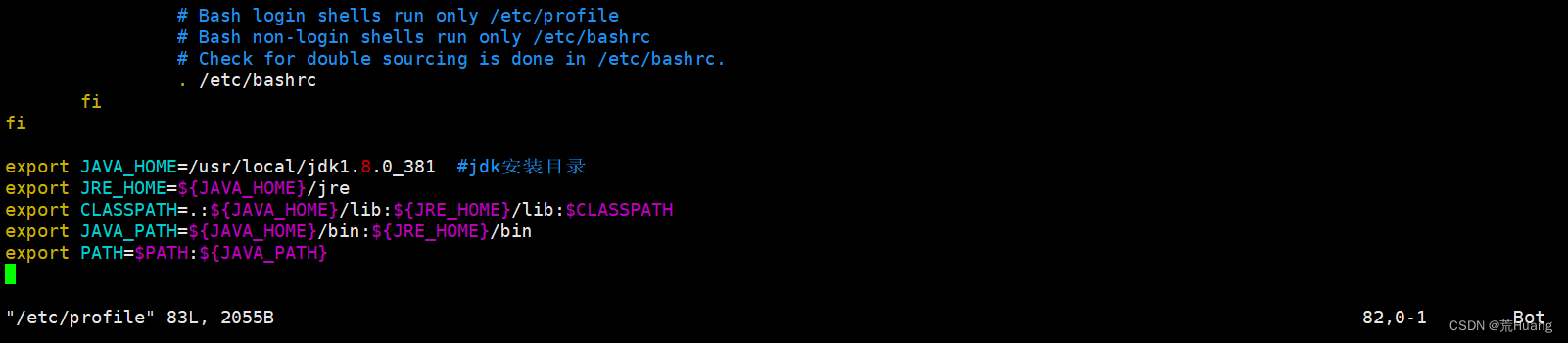
添加好了之后,保存并退出。
5.刷新配置文件
source /etc/profile四、验证java环境
1.输入 java -version和javac -version

输入上述命令后能够看到相应的版本信息而不是错误提示,那么说明您已经成功配置好了 Java 开发环境,并且可以在 Linux 中使用 java 和 javac 命令了。