文章目录
- 摘花生
- 最低通行费
- 方格取数
- 传纸条
一、摘花生OJ链接
本题思路:本题是dp问题中比较简单的模型,dp问题考虑方式:状态表示:集合:定义f[i][j]为从(1, 1)到达(i, j)的所有方案,属性:最大值。状态转移:(i, j)从(i-1, j)即上方过来,(i, j)从(i, j-1)即左方过来。当然这一题也可以进行空间压缩的方式求解。f[i][j]只需要用到这一层和上一层的f元素,所以可以压缩成滚动数组。在此之上,还可以直接压缩成一维数组。
#include <bits/stdc++.h>
constexpr int N=110;
int r,c;
int g[N][N];
int f[N][N];//表示所有从(1,1)走到(i,j)的路线的集合,该集合的属性为最大值
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--){
std::cin>>r>>c;
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
std::cin>>g[i][j];
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)//状态计算分为两种第一种是最后一步是从上面来的,第二种是从左边过来的。
f[i][j]=std::max(f[i-1][j],f[i][j-1])+g[i][j];
std::cout<<f[r][c]<<std::endl;
}
return 0;
}二、最低通行费OJ链接
本题思路:本题与上题一样的思路,要在2*N-1的时间内走完说明不能往回走。然后只需要注意边界条件即可。
#include <bits/stdc++.h>
constexpr int N=110;
int n;
int g[N][N];
int f[N][N];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
std::cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
std::cin>>g[i][j];
memset(f,0x3f,sizeof f);
f[1][1]=g[1][1];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
f[i][j]=std::min(f[i][j],f[i-1][j]+g[i][j]);
f[i][j]=std::min(f[i][j],f[i][j-1]+g[i][j]);
}
std::cout<<f[n][n]<<std::endl;
return 0;
}三、方格取数OJ链接
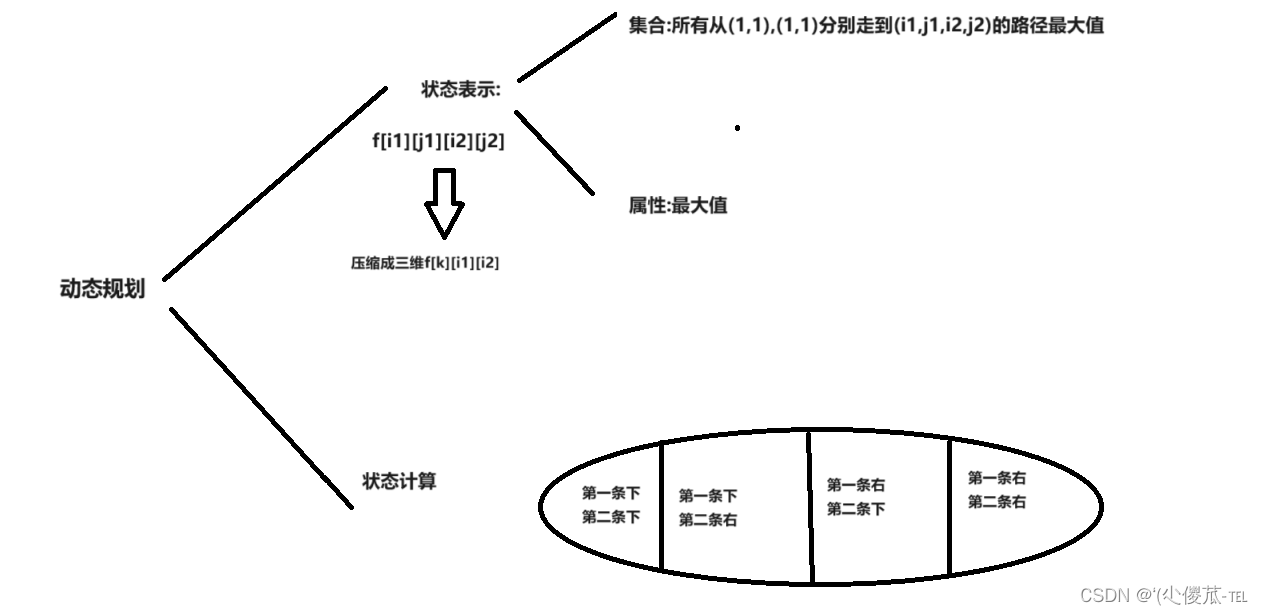
本题思路:本题中是走两次,那么状态表示:f[i1,j1,i2,j2]表示所有从(1,1),(1,1)分别走到(i1,j1),(i2,j2)的路径的最大值。由于走两次可以看成是两条路径同时走,因此k表示两条路线当前走到的各自的横纵坐标之和k == i1 + j1 == i2 + j2,注意:只有在i1 + j1 == i2 + j2时,两条路径走到的当前格子才可能重合。这里可以优化将四维状态优化成三维。
#include <bits/stdc++.h>
constexpr int N=15;
int n;
int g[N][N];
int f[N*2][N][N];//思维状态优化成三维,利用横枞坐标的和来解决
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
std::cin>>n;
int a,b,c;
while(std::cin>>a>>b>>c,a||b||c) g[a][b]=c;
for(int k=2;k<=2*n;k++)
for(int i1=1;i1<=n;i1++)
for(int i2=1;i2<=n;i2++){
int j1=k-i1,j2=k-i2;
if(j1>=1&&j1<=n&&j2>=1&&j2<=n){//边界条件
int t=g[i1][j1];
if(i1!=i2) t+=g[i2][j2];//说明此时两个点没有重合
int& x=f[k][i1][i2];
x=std::max(x,f[k-1][i1-1][i2-1]+t);//下 下
x=std::max(x,f[k-1][i1-1][i2]+t);//下 右
x=std::max(x,f[k-1][i1][i2-1]+t);//右 下
x=std::max(x,f[k-1][i1][i2]+t);//右 右
}
}
std::cout<<f[n*2][n][n]<<std::endl;
return 0;
}四、传纸条OJ链接
本题思路:本题与上面的方格取数是一样的题目。
#include <bits/stdc++.h>
constexpr int N=55;
int m,n;
int g[N][N];
int f[N*2][N][N];//思维状态优化成三维,利用横枞坐标的和来解决
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
std::cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
std::cin>>g[i][j];
for(int k=2;k<=m+n;k++)
for(int i1=1;i1<=n;i1++)
for(int i2=1;i2<=n;i2++){
int j1=k-i1,j2=k-i2;
if(j1>=1&&j1<=m&&j2>=1&&j2<=m){//边界条件
int t=g[i1][j1];
if(i1!=i2) t+=g[i2][j2];//说明此时两个点没有重合
int& x=f[k][i1][i2];
x=std::max(x,f[k-1][i1-1][i2-1]+t);//下 下
x=std::max(x,f[k-1][i1-1][i2]+t);//下 右
x=std::max(x,f[k-1][i1][i2-1]+t);//右 下
x=std::max(x,f[k-1][i1][i2]+t);//右 右
}
}
std::cout<<f[n+m][n][n]<<std::endl;
return 0;
}