目录

 克鲁斯卡尔算法

​编辑代码：

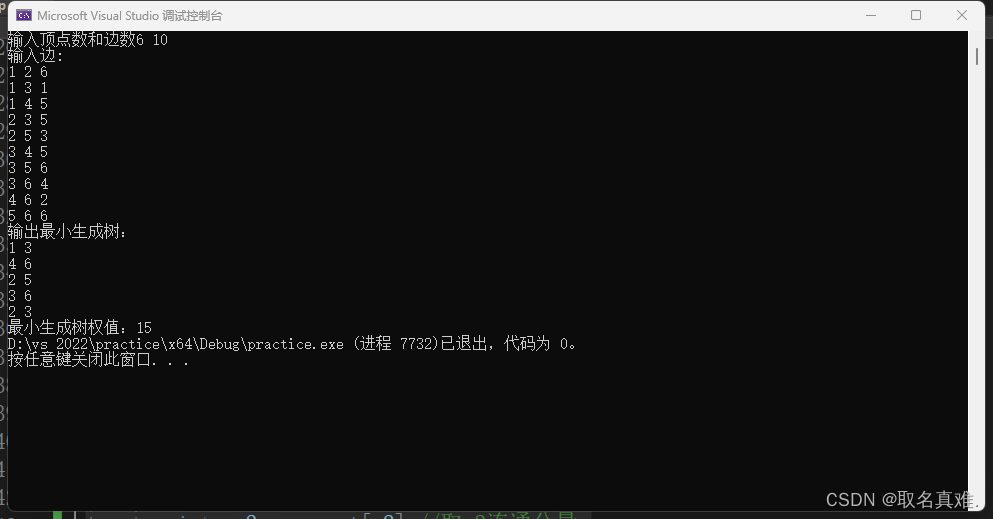
结果：

 克鲁斯卡尔算法

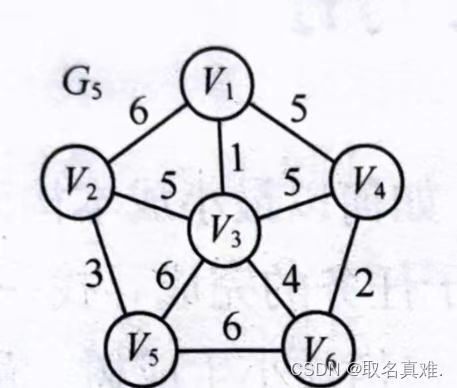
克鲁斯卡尔算法是一种用于求解最小生成树的算法。最小生成树是指一棵包含了所有节点的连通图，并且边的权值之和最小。

克鲁斯卡尔算法的基本思想是，每次选择图中最小的边，如果这条边的加入不会形成环，则将它加入最小生成树中。重复以上过程，直到所有节点都被纳入最小生成树中。

具体实现时，可以使用并查集来判断加入一条边是否会形成环。在实现过程中，需要先对边按照权值进行排序，然后遍历每条边进行判断。

代码：

#include<iostream>
#include<algorithm>
using namespace std;
typedef int vertextype;
typedef struct node
{
	vertextype head;//边起始点
	vertextype tail;//边终点
	int w;//权值
}edge;
bool cmp(edge a, edge b)//权值小的排前面
{
	return a.w < b.w;
}
int main()
{
	edge e[100];
	int n, t, vexset[100];//顶点数、边数、连通分量
	cout << "输入顶点数和边数";
	cin >> n >> t;
	for (int i = 1; i <= n; i++)//初始化连通分量
	{
		vexset[i] = i;
	}
	cout << "输入边:" << endl;
	for (int i = 0; i < t; i++)
	{
		int v1, v2, w;
		cin >> v1 >> v2 >> w;
		e[i].head = v1;
		e[i].tail = v2;
		e[i].w = w;
	}
	sort(e, e + t, cmp);
	int sum = 0;
	cout << "输出最小生成树：" << endl;
	for (int i = 0; i < t; i++)
	{
		int v1, v2;
		v1 = e[i].head;
		v2 = e[i].tail;
		int vs1 = vexset[v1];//取v1连通分量
		int vs2 = vexset[v2];//取v2连通分量
		if (vs1 != vs2)
		{
			sum += e[i].w;
			cout << v1 << " " << v2 << endl;
			for (int j = 1; j <= n; j++)//更新连通分量
			{
				if (vexset[j] == vs2)
					vexset[j] = vs1;
			}
		}
	}
	cout << "最小生成树权值："<<sum;
}

结果：