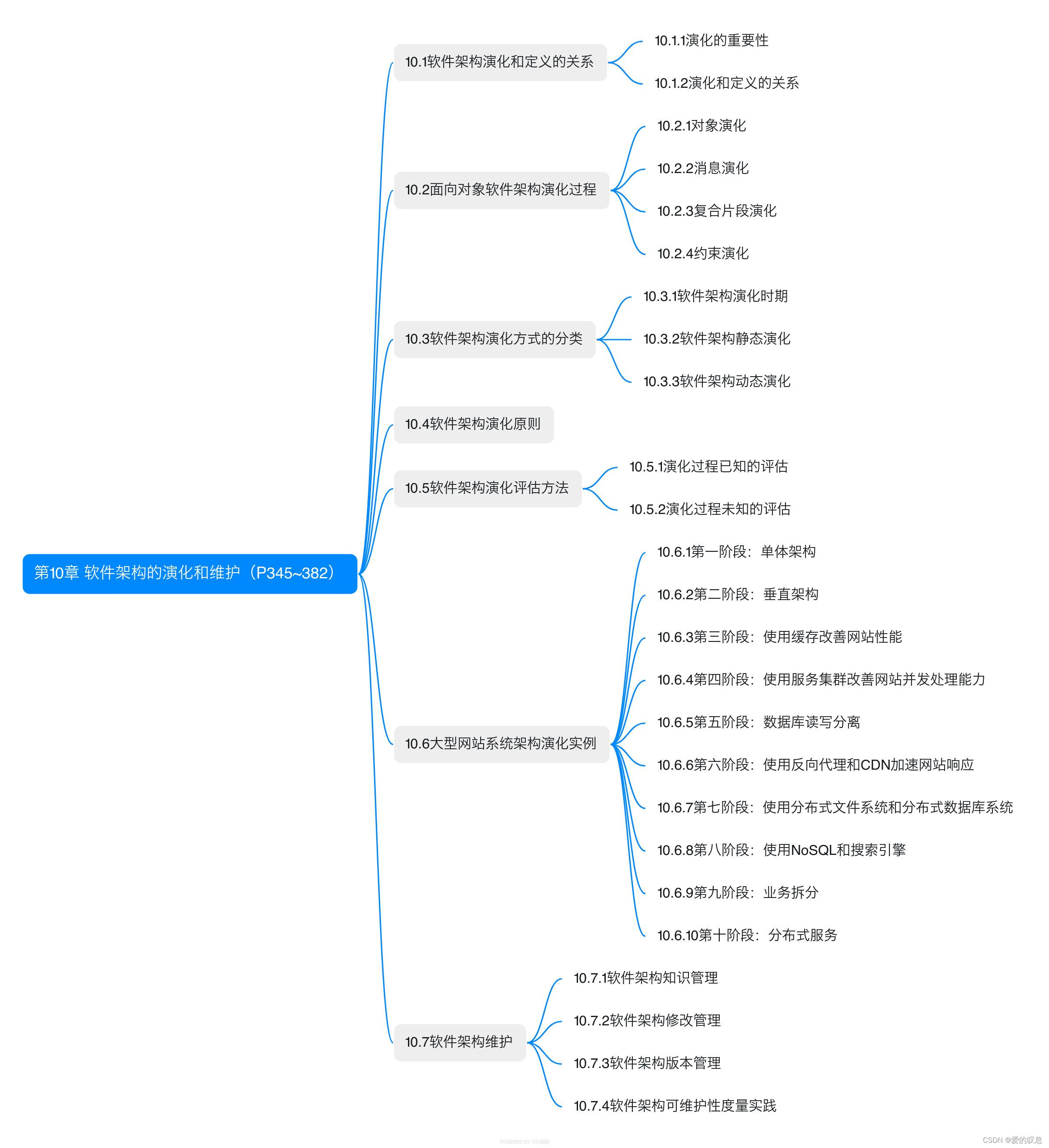
此例以说明全连接层处理图片的时候会遇到参数过多 模型过大的问题
参数比要研究的物体总数还多
卷积，特殊的全联接层
平移不变形，局部性

原本权重为二维（输入和输出全联接，想想下表组合，就是个二维的矩阵），输入输出为一维向量，可以理解为从输入和输出分别选一个节点。
现在权重变为4维，输入输出为二维矩阵，可以理解成从输入和输出分别选一个包含宽高的节点。

输入和输出都变成了二维的，权重表示使用下标，要显示输入输出的高宽，所以权重就是四维的

K阶张量与M阶张量（M<K）做内积，得到的正是K-M阶张量.

参数数量不变 保留了输入的空间信息

不对啊，一个二维的商量乘以一个四维的商量结果还是一个四维的张亮怎么得到的二维的矩阵？

对的，就是输入输出的维度变了。那么为什么要变呢？因为卷积是可以保留空间信息的，是二维的“扫”过去的，这样子二维的输入输入是可以保留一个位置的相对信息的

输入和输出都变成了二维的，权重表示使用下标，要显示输入输出的高宽，所以权重就是四维的

此时的w就是卷积核，x是图片上的某一个像素点， 乘积之后再相加，就是一个卷积的过程。

这里可以转换成4D张量，应该是因为用了batch learning，每个输入有n个样本，每个样本是一张图，一张图再转换成一个矩阵，所以隐藏层的每个神经元的权重就变成了3D张量，整个隐藏单元就成4D了

Wijkl里面的kl是对应X的kl也就是输入的矩阵的元素，ij代表卷积核里面和kl相乘的那个值，因为卷积核的值不会变但是会滑动所以sigma下标是kl，实际就是滑动卷积的意思

i,j对应filter内参数的位置，k,l是输入矩阵输入特征的位置，第一个等号说明一个Wi,j要和所有特征相乘

但参数v_{i,j,a,b} 考虑绝对位置 (i,j) 和相对位置(a,b)

根据平移不变性,我们不希望v考虑(i,j), 所以让v对(i,j)不变,只随(a,b)变

a,b两个维度代表的是之前的权重w，但是现在叫做卷积核，而i，j代表遍历每个不同的权重w使得做到滑动的效果，而去掉i，j则是代表固定卷积核，所以可以去掉i，j

这里说的意思应该是，譬如我的v是一个找猫猫的特征器，这个识别猫特征器不会因为图片中猫藏的位置不一样而变化

平移不变性，其实就是代表我这个卷积核提取的特征是固定的，我一个卷积核只要参数不变，从一张图里面提取的特征就是不变的

平移不变性是卷积过程中卷积核不变，共享同一组权重，局部性是指不考虑整个图像，仅计算当前2*2的窗口。这个窗口有一个官方名称为感受野

神经网络去学一些核来得到想要的输出
边缘检测，锐化，模糊

高斯模糊就是平均池化嘛

卷积核肯定是自己学，因为卷积核中每个元素都代表一个weight

卷积核：有正有负和为0是边缘检测

全为正和为1是均值滤波，高斯权重的均值滤波是高斯平滑/模糊

是不是说卷积时他的核需要逆时针旋转180°，相关不需要

cnn中的卷积核旋转180度就是数学上的卷积

不是180度是水平竖直翻转，沿着副对角线做对称翻转。左右上下反一下

如果不懂为什么是负号的，可以去看王木头学科学关于卷积的视频

说通信卷机和这里根本不一样的，我觉得你卷积根本没理解，这就是一样的，只是少了一个负号，其实本质一样，都是一个滤波器，只是这里的滤波器可以通过神经网络学习

矩阵乘法是每行每列都做点积，得到的是矩阵，矩阵中每个元素都是行列的点积。
哈达玛积就是对应位置元素乘积，没有求和，得到的也是矩阵

卷积需要将那个核旋转180°获得

kernel_size是一个向量：[k_h,k_w]，它表示卷积核的大小/维数

不一定，比如阿尔法狗卷积核就不是矩形
竖直边缘，黑变白还是白变黑

其实这个矩阵为什么可以做垂直检测，可以去找opencv课程，里面需要接触一些xx算子，会详细解释为什么这种矩阵可以提取边缘图像

通道维：通道数，RGB图3通道，灰度图1通道，批量维就是样本维，就是样本数

反了！前面是批量维，后面是通道维度

（批量大小、通道、高度、宽度）
手写训练逻辑，迭代十次

前面的说错了吧？谁告诉你Y是随机给的？Y是前面用[1,-1卷积出来的结果，并不是随机给的]

这里直接用了梯度下降，没有考虑优化

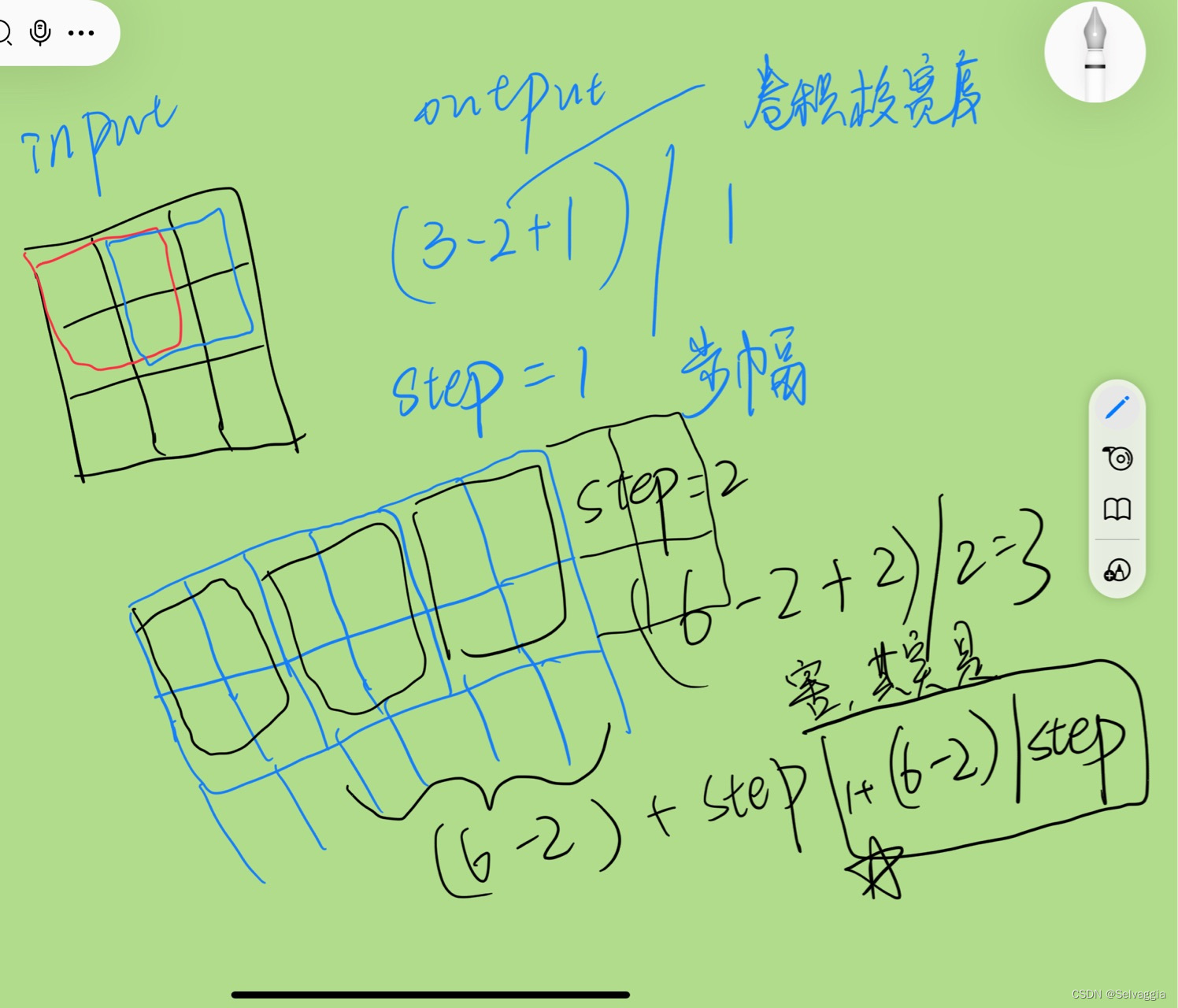
6,8是X的形状；1,2是K的形状；Y的形状就能推出来是(6-1+1,8-2+1)即(6,7)

每加一层输入大小减去4（5-1）

数据量大的时候，这点损失不影响

本质就是信息有损压缩啊

下图不重要但强迫症偏要扪清这加减运算