在spss统计分析中,方差分析在比较均值菜单和一般线性模型菜单中都可以做,单因素方差分析一般称为单因素Anova分析,单变量方差分析一般称为一般线性模型单变量分析。这两种方法既有区别又有联系,在统计学中,这两种分析方法统称为方差分析,在spss中由于线性模型的引入,才有所区分,那么这两种分析方法在具体应用中有什么样的区别和联系?二者的适用情况是什么?分析结果有何异同?下面将进行详细介绍。
一、【基本概念】
- 方差分析(analysisof variance,Anova)是对总体均值的比较,其目的是检验平均值之间的差异是否具有统计学意义。
- 单因素方差分析(One-wayAnova),是检验由单一因素影响的多组样本某因变量的均值是否有显著差异。与之对应的是多因素方差分析,需要说明的是:这里的单因素与多因素是针对自变量而言的,因变量可以有多个,但只有一个自变量(spss里称为因子)。
- 单变量方差分析: 即单因变量方差分析,单变量对应的英文名称为“univariate”,其实际含义是“只有一个因变量的方差分析模型”,是检验几个分类变量对单个因变量均值的影响。与之相对应的是多变量方差分析。需要说明的是:这里的自变量(spss里称为因子,又包括固定因子和随机因子)可以有多个,但只有一个因变量。
二、【SPSS实现】
2.1 案例分析
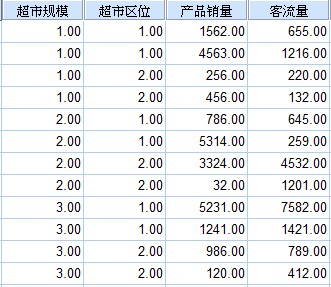
某公司生产某种新食品,在不同区域内随机选取不同规模的超市,进行销售(具体数据见下图),要求分析超市规模对该产品销量的影响;
2.2 分析思路
案例中有两个自变量即超市规模(大、中、小,分别用1,2,3表示)和超市区位(市区、乡下,分别用1,2表示);两个因变量,即产品销量和客流量。如果要研究超市规模对产品销量的影响,那么这里的自变量就只有一个,即超市规模(三种水平,大、中、小),因变量也只有一个,即产品销量。因此,本例可以使用单因素方差分析法,也可以使用单变量方差分析法。
我们同时采用这两种方法进行分析,对比一下这两种分析方法的结果有何异同。
2.3 分析步骤
(1)单因素方差分析
- 选择菜单【分析】-【比较均值】-【单因素Anova】,在弹出的对话框中进行如下选择:把【产品销量】选入因变量列表框,把【超市规模】选入因子列表框。从这里可以看出,因变量列表框是可以选择多个因变量的,但是因子列表框中,只能选择一个变量。

2.在右侧选择【事后多重比较】菜单,进行如下操作:勾选【LSD】、【SNK】、【Bonferroni】、【Tukey】、【Duncan】复选框,单击【继续】按钮,返回主对话框。(方法的选择主要依据想要何种多重比较结果,一般以选择LSD\TUKEY\SNK\SCHEFFE居多,Bonferroni法是对LSD法的改进,这里为了进行不同方法间的比较,故选以上方法)。此对话框对应的是均值的多重比较,主要分为假定方差齐性和未假定方差齐性两类,基本上只使用假定方差齐性,因为如果方差不齐性,不建议做方差分析或进行两两比较。

3.在右侧选择【选项】菜单,依次勾选【描述性】、【方差同质性检验】、【平均值图】,其他默认,单击【继续】按钮,返回主对话框。其中方差同质性检验即方差齐性检验,检验不同规模超市之间的产品销量的方差是否齐性。因为方差齐性与否直接决定着进行多重比较时的方法选择。
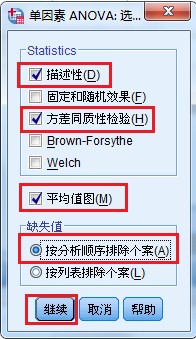
4.单击【确定】按钮,输出结果。

(2)单变量方差分析
1.选择菜单【分析】-【一般线性模型】-【单变量】,在弹出的对话框中进行如下选择:把【产品销量】选入因变量列表框,把【超市规模】选入固定因子列表框。需要注意的是:这里的【因变量】列表框只能选择一个变量,【固定因子】、【随机因子】列表框可以选择多个变量。
从对话框可以看出单变量方差分析与单因素方差分析的差别:一般线性模型单变量方差分析的因子区分为固定因子和随机因子,比单因素Anova分析更为细致,而且固定因子列表框可以同时选入多个变量,单因素Anova分析,因子列表框只能选入一个变量。

2.在主对话框界面选择右侧【模型】菜单,选择默认【全因子】,【类型Ⅲ】,单击【继续】按钮返回主对话框

3.在主对话框界面右侧选择【事后多重比较】菜单,把【超市规模】选入【事后检验】列表框,同样勾选【LSD】、【SNK】、【Bonferroni】、【Tukey】、【Duncan】复选框,单击【继续】按钮,返回主对话框。该对话框与单因素Anova对话框类似,但不同的是这里可以自由选入因子。

4. 在主对话框界面右侧选择【选项】菜单,在【输出】栏,勾选【描述性统计】【同质性检验】、【残差图】复选框,单击【继续】按钮返回主对话框

5. 单击【确定】按钮,输出结果。

-
2.4 结果解释
(1)单因素Anova分析结果解释
1.描述性统计结果
下图输出了基本的样本量、平均值、标准差等描述性统计结果。可知,较大规模超市的平均销量是最高的,但这只是针对该样本的,其所在总体是否也如此,需要进行后续分析。
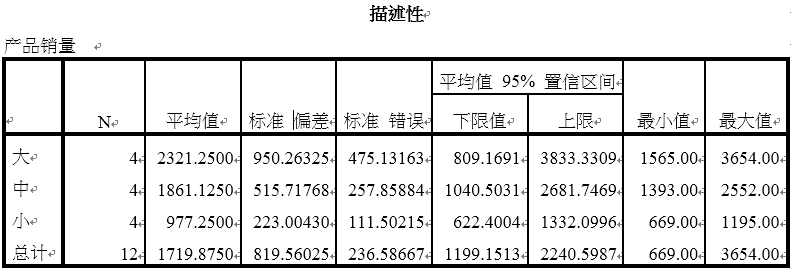
2.方差同质性检验结果
下图输出了方差同质性检验结果,方差同质性检验采用的是levene检验,检验3种超市规模之间的方差是否齐性,由表中显著性=0.165>0.05可知,接受原假设,认为3种超市规模之间方差相等。
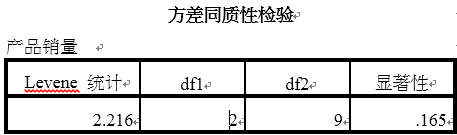
3.方差分析结果
方差分析采用的是F检验,表中,平方和表示离差平方和,也就是变异,分为组间变异、组内变异。Df为自由度,均方为离差平方和/自由度,F统计量=组间均方/组内均方。其显著性=0.042<0.05,故拒绝原假设,认为不同超市规模之间的均值具有显著差异(由于显著性=0.042,说明是弱显著性)。具体是哪种规模之间有均值有显著差异,故需要再进一步做多重比较分析。
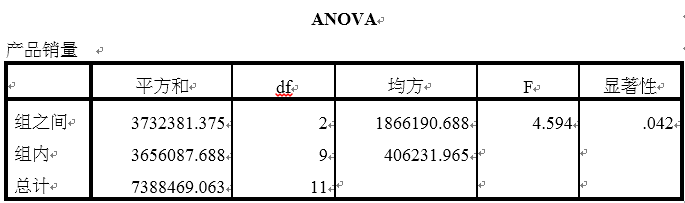
4.事后检验结果
下图输出了【LSD】、【Bonferroni】、【Tukey】法的分析结果,可以看出,规模较大超市与较小超市之间差异显著,中等规模超市与较大规模超市和较小规模超市之前均不存在显著差异。三种比较方法的结果一致。

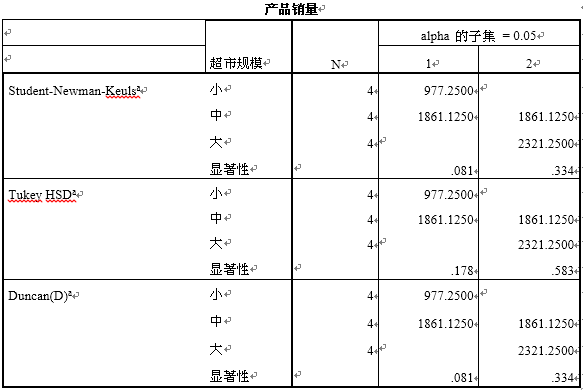
5.同类子集
下图为同类子集输出结果,Student-Newman-Keuls,Tukey,Duncan(D)三种方法的思想,都是在样本中寻找同质的组,认为同组的水平没有差异,从结果可以看出,三种方法都把规模分为两组,小中一组,中大一组,因此可以排除中等规模的影响,认为较小规模与较大规模之间均值存在显著差异。
6.平均值图
从3种规模超市之间的销量均值图也可以看出三种规模之间的差异。

(2)一般线性模型单变量结果解释
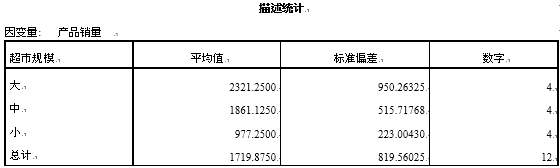
1.描述统计结果
同样输出了三种规模超市的平均值、标准差、样本量等情况,可以看出较大规模超市的平均销量较高,同时其标准差也较大。
2.方差齐性检验
由下图可以看出,显著性=0.165>0.05,与单因素Anova分析结果一致,不能拒绝原假设,认为三种水平的方差相等。

3.方差分析结果
- 第1行,校正的模型,是对整个方差分析模型的检验,原假设为模型中所有因素对因变量无影响,即μ=0,此处p<0.05,即均值不等于0,拒绝原假设,即认为超市规模对产品销量有影响。
- 第2行,截距,原假设为不考虑自变量影响时,因变量的均值为0,此处P<0.05,拒绝原假设。
- 第3行,超市规模,也就是对自变量的检验即组间变异,原假设为自变量对因变量没有影响,此处P<0.05,拒绝原假设。可以看出此处的结果同第1行的结果是相同的,这是因为案例只涉及到单一变量(产品销量)的比较。
- 第4行,错误即误差
- 第5行,总计=截距+组间+误差
- 第6行,校正=组间+误差

4.事后检验
同样,下图输出了【LSD】、【Bonferroni】、【Tukey】法的分析结果,可以看出,规模较大超市与较小超市之间差异显著,中等规模超市与较大规模超市和较小规模超市之前均不存在显著差异,三种比较方法的结果一致。该结果与单因素Anova方法一致。

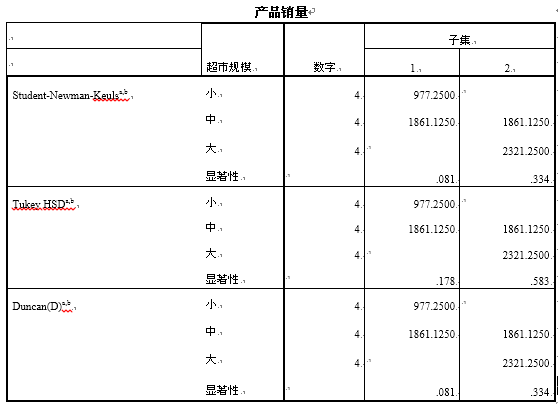
5.均一子集
下图为均一子集输出结果,Student-Newman-Keuls,Tukey,Duncan(D)三种方法的分析结果与单因素Anova分析结果一致。
三、【总结】
- 单因素方差分析和单变量方差分析的区别主要体现在在前者是单个自变量,后者是单个因变量。在实际运用中,这两种方法的统计效能是等价的,一般不做特别严格的区分,只是一般线性模型比单因素在某些方面更为细致一些。
- 在适用条件上,二者的条件相同,均为:独立性、正态性、方差齐性。