代码随想录算法训练营第五十四天丨动态规划part15

392.判断子序列

思路

（这道题也可以用双指针的思路来实现，时间复杂度也是O(n)）

这道题应该算是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

所以掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础。

动态规划五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。

为啥要表示下标i-1为结尾的字符串呢，为啥不表示下标i为结尾的字符串呢？

为什么这么定义卡哥在 718. 最长重复子数组 (opens new window)中做了详细的讲解。

其实用i来表示也可以！

但我统一以下标i-1为结尾的字符串来计算，这样在下面的递归公式中会容易理解一些，如果还有疑惑，可以继续往下看。

确定递推公式

在确定递推公式的时候，首先要考虑如下两种操作，整理如下：

if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
if (s[i - 1] != t[j - 1])
- 相当于t要删除元素，继续匹配

if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因为找到了一个相同的字符，相同子序列长度自然要在dp[i-1][j-1]的基础上加1（如果不理解，在回看一下dp[i][j]的定义）

if (s[i - 1] != t[j - 1])，此时相当于t要删除元素，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];

其实这里大家可以发现和 1143.最长公共子序列 (opens new window)的递推公式基本那就是一样的，区别就是本题如果删元素一定是字符串t，而 1143.最长公共子序列是两个字符串都可以删元素。

dp数组如何初始化

从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。

这里大家已经可以发现，在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

因为这样的定义在dp二维矩阵中可以留出初始化的区间，如图：

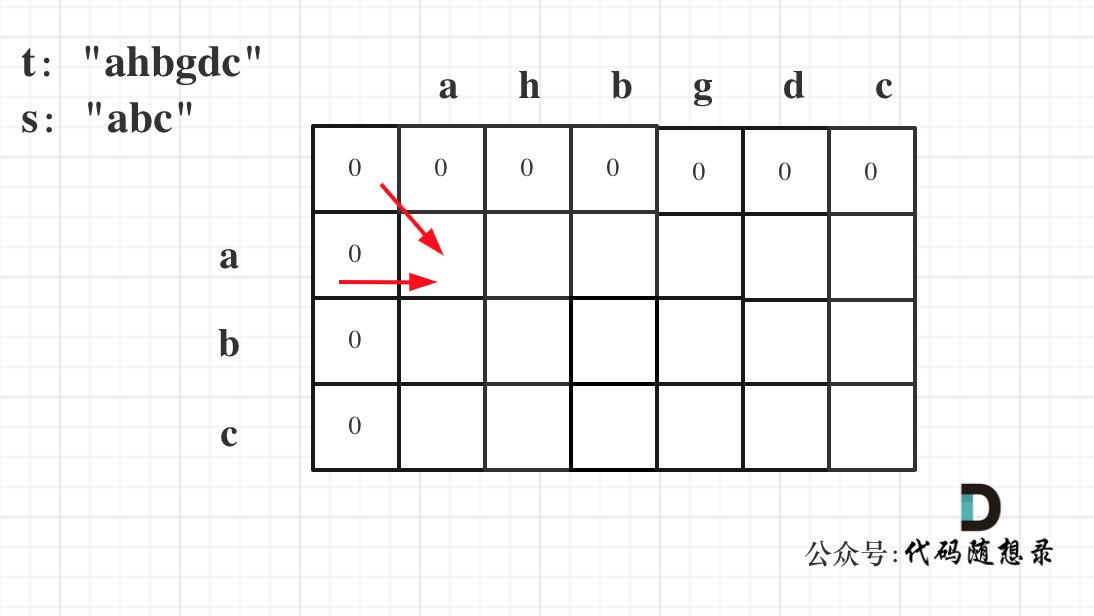
392.判断子序列

如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t，初始化就比较麻烦了。

dp[i][0] 表示以下标i-1为结尾的字符串，与空字符串的相同子序列长度，所以为0. dp[0][j]同理。

int[][] dp = new int[t.length()+1][s.length()+1];

确定遍历顺序

同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右

如图所示：

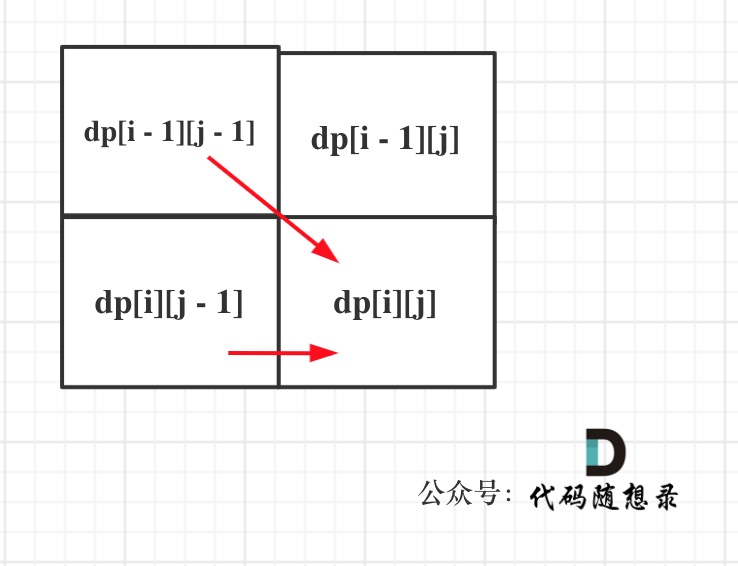
392.判断子序列1

举例推导dp数组

以示例一为例，输入：s = "abc", t = "ahbgdc"，dp状态转移图如下：

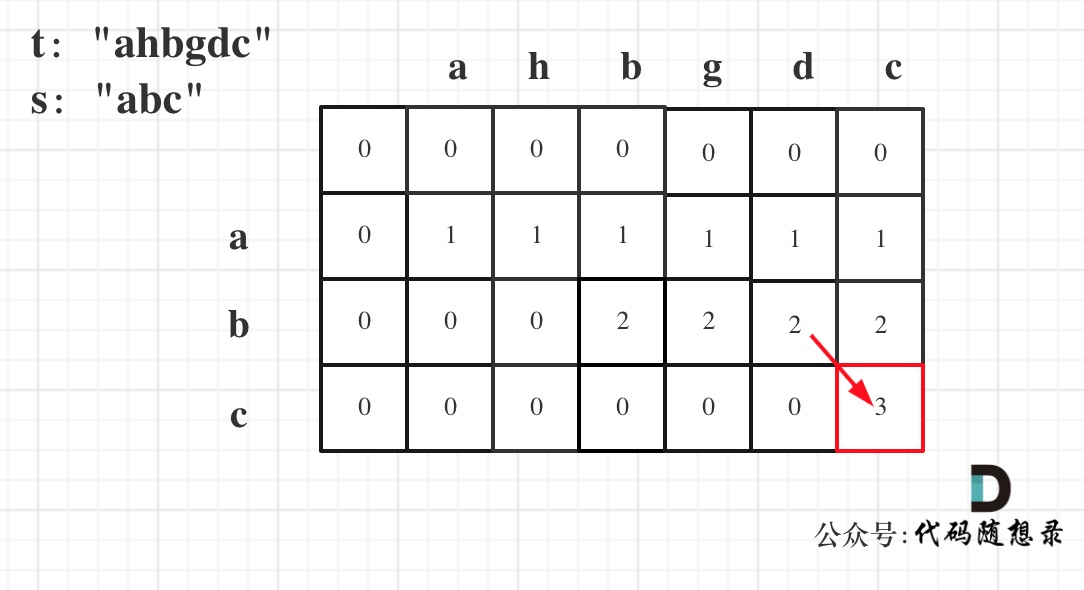
392.判断子序列2

dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度，所以如果dp[s.size()][t.size()] 与字符串s的长度相同说明：s与t的最长相同子序列就是s，那么s 就是 t 的子序列。

图中dp[s.size()][t.size()] = 3，而s.size() 也为3。所以s是t 的子序列，返回true。

动规五部曲分析完毕，C++代码如下：

class Solution {
    public boolean isSubsequence(String s, String t) {
        int[][] dp = new int[t.length()+1][s.length()+1];
        for (int i = 1; i <= t.length(); i++) {

            for (int j = 1; j <= s.length(); j++) {
                if (s.charAt(j-1) == t.charAt(i-1)){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else {
                    dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[t.length()][s.length()] == s.length() ? true : false;
    }
}

时间复杂度：O(n × m)
空间复杂度：O(n × m)

115.不同的子序列

思路

这道题目如果不是子序列，而是要求连续序列的，那就可以考虑用KMP。

这道题目相对于72. 编辑距离，简单了不少，因为本题相当于只有删除操作，不用考虑替换增加之类的。

但相对于刚讲过的动态规划：392.判断子序列 (opens new window)就有难度了，这道题目双指针法可就做不了了，来看看动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

为什么i-1，j-1 这么定义卡哥在 718. 最长重复子数组 (opens new window)中做了详细的讲解。

确定递推公式

这一类问题，基本是要分析两种情况

s[i - 1] 与 t[j - 1]相等
s[i - 1] 与 t[j - 1] 不相等

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。

一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。

这里可能有录友不明白了，为什么还要考虑不用s[i - 1]来匹配，都相同了指定要匹配啊。

例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。

当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。

所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1][j]

所以递推公式为：dp[i][j] = dp[i - 1][j];

这里可能有录友还疑惑，为什么只考虑 “不用s[i - 1]来匹配” 这种情况，不考虑 “不用t[j - 1]来匹配” 的情况呢。

这里大家要明确，我们求的是 s 中有多少个 t，而不是求t中有多少个s，所以只考虑 s中删除元素的情况，即不用s[i - 1]来匹配的情况。

dp数组如何初始化

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来，如图：，那么 dp[i][0] 和dp[0][j]是一定要初始化的。

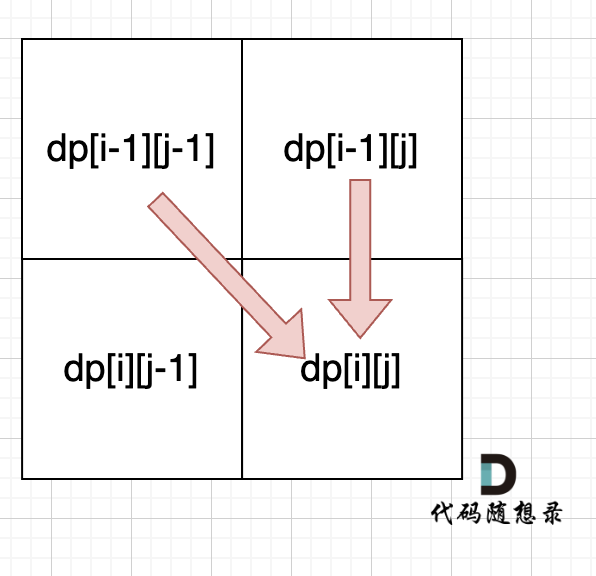
每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。

dp[i][0]表示什么呢？

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。

dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

初始化分析完毕，代码如下：

int[][] dp = new int[s.length() + 1][t.length() + 1];
for (int i = 0; i < s.length(); i++) {
    dp[i][0] = 1;
}

确定遍历顺序

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。

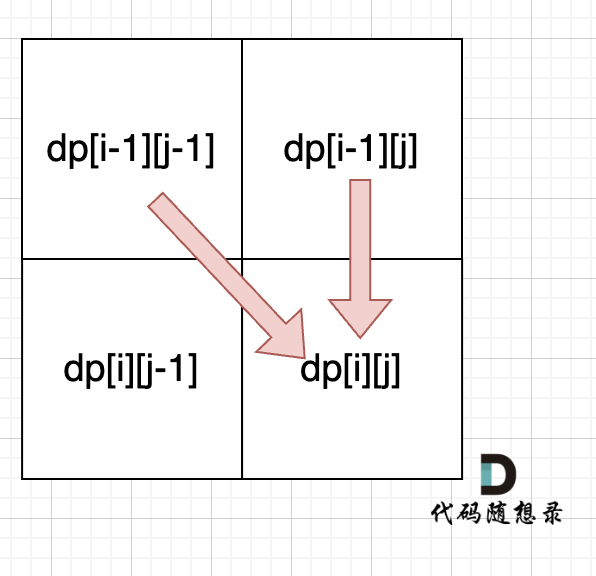
所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算。

代码如下：

 for (int i = 1; i <= s.length(); i++) {
     for (int j = 1; j <= t.length(); j++) {
         if (s.charAt(i - 1) == t.charAt(j - 1)) {
             dp[i][j] = dp[i - 1][j - 1] + dp[i-1][j];
         }else {
             dp[i][j] = dp[i-1][j];
         }
     }
 }

举例推导dp数组

以s："baegg"，t："bag"为例，推导dp数组状态如下：

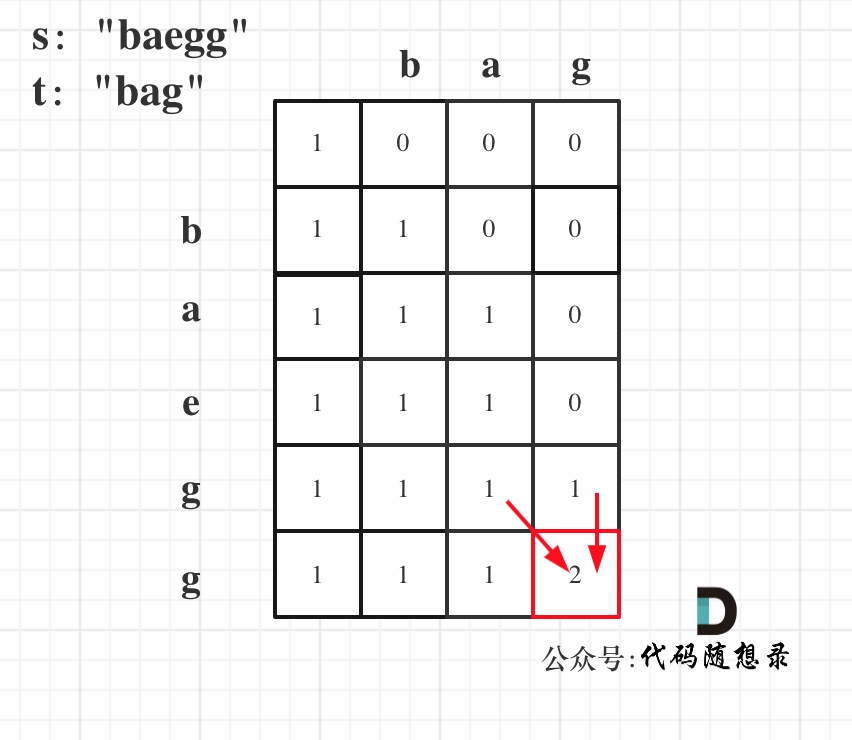
115.不同的子序列

如果写出来的代码怎么改都通过不了，不妨把dp数组打印出来，看一看，是不是这样的。

动规五部曲分析完毕，代码如下：

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];

        for (int i = 0; i < s.length(); i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= t.length(); j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i-1][j];
                }else {
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}

时间复杂度: O(n * m)
空间复杂度: O(n * m)