电路综合-基于简化实频的集总参数电路匹配1
对于分布式参数的匹配方法,我们已经深入探讨并给出了解决方案:
10、电路综合-基于简化实频的宽带匹配电路设计方法
{阻抗匹配其实就是S11电路的匹配,给定需要匹配的阻抗数值去设计微带电路,其实就是给定了部分频点的S11参数去综合出电路图。我们唯一需要的就是根据部分频点的S11参数去拟合S11在理查德域的解析表达式。 这个拟合过程也可以看为一个优化过程,是为了使得解析表达式尽可能的接近已知的S11参数。其基本过程和9、电路综合-基于简化实频的任意幅频响应的微带电路设计一致。}
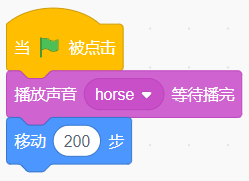
但是,对集总端口的匹配问题,相比并不简单。例如,对于下面的拓扑,我们如何将其匹配至1欧姆的归一化端口?
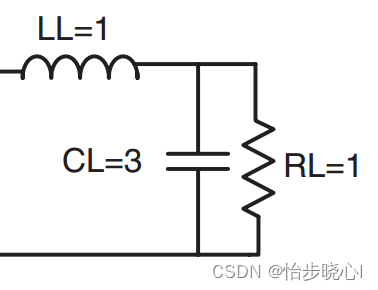
一种简单的方法是将其视为切比雪夫滤波器中的一部分,例如下图:
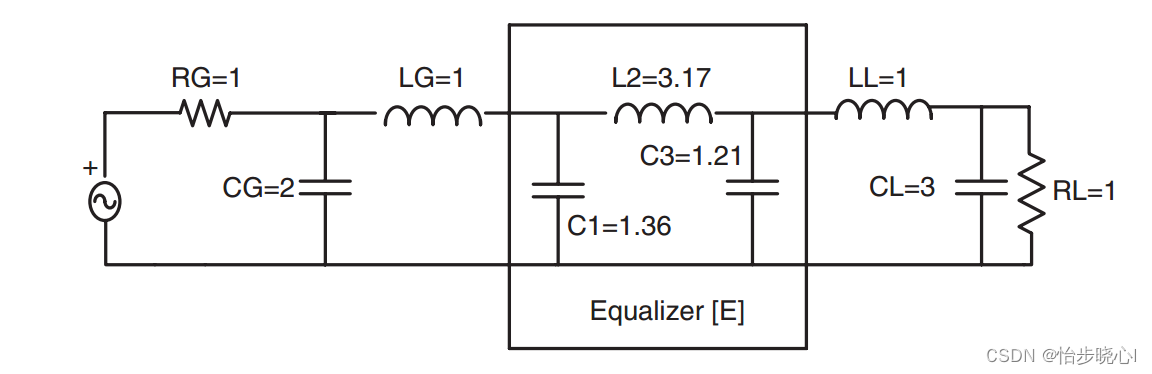
这种匹配方法非常简单,但是有很大的限制范围。首先,要进行匹配的结构必须是Causer形式的;其次,为了契合切比雪夫的多项式,有些参数无法严格对应;
下面介绍一种基于实频的直接综合方法,可以对任意结构的拓扑进行匹配电路的计算综合。
1、计算给定负载的阻抗特性
具体的计算过程参考如下链接:
11、电路综合-集总参数电路结构的S参数模型计算与Matlab
教程简介:对于实际的电路,我们可能不会使用纯微带电路进行实现(很多模型的寄生参数往往都会等效为集总参数),可能需要用到集总参数和分布参数混合的方式,此文章介绍了集总参数电路综合的基本理论(输入阻抗计算、S11参数计算)。
此处,我们只需要得到给定负载的策动点阻抗函数Z即可。
给出简单的计算代码示例(对应电容电阻并联、电感串联的结构,p就是Laplace s):
p=sqrt(-1)*w;
YL=(1/R)+C*p;
ZL=p*L+1/YL;
RL=real(ZL);
XL=imag(ZL);
对于基于简化实频的匹配方法,我们并不需要整个频域的阻抗情况,例如,如果我们需要在角频率w=[0,1]的范围内进行匹配,只需要在[0,1]的范围内取几个离散点即可。当然,如果要匹配的负载不是具体的集总参数的形式,只要能给出不同频率下对应的阻抗,也能基于此方法进行匹配电路的综合。
2、优化的初始值的生成
给出一个传输增益的计算方程,其中B下标的是需要设计的匹配电路的策动点阻抗的虚部与实部。可以知道,如果能够抵消电抗部分,就可以获得最高的传输增益。
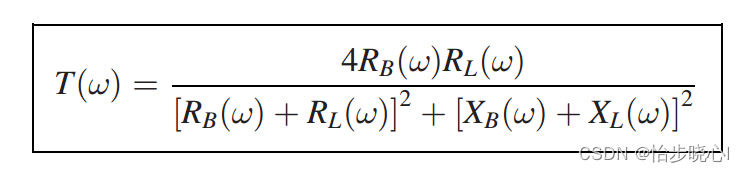
在此,我们假设电抗部分被抵消,则此时的匹配电路的阻抗实部可用下式计算(需要先设定预期的功率增益T0):
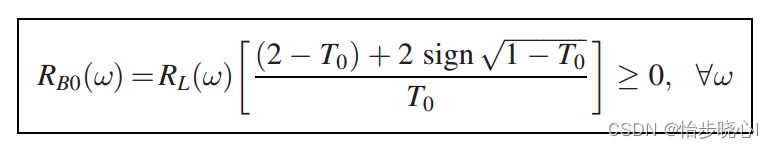
匹配电路的阻抗虚部就是实部的希尔伯特变换(对于最小阻抗函数)。计算得出的匹配电路的阻抗实部可以作为非线性优化的初始值,因为这是在假设抵消电抗部分情况下得出的结果。
3、基于初始值进行优化
将匹配电路的实部作为优化参数,匹配电路的阻抗虚部就是实部的希尔伯特变换。其初始值设定为上述计算得出的RB0。使用Matlab的lsqnonlin函数进行非线性优化。
优化结果即为最佳的匹配电路的实部,从而使用希尔伯特变换计算得出阻抗虚部。主要,此处得到的都是数值解,并非解析表达式。可以基于此数值对匹配结果进行初步的估算。
4、Matlab的代码实现
clear
clc
close all
% 分析的计算点数 越多越精密
N=21;
% 设定要匹配的负载参数
R=1;
C=3;
L=1;
% 匹配范围0-1,分析截至频率1.2
wc1=0;
wc2=1;
ws1=0;
ws2=1.2;
% 理想增益设定为0.8
T0=0.8;
% 使用阻抗函数进行综合
KFlag=1;
% sign为+-1,结构不同
sign=1;
% Step 1: Generate the load data
WBR=Break_Frequencies(N,ws1,ws2,wc1,wc2);
for i=1:N
w=WBR(i);
[RL,XL]=RLC_Load(w,R,C,L,KFlag);
RLA(i)=RL;XLA(i)=XL;
end
% Step 2: 计算出RB0的初始值
RB0=initials(R,C,L,KFlag,T0,sign,WBR);
XB0=Hilbert_Transform(WBR,RB0);
% Step 3: 进行优化
% Define unknowns for the optimization:
for j=1:(N-1)
x0(j)=(RB0(j));%Initial
end
OPTIONS=optimset('MaxFunEvals',20000,'MaxIter',50000);
x=lsqnonlin('error_RFLT',x0,[],[],OPTIONS,WBR,wc1,wc2,N,T0,R,C,L,KFlag);
% Generate optimized driving point impedance
for j=1:N-1
RBA(j)=x(j);
end
RBA(N)=0.0;
XBA=Hilbert_Transform(WBR,RBA);
% 画图
RTSQ=(RB0+RLA).*(RB0+RLA);
XTSQ=(XB0+XLA).*(XB0+XLA);
TPG0=4*RLA.*RB0./(RTSQ+XTSQ);
RTSQ=(RBA+RLA).*(RBA+RLA);
XTSQ=(XBA+XLA).*(XBA+XLA);
TPG=4*RLA.*RBA./(RTSQ+XTSQ);
figure
plot(WBR,TPG,WBR,TPG0)
xlabel('Angular Frequency')
ylabel('Optimized Gain')
title('OPtimized Gain Plot')
legend('经过lsqnonlin优化的结果','RB0的初始值得出的增益结果')
运行结果(可见优化后的结果更能满足设计要求):
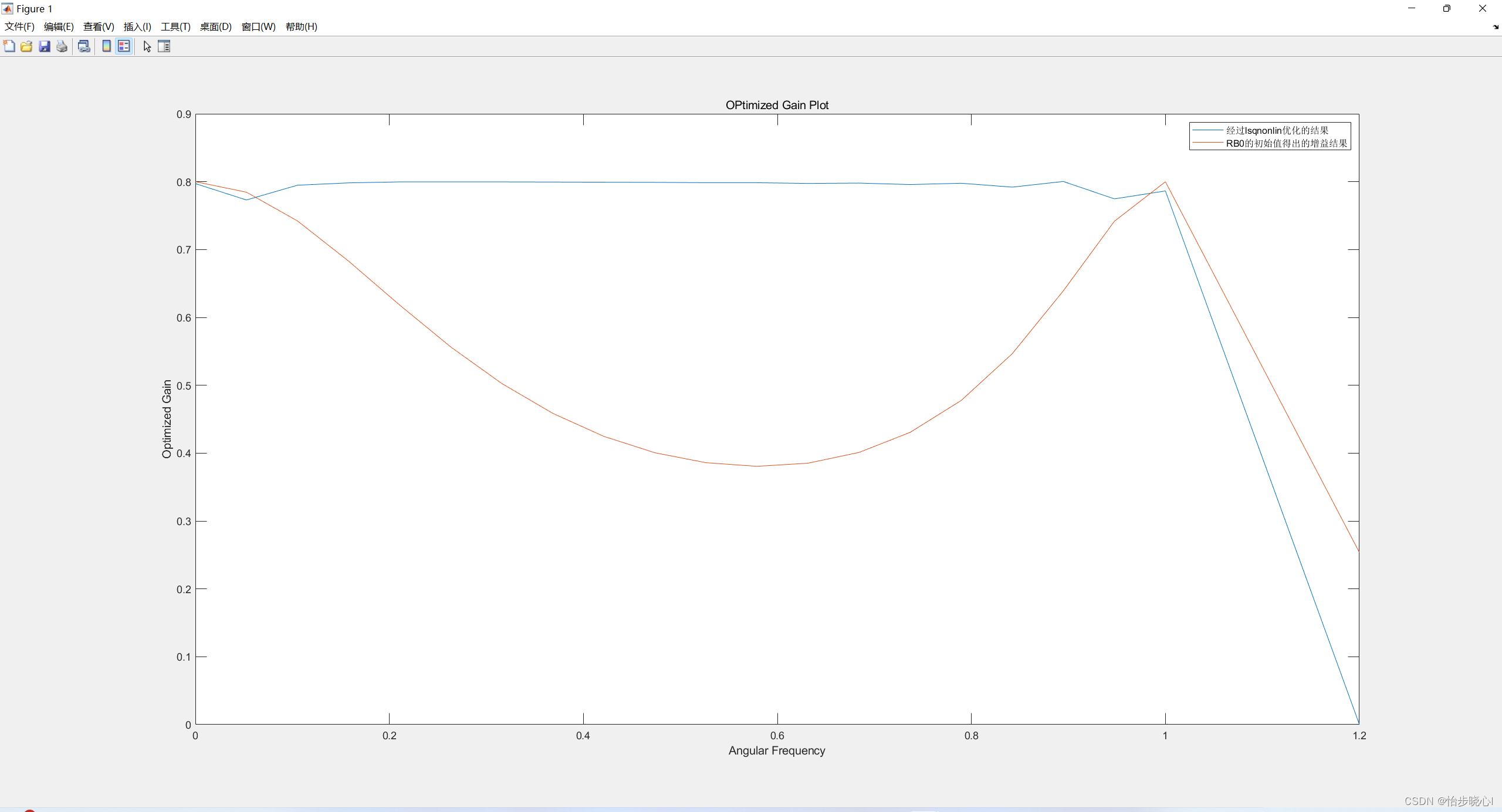
在上面的分析中,我们设定理想的功率增益为0.8,为什么不是1呢?因为这是出于平坦度的考虑,可能对于所给出的负载端,不存在任何电路能够实现这么理想的匹配。例如,如果将增益设为1,得出的结果为:
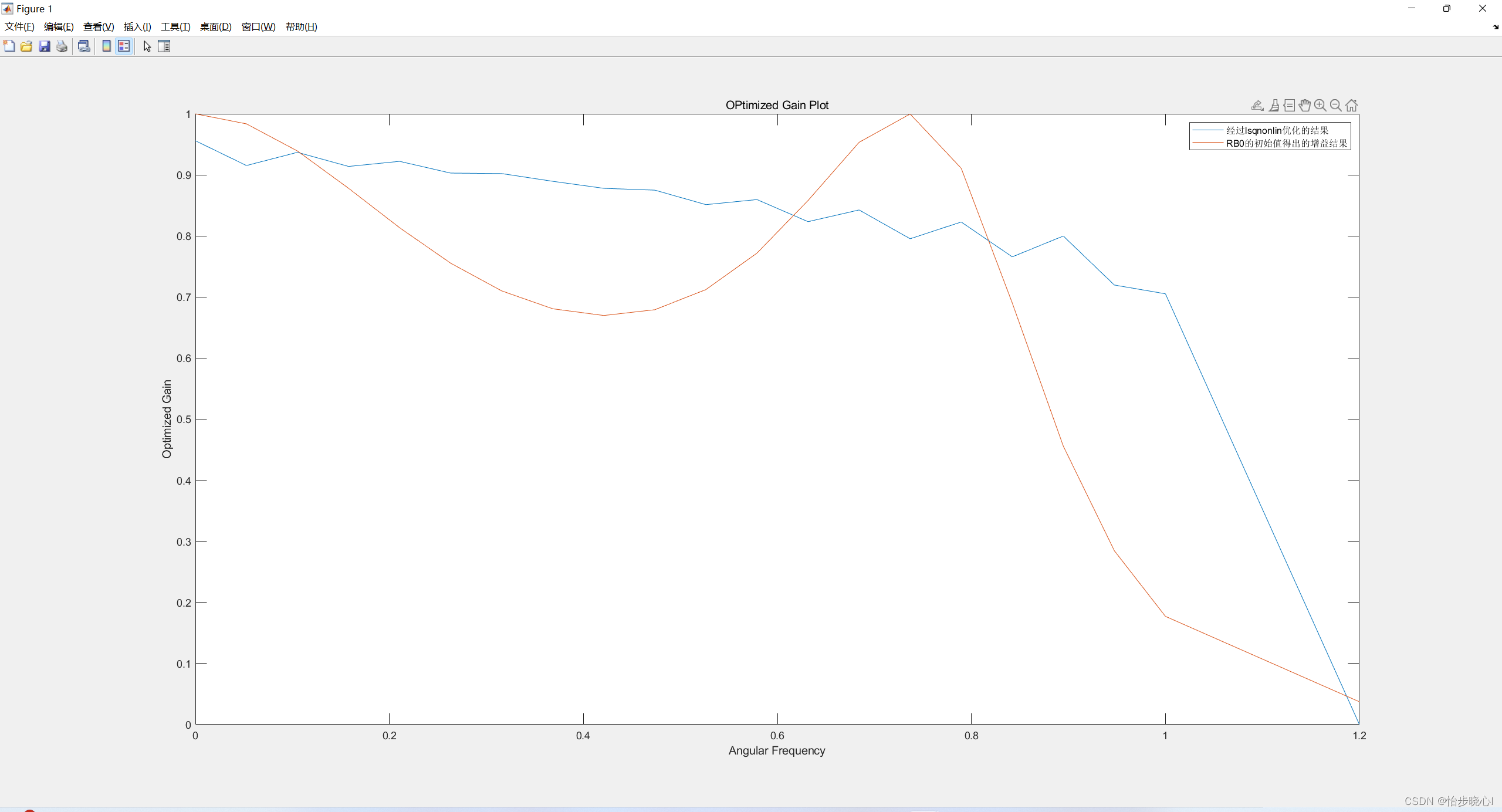
明显,在低频处效果更好,但是高频处性能不佳,且不够平坦。
注意,到此为止我们只得到了要设计的匹配结构的数值型的策动点阻抗,需要将其转化为Laplace域的解析形式再进行电路综合才能得到具体的电路拓扑。下面我们将介绍此过程。