【Mquant】7：构建价差套利(三) —

文章目录

1. 上节回顾
2. 纯碱价差套利
3. 什么是协整性分析
4. 通过协整性检验
5. 空间误差校正模型（VECM）
6. 构建交易策略
7 总结

1. 上节回顾

【Mquant】6：构建价差套利(二)上节带领大家编写了统计套利均值回归的程序，通过历史回测发现还不能进入实盘交易状态，原因出现在手续费率上，由于加密市场手续费率较高，我们选择国内期货市场，一般期货市场手续费率可以达到万分之一，个别品种手续费率可以达到万分之0.1。这节内容，我们围绕期货产品中的纯碱来做统计套利。纯碱一手交易所收取3.5元手续费，期货公司在这个基础上收取+1分的开户手续费也就是一手3.51元。

2. 纯碱价差套利

纯碱价差套利是一种商品套利策略，涉及到纯碱市场中不同地区或不同时间点的价格差异。纯碱是一种广泛用于工业和化工生产的碱性物质，其价格受到供需关系、运输成本、市场地区等因素的影响。

纯碱价差套利的基本原理是在不同市场或时间点购买低价的纯碱，然后在高价的市场或时间点出售，从价格差异中获得利润。这种套利策略依赖于市场价格的波动以及供需不平衡的情况，因此需要及时准确地识别价格差异和执行交易。建议在实施任何套利策略之前，咨询专业人士或金融顾问，以获得适当的建议和指导。

郑商所仓单交割相关规定：
http://www.czce.com.cn/cn/flfg/zcjywgz/pzxz/webinfo/2023/05/1685047755429516.htm

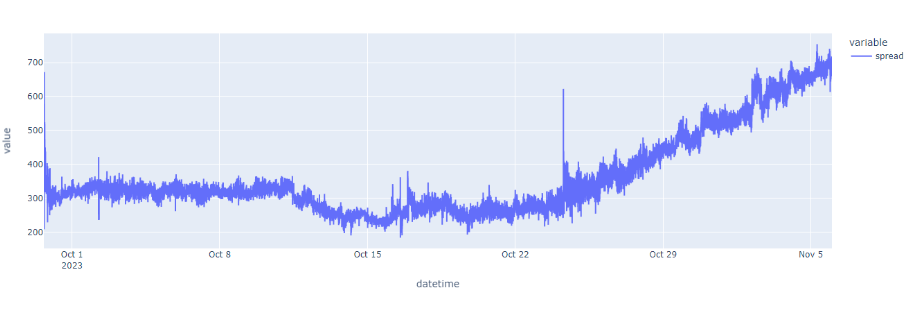
【Mquant】5：构建价差套利(一) 中：我们描述了价差走势曲线，从图中可以很清晰的看出在某一段时间内，两个合约价差比较平稳，如2023年10月1日到10月10日，在2023年10月22日后，价差走了一波上涨趋势，对于这种非平稳的时间序列，我们就很难去做价差均值回归策略。于是在【Mquant】6：构建价差套利(二)中我们通过价格波动率指标去选择交易品种，并且构建了一个布林带交易策略，但是受到手续费和价差的影响，实际策略并不能赚钱。这节内容我们深入探讨“平稳性”这个概念，带领读者通过协整性分析，找到一组资产的价格在长期内存在稳定的线性关系，来优化交易策略。
在这里插入图片描述

3. 什么是协整性分析

用学术的话讲：协整性分析是一种用于检验非平稳时间序列之间是否存在稳定关系的方法。它可以帮助我们确定变量之间的长期均衡关系，以及是否存在伪回归的情况。

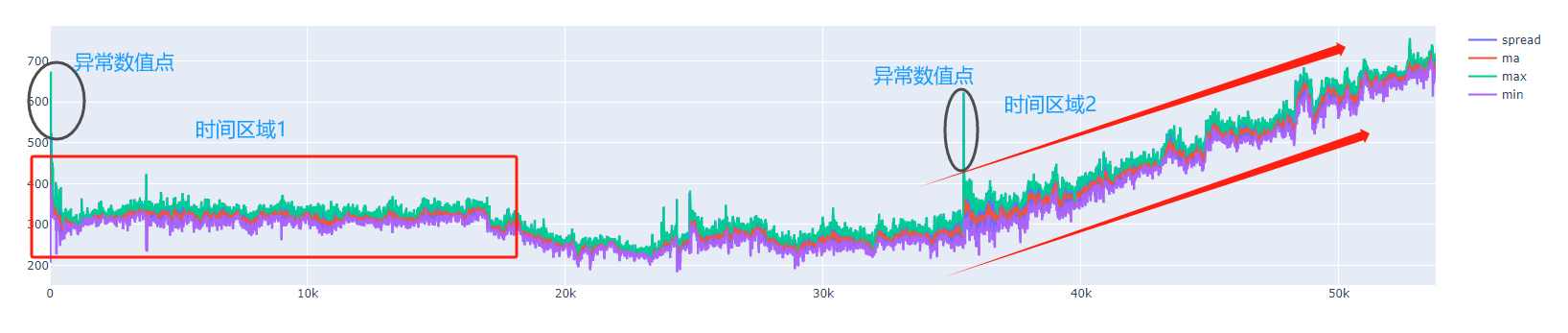
通俗来说：还是以上面比特币的价差图来看，我们期望的价差是时间区域1，整体走势非常平稳，没什么太大振幅，并且不希望出现这种异常数据点，像时间区域2这种上升趋势很明显走势没有一点回归的就被认为是非平稳序列。那有没有一种方式可以将这个走势通过一个数学模型来拟合成类似时间区域1的走势图呢？答案是：可能有！这就需要用到协整性分析了，如果通过这个分析，我们就可以建立VECM（向量误差修正模型）来拟合数据了。
在这里插入图片描述

协整性分析可以帮助我们理解变量之间的因果关系，以及它们之间的长期均衡关系。通过协整性分析，我们可以避免在非平稳序列上进行回归分析时出现伪回归的情况。常用的协整性分析方法包括Engle-Granger方法和Johansen方法。Engle-Granger方法是一种两步法，首先通过单位根检验确定变量是否是非平稳的，然后通过回归分析检验残差是否是平稳的。Johansen方法是一种多步法，它可以同时检验多个变量之间的协整关系。本文就不给大家罗列具体的数学公式了，这些公式在网上也可以查的到，直接给大家上代码。

4. 通过协整性检验

进行协整性测试通常需要以下步骤：

选择需要进行协整性测试的两个时间序列。
对两个时间序列进行单位根检验（Unit Root Test），以确定它们是否平稳。常用的单位根检验方法包括ADF检验（Augmented Dickey-Fuller Test）和KPSS检验（Kwiatkowski-Phillips-Schmidt-Shin Test）等。
如果两个时间序列都不是平稳的，则需要对它们进行差分，直到差分后的序列成为平稳序列。
对差分后的序列进行协整性检验。常用的协整性检验方法包括Johansen协整性检验（Johansen Cointegration Test）和Engle-Granger协整性检验（Engle-Granger Cointegration Test）等。
如果两个时间序列之间存在协整性，则可以使用空间误差校正模型（ECM）对其进行建模和分析。
下面，我们将使用Python的Pandas中的协整性测试方法来进行示范。

import pandas as pd
from statsmodels.tsa.stattools import adfuller, kpss

# 准备数据
data = pd.read_csv('data.csv')  # 从CSV文件中读取数据，确保包含所有相关时间序列
data = data.iloc[:1000,:]	# 选择前1000个数据做拟合适用后续200个数据

result_A_adf = adfuller(data['SA401'])
result_B_adf = adfuller(data['SA405'])
result_A_kpss = kpss(data['SA401'])
result_B_kpss = kpss(data['SA405'])

print('ADF Test - Stock A: p-value =', result_A_adf[1])
print('ADF Test - Stock B: p-value =', result_B_adf[1])
print('KPSS Test - Stock A: p-value =', result_A_kpss[1])
print('KPSS Test - Stock B: p-value =', result_B_kpss[1])

在这里插入图片描述
如果p-value小于0.05，则可以拒绝原假设，即SA401、SA405是平稳的。如果p-value大于等于0.05，则不能拒绝原假设，即SA401、SA405可能是非平稳的。

我们可以看到输出结果中的p-value均小于0.05，因此我们可以认定SA401、SA405均为非平稳序列：

为了使SA401、SA405成为平稳序列，我们需要对它们进行差分。我们可以使用Pandas的diff函数对其进行一阶差分：

df = data[["SA401","SA405"]]
df_diff = df.diff().dropna()

result_diff_A_adf = adfuller(df_diff['SA401'])
result_diff_B_adf = adfuller(df_diff['SA405'])
result_diff_A_kpss = kpss(df_diff['SA401'])
result_diff_B_kpss = kpss(df_diff['SA405'])

print('ADF Test (Diff) - Stock A: p-value =', result_diff_A_adf[1])
print('ADF Test (Diff) - Stock B: p-value =', result_diff_B_adf[1])
print('KPSS Test (Diff) - Stock A: p-value =', result_diff_A_kpss[1])
print('KPSS Test (Diff) - Stock B: p-value =', result_diff_B_kpss[1])

在这里插入图片描述
我们可以看到输出结果中的p-value均小于0.05，因此我们可以认定差分后的SA401、SA405均为平稳序列：

from statsmodels.tsa.stattools import coint

result_coint = coint(df_diff['SA401'], df_diff['SA405'])
print('Cointegration Test - p-value =', result_coint[1])

我们可以得到协整性检验的输出结果如下：

Cointegration Test - p-value = 0.0

由于p-value小于0.05，因此我们可以认为SA401、SA405之间存在协整性。

5. 空间误差校正模型（VECM）

空间误差校正模型（Spatial Error Correction Model, SECM）是一种同时考虑时间和空间依赖性的模型，用于分析具有空间相关性的时间序列数据。SECM可以用来研究时间序列变量之间的协整关系，并纠正由于空间相关性引起的模型偏误。

SECM的基本形式如下：

y_t = α + βx_t + λu_t + ε_t

其中，y_t是因变量的时间序列，x_t是自变量的时间序列，u_t是协整关系的误差项，ε_t是空间相关误差项。α、β和λ是模型的参数。

from statsmodels.tsa.vector_ar.vecm import VECM

# 拟合空间误差校正模型
model = VECM(df_diff, k_ar_diff=1, coint_rank=1)
model_fit = model.fit()

# 获取模型的参数
alpha = model_fit.alpha
beta = model_fit.beta

# 获取误差修正向量（ECV）
ecv = model_fit.resid

# 打印模型参数和误差修正向量
print('Alpha (α):')
print(alpha)
print('Beta (β):')
print(beta)
print('Error Correction Vector (ECV):')
print(ecv)

errors = []
# 根据模型参数和误差修正向量确定交易信号
for i in range(len(df_diff[2:])):
    error = df_diff.iloc[i,0] - alpha[0] - beta[0] * df_diff.iloc[i,0] - beta[1] * df_diff.iloc[i,1] - ecv[i]
    error = error[0]-error[1]
    errors.append(error)
    
import matplotlib.pyplot as plt
plt.plot([i for i in range(len(errors))],errors)

在这里插入图片描述

6. 构建交易策略

统计套利的交易策略一般包括三个信号：当价差偏离均值达到一定标准差幅度时，建仓交易；当其偏离回复到一定程度时平仓获利了结；同时为了防止配对股票原长期均衡关系实际已经破坏的事实，价差将不会回复到均值区间，因此需要进行风险控制，即当偏离超过一定标准差幅度时，止损离场。

对于交易触发信号的确立，有不同的方法。“常用的交易策略如下：当 mspread 的绝对值大于 b 倍标准差时，建仓交易；当 mspread 的绝对值缩小到 a 倍标准差时平仓；当 mspread 的绝对值扩大到 c 倍标准差时强制平仓离场。这里，a<b<c，a，b，c 常用的固定组合值有(0，1，2)，(0，0.75，2)和(1，2，3)等。”除此之外，还有比较激进的交易策略，比如海龟交易策略，到了止损位置，不仅不止损还继续加仓。

# 计算目标仓位
target = 0
target_data = []

for ix, spread in enumerate(errors):
    # 没有仓位
    if not target:
        if spread >= np.std(errors)*1:
            target = -1
        elif spread <= -np.std(errors)*1:
            target = 1
    # 多头仓位
    elif target > 0:
        if spread <= np.mean(errors):
            target = 0
    # 空头仓位
    else:
        if spread >= np.mean(errors):
            target = 0
    # 记录目标仓位
    target_data.append(target)

df = pd.DataFrame()
df["spread"] = errors
df["target"] = target_data
# 计算仓位
df["pos"] = df["target"].shift(1)
# 未扣除手续费和滑点
# 计算盈亏
df["change"] = df["spread"].diff()
df["pnl"] = df["change"] * df["pos"]
df["balance"] = df["pnl"].cumsum()
df["balance"].plot()

在这里插入图片描述

7 总结

对于金融时间序列，往往会出现明显的集群现象。因此这类数据利用时变标准差确定交易时机更合理，它可以更好的挖掘价差序列自回归残差的特性，从而使得统计套利的触发信号更加精准。所以统计套利经常选用GARCH 模型进行具体的统计套利策略研究。具体交易策略可以选择，在价差(Spread)较小(由 GARCH 模型提供合理价差)的情况建仓，在价差(Spread)较大的情况下(由
GARCH 模型提供合理价差) 强制平仓止损，在价差(Spread)回归 0 的时候平仓套利。