1. 题目链接：130. 被围绕的区域

2. 题目描述：

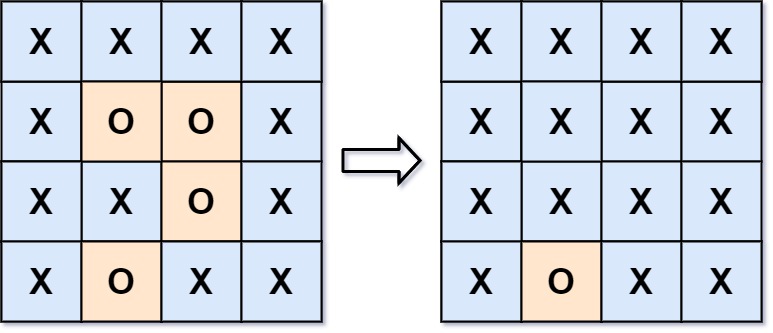
给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 'X' 或 'O'

3. 解法（递归）：

3.1 算法思路：

正难则反

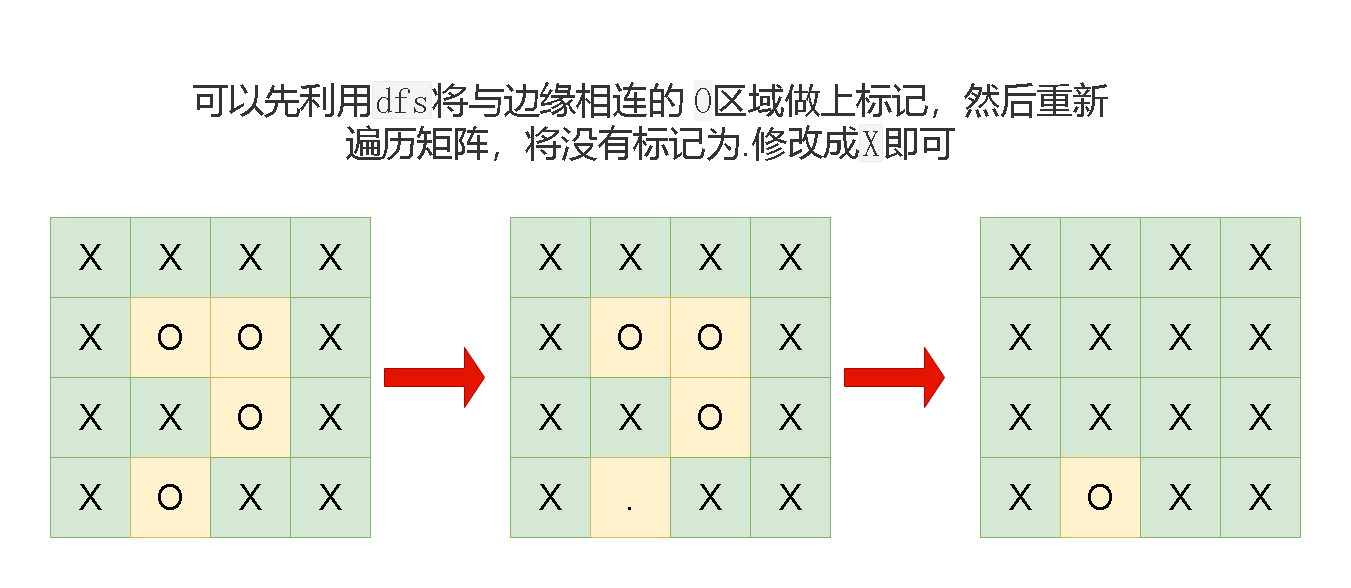
可以先利用dfs将与边缘相连的 0区域做上标记，然后重新遍历矩阵，将没有标记为 .修改成X即可

1. 定义四个方向的横坐标偏移量（dx）和纵坐标偏移量（dy），用于在二维矩阵中进行上下左右相邻元素的访问。
2. 获取矩阵的行数（m）和列数（n）。
3. 遍历第一行和最后一行的元素，如果某个元素为O，则从该点开始进行深度优先搜索，将其标记为已访问。
4. 遍历第一列和最后一列的元素，如果某个元素为O，则从该点开始进行深度优先搜索，将其标记为已访问。
5. 再次遍历整个矩阵，对于每个元素：
   • 如果当前元素为 .，则将其修改为O。
   • 如果当前元素为O，则将其修改为X。
6. 返回修改后的矩阵，其中O表示未被水淹没的岛屿，X表示已被水淹没的岛屿。

3.2 C++算法代码：

class Solution {
    int dx[4] = {1, -1, 0, 0}; // 定义四个方向的横坐标偏移量
    int dy[4] = {0, 0, 1, -1}; // 定义四个方向的纵坐标偏移量
    int m, n; // 定义矩阵的行数和列数

public:
    void solve(vector<vector<char>>& board) {
        m = board.size(), n = board[0].size(); // 获取矩阵的行数和列数
        for (int j = 0; j < n; j++) {
            if (board[0][j] == 'O') dfs(board, 0, j); // 如果第一行的某个元素为'O'，则从该点开始进行深度优先搜索
            if (board[m - 1][j] == 'O') dfs(board, m - 1, j); // 如果最后一行的第一个元素为'O'，则从该点开始进行深度优先搜索
        }
        for (int i = 0; i < m; i++) {
            if (board[i][0] == 'O') dfs(board, i, 0); // 如果第一列的第一个元素为'O'，则从该点开始进行深度优先搜索
            if (board[i][n - 1] == 'O') dfs(board, i, n - 1); // 如果最后一列的第一个元素为'O'，则从该点开始进行深度优先搜索
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == '.') board[i][j] = 'O'; // 如果当前元素为'.'，则将其修改为'O'
                else if (board[i][j] == 'O') board[i][j] = 'X'; // 如果当前元素为'O'，则将其修改为'X'
            }
        }
    }

    void dfs(vector<vector<char>>& board, int i, int j) {
        board[i][j] = '.'; // 将当前元素修改为'.'
        for (int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k]; // 计算下一个元素的坐标
            if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O') {
                dfs(board, x, y); // 如果下一个元素为'O'，则继续进行深度优先搜索
            }
        }
    }
};