微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

利用香农公式对连续信道的信道容量计算
根据香农公式,高斯白噪声背景下的连续信道的容量为
Ct=B×log2[(1+(S/N))]=B×log2[(1+(S/(n0×B)))]
B为信道带宽,单位Hz
S为信号功率,单位W
n0为噪声单边功率谱密度,单位为(W/Hz)
N=n0×B为噪声功率,单位W
S/N为信噪比,单位dB
注意:当信道容量C≥信源的信息速率Rb时,即C≥Rb,则理论上可实现无误差传输。
香农公式的重要结论
①连续信道容量C受带宽B和信噪比S/N
②提高信噪比S/N,可增大信道容量C
③若n0→0,则C→∞,说明无扰信道的信道容量为无穷大
④若S→∞,则C→∞,说明当信号功率不受限时,信道容量为无穷大
⑤当B→∞,则C→1.44(S/n0)
⑥若信源的信息速率Rb≤C,则理论上可实现无误差传输
信噪比SNR用分贝(dB)表示,信噪比的计算公式
SNR=10×lg(S/N)
例题一:
彩色电视图像信号,每秒25帧,每帧有1024 × 768个像素,每像素三个色彩强度分别量化成64个量化级,该信号经压缩比为8:1的图像压缩编码器。另有128kb/s×2的立体声信号。求:
①该数字电视信号的总速率;
②若信道信噪比为30dB,传输该数字信号所需的频带宽度;
③若信道带宽为8MHz,所需要的信噪比;
④在(3)的条件下,若采用MQAM调制传输该信号,需要的最小进制数M。
解析:
①每个像素的信息量:I(像素)
=-log2[(1/64)×(1/64)×(1/64)]
=18(bit)
压缩后每秒图像的信息量:I
=1/8×1024×768×18
=1769472(bit)
图像信号的速率:Rb
=25×I=44236800(bit/s)
数字电视信号的总速率(图像信号和立体声信号总和):R
=44236800+128000×2(bit/s)
=44492800(bit/s)
②由香农公式可得
Ct=B×log2[(1+(S/N))]
其中C≥R,S/N=30dB
B≥4463910Hz
③由香农公式可得
Ct=B×log2[(1+(S/N))]
B=8M,Ct=Rb
信噪比S/N=46.23
SNR=10×lg(S/N)≈16.6dB
④MQAM调制为M进制数
Rb=RB×log2(M)
RB≤8000000
Rb/(log2(M))≤8000000
M≥47.23
M最小为64进制
例题二:
某电视信号每帧有1024×540个像素,每个像素有3个色彩强度和1个亮度参数,它们各有8级,每秒有25帧。信道信噪比为30dB。试求:
①电视信号的信息速率;
②传输该信号所需要的带宽;
③若信道带宽限制在8MHz,所需的信噪比。
解析:
①每个像素的信息量:I(像素)
=-log2[(1/8)×(1/8)×(1/8)×(1/8)]
=12(bit)
每秒图像的信息量:I
=1024×540×12
=6635520(bit)
电视信号的信息速率:Rb
=25×I=165888000(bit/s)
②由香农公式可得
Ct=B×log2[(1+(S/N))]
其中C≥R
SNR=10×lg(S/N)=30dB
S/N=10^3
B≥16643346Hz
③由香农公式可得
Ct=B×log2[(1+(S/N))]
B=8M,Ct=Rb
信噪比S/N=1746456
SNR=10×lg(S/N)≈62dB
例题三:
已知黑白电视图像信号每帧有32万个像素,每个像素有16个电平,各电平独立地以等概率出现,图像每秒发送25帧。若接收信噪比为40dB。
①试求所需传输带宽。
②若带宽加倍,则需要的信噪比是多少dB。
解析:
①每个像素的信息量:I(像素)
=-log2[(1/16)×(1/16)]
=8(bit)
每秒图像的信息量:I
=320000×8
=2560000(bit)
电视信号的信息速率:Rb
=25×I=64000000(bit/s)
由香农公式可得
Ct=B×log2[(1+(S/N))]
其中C≥R,SNR=40dB
SNR=10×lg(S/N)
S/N=10^4
B≥4816428Hz
②B带宽加倍
B×log2[(1+10^4)]=2×B×log2[(1+(S/N))]
S/N=99
SNR=10×lg(S/N)
SNR≈20dB
通信原理板块——利用香农公式对连续信道的信道容量计算
news2026/2/15 8:24:57
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1214478.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
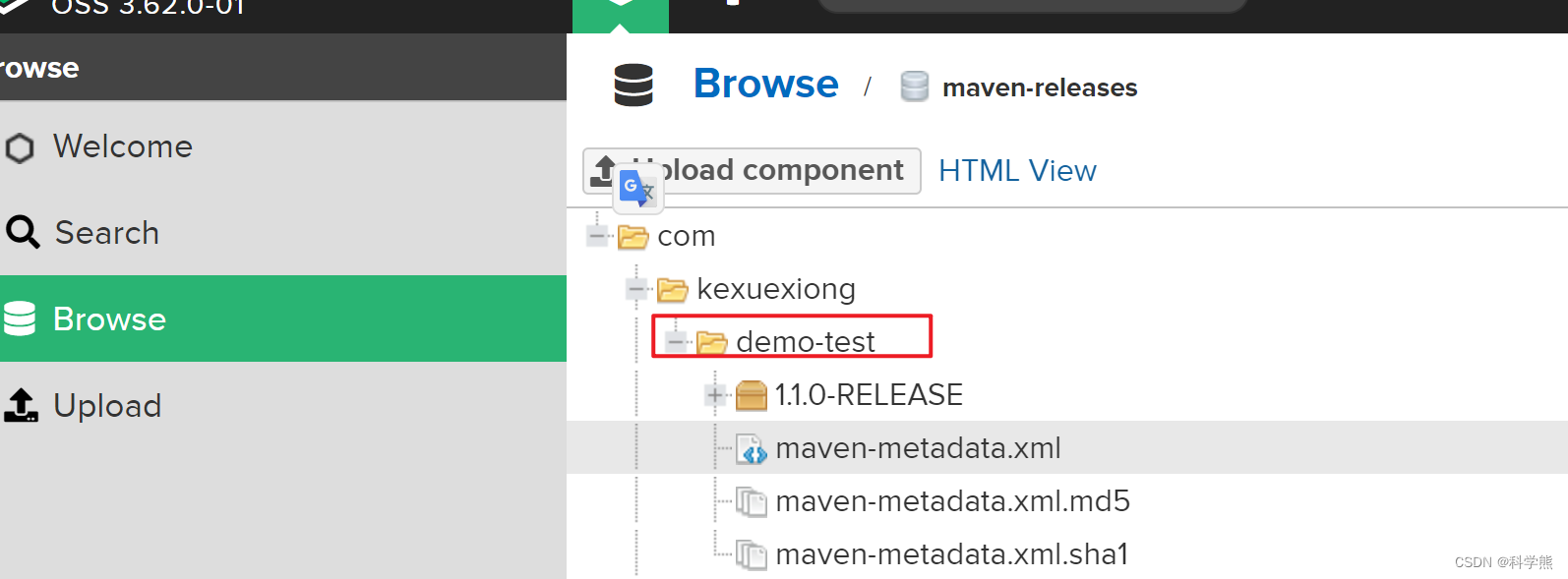
通过maven命令手动上传jar私服Nexus
Nexus3在界面上传组件时报: Ext.JSON.decode(): Youre trying to decode an invalid JSON String: 查找了很多资料,都没有解决。有哪位大佬知道的评论告诉一下,万分感谢。
于是换成maven命令上传:
mvn deploy:deploy-file -Dgr…
基于springboot实现一起来约苗管理系统项目【项目源码】计算机毕业设计
基于springboot实现一起来约苗管理系统演示 Java技术
Java是由Sun公司推出的一门跨平台的面向对象的程序设计语言。因为Java 技术具有卓越的通用性、高效性、健壮的安全性和平台移植性的特点,而且Java是开源的,拥有全世界最大的开发者专业社群ÿ…
如何快速找到华为手机中下载的文档
手机的目录设置比较繁杂,尤其是查找刚刚下载的文件,有时候需要捣鼓半天,如何快速找到这些文件呢?以下提供了几种方法:
方法一:
文件管理-》搜索文档 方法二:
文件管理-》最近 方法三…
如何使用Omniverse Kit开发元宇宙
最近我研究了一些潜在的元宇宙开发平台。尽管Facebook上个月引发了关于元宇宙的最新一轮炒作,但另一家公司英伟达(Nvidia)在开发实际元宇宙平台方面走得更远。Nvidia的Omniverse自2019年以来一直在运行,因此在今天的帖子中&#x…
Python武器库开发-flask篇之模板渲染(二十四)
flask篇之模板渲染(二十四)
Flask 中的模板是一种将数据和 HTML 代码组合在一起的方式,使得我们可以生成动态的 HTML 页面。使用模板可以使我们的代码更加简洁、易于维护和复用。在真实的环境中,我们往往接触到的是由 html、CSS和JavaScript所做的网页&…
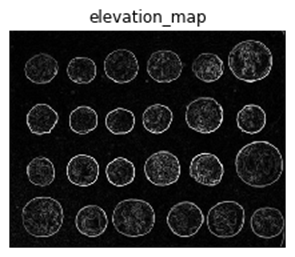
使用 Python 的基于边缘和基于区域的分割
引言
在本文中,我们将重点讨论基于边缘和基于区域的分割技术。在讨论细节之前,我们需要了解细分它们分别是什么以及它们是如何工作的。 分割
图像分割是一种将数字图像分割成各种图像对象的技术。
区域中的每个像素(图像对象)在某些属性(如颜色、亮度…
【新版Bing】集成chatGpt4的搜索引擎
具体步骤 打开Chrome浏览器,进入无痕模式。 访问bing.com/new;(需要kexueshangwang,评论区有具体方法) 注册账号或使用老帐号登录(我是直接用的老帐号) 注册界面 登录成功 点击在Microsoft Edge中…
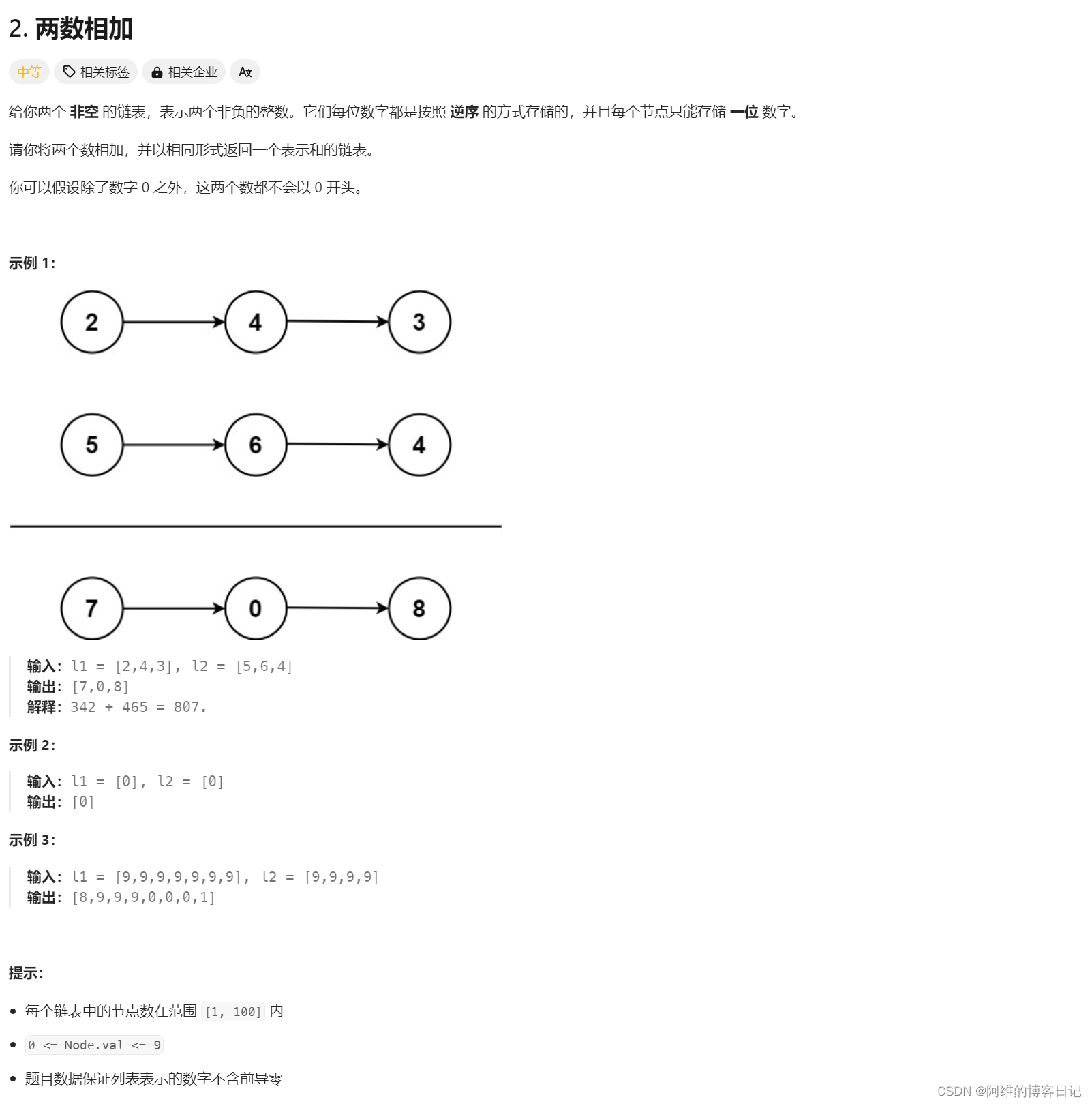
LeetCode2-两数相加
大佬解法
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val x; }* }*/
class Solution {public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode pre new ListNode(0);ListNo…
YOLOv8原创改进:最新原创WIoU_NMS改进点,改进有效可以直接当做自己的原创改进点来写,提升网络模型性能精度
💡该教程为属于《芒果书》📚系列,包含大量的原创首发改进方式, 所有文章都是全网首发原创改进内容🚀 💡本篇文章为YOLOv8独家原创改进:独家首发最新原创WIoU_NMS改进点,改进有效可以直接当做自己的原创改进点来写,提升网络模型性能精度。
💡对自己数据集改进有效…
langchain 之 Tools 多案例使用(一)
原文:langchain 之 Tools 多案例使用(一) - 简书
ATTENTION:
如果采用 openai 的接口,需要走代理,本文采用 proxychains 进行设置。开启 debug 模式后,能看到更多的输出信息。
import langchain
langcha…
黑马程序员微服务 分布式搜索引擎3
分布式搜索引擎03
0.学习目标
1.数据聚合
**聚合(aggregations)**可以让我们极其方便的实现对数据的统计、分析、运算。例如:
什么品牌的手机最受欢迎?这些手机的平均价格、最高价格、最低价格?这些手机每月的销售…
CentOS to 浪潮信息 KeyarchOS 迁移体验与优化建议
浪潮信息KeyarchOS简介
KeyarchOS即云峦操作系统(简称KOS), 是浪潮信息研发的一款面向政企、金融等企业级用户的 Linux 服务器操作系统。它基于Linux内核、龙蜥等开源技术,支持x86、ARM 等主流架构处理器,其稳定性、安全性、兼容性和性能等核心能力均已…
京东账单导出的手工操作
文章目录 京东账单导出的手工操作概述笔记备注备注END 京东账单导出的手工操作
概述
在京东网页版找不到账单导出的操作. 在手机京东中可以导出账单. 当前京东APP的导出实现有点bug, 在输入验证码后, 发送邮件. 可是显示验证码失败, 但是已经发了邮件. 可能是因为发送成功提示…
requests库进行HTTP请求时,有时需要传递cookies参数
在使用requests库进行HTTP请求时,有时需要传递cookies参数。但是,requests库的cookies参数只能接受CookieJar对象,而不能接受字典等其他类型的cookies。
在requests库中增加对字典类型的cookies支持,使其能够接受字典类型的cooki…
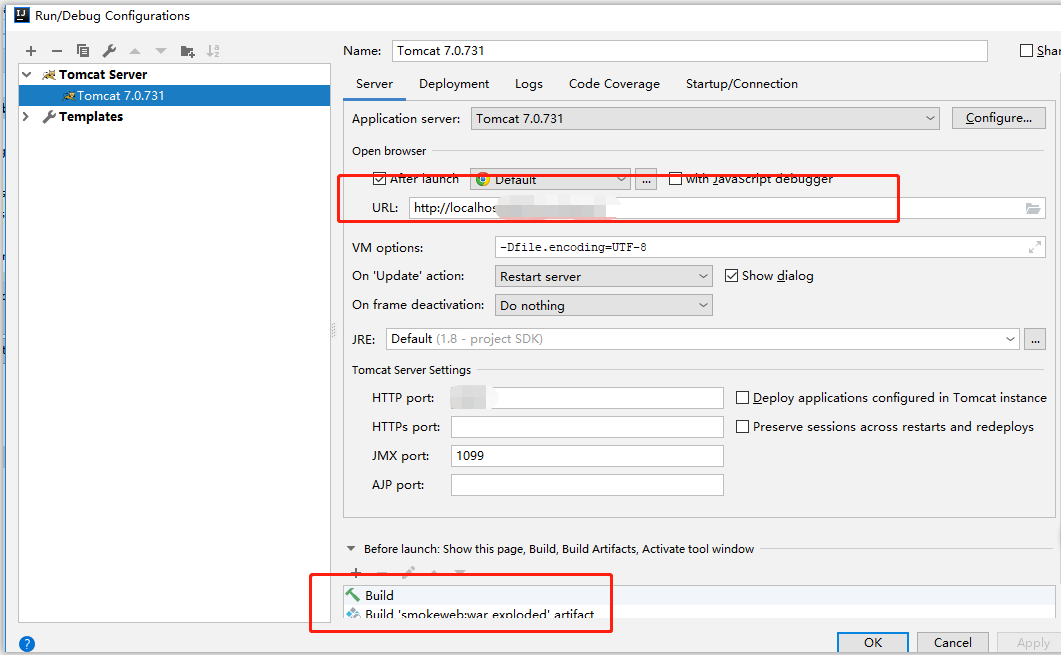
IntelliJ IDEA启动一个普通的java web项目的配置
原创/朱季谦 这是我很久以前刚开始用IntelliJ IDEA时记录的笔记,应该是五年前的一篇笔记了。正好赶上最近离职了,可以有比较多的时间把以前的记录整理一下,可以让刚接触到IntelliJ IDEA的童鞋学习如何在IntelliJ IDEA引入一个单机版的jar形式…
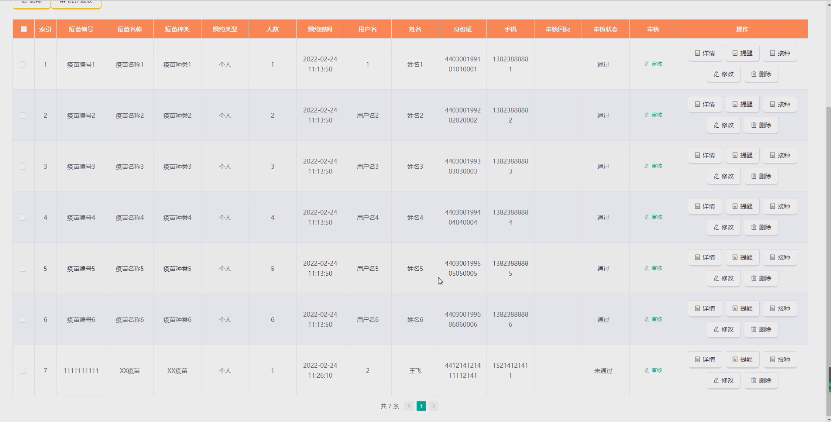
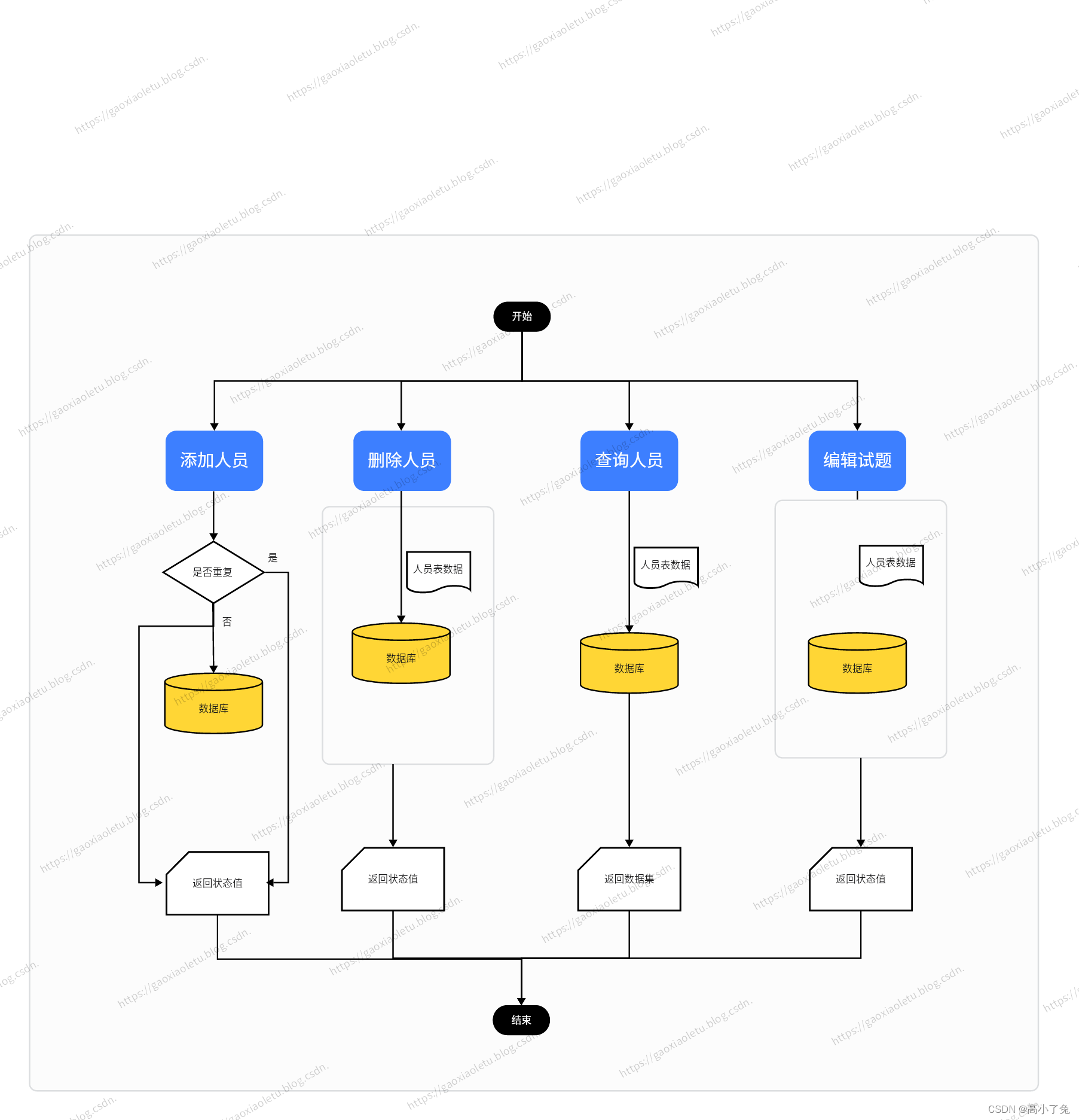
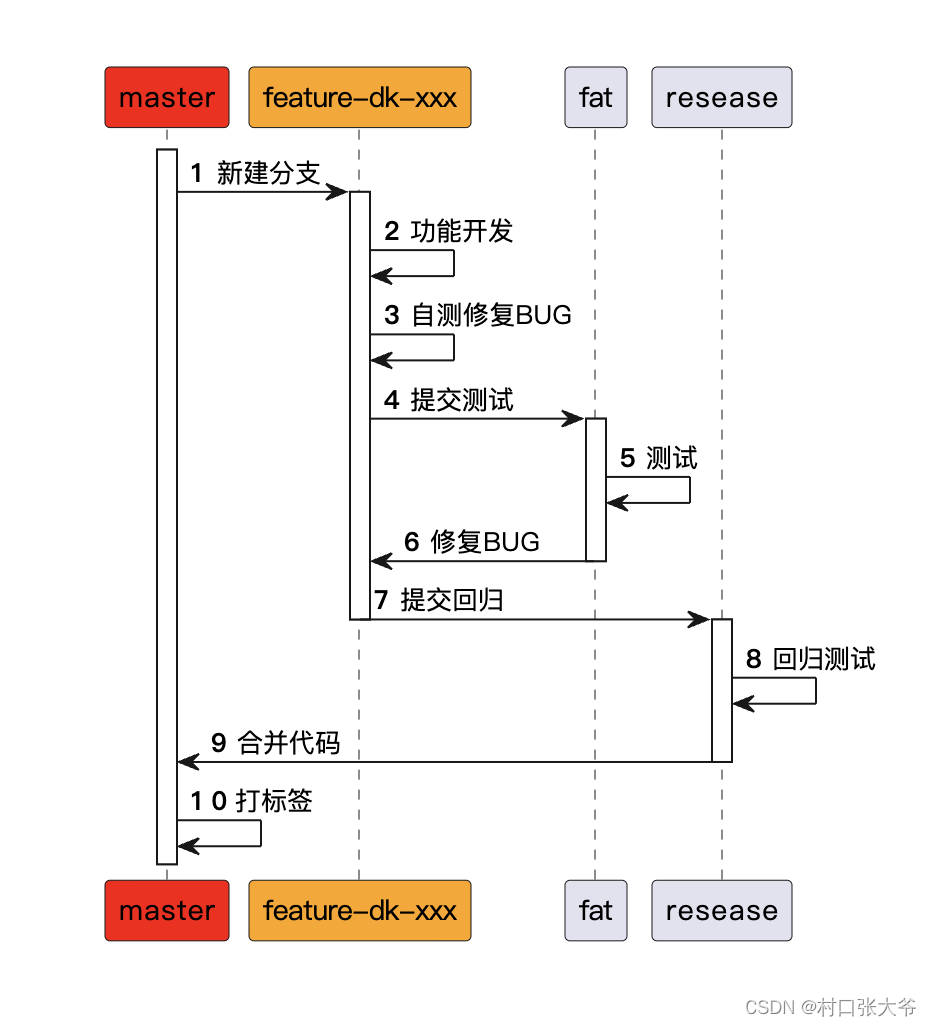
第三篇 《随机点名答题系统》——人员管理详解(类抽奖系统、在线答题系统、线上答题系统、在线点名系统、线上点名系统、在线考试系统、线上考试系统)
目录
1.功能需求
2.数据库设计 3.流程设计
4.关键代码
4.1.人员分组
4.1.1数据请求示意图
4.1.2添加组别(login.php)数据请求代码
4.1.3编辑组别(login.php)数据请求代码
4.1.4加入分组(login.php)…
安装包管理工具-Yarn
一、介绍与安装
1.1 介绍
Yarn是一款功能包管理工具,与npm(npm:Node.js 的包管理器 npm,是目前最流行的Node.js 的包管理器。)类似。有着FAST(快速的), RELIABLE( RELIABLE 可信赖的), AND SECURE DEPENDENCY MANAGEMENT(安全依赖关系管理)的特点。 Yarn官网
1.2…
【2016年数据结构真题】
已知由n(M>2)个正整数构成的集合A{a<k<n},将其划分为两个不相交的子集A1 和A2,元素个数分别是n1和n2,A1和A2中的元素之和分别为S1和S2。设计一个尽可能高效的划分算法,满足|n1-n2|最小且|s1-s2|最大。要求…