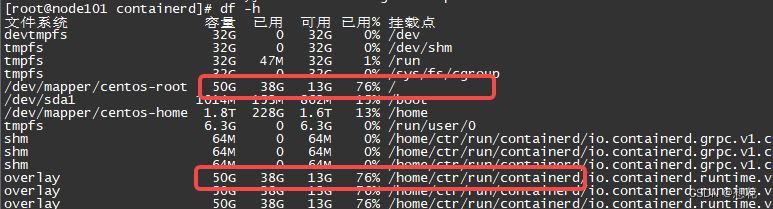
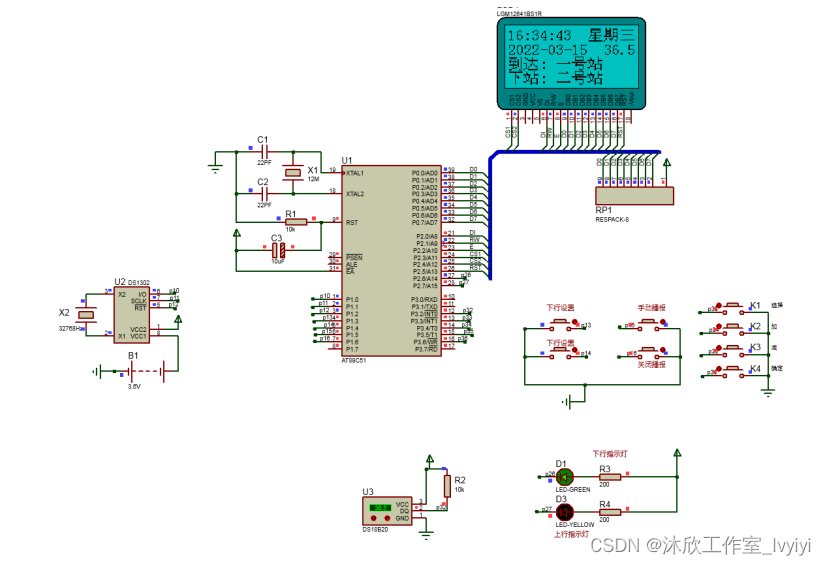
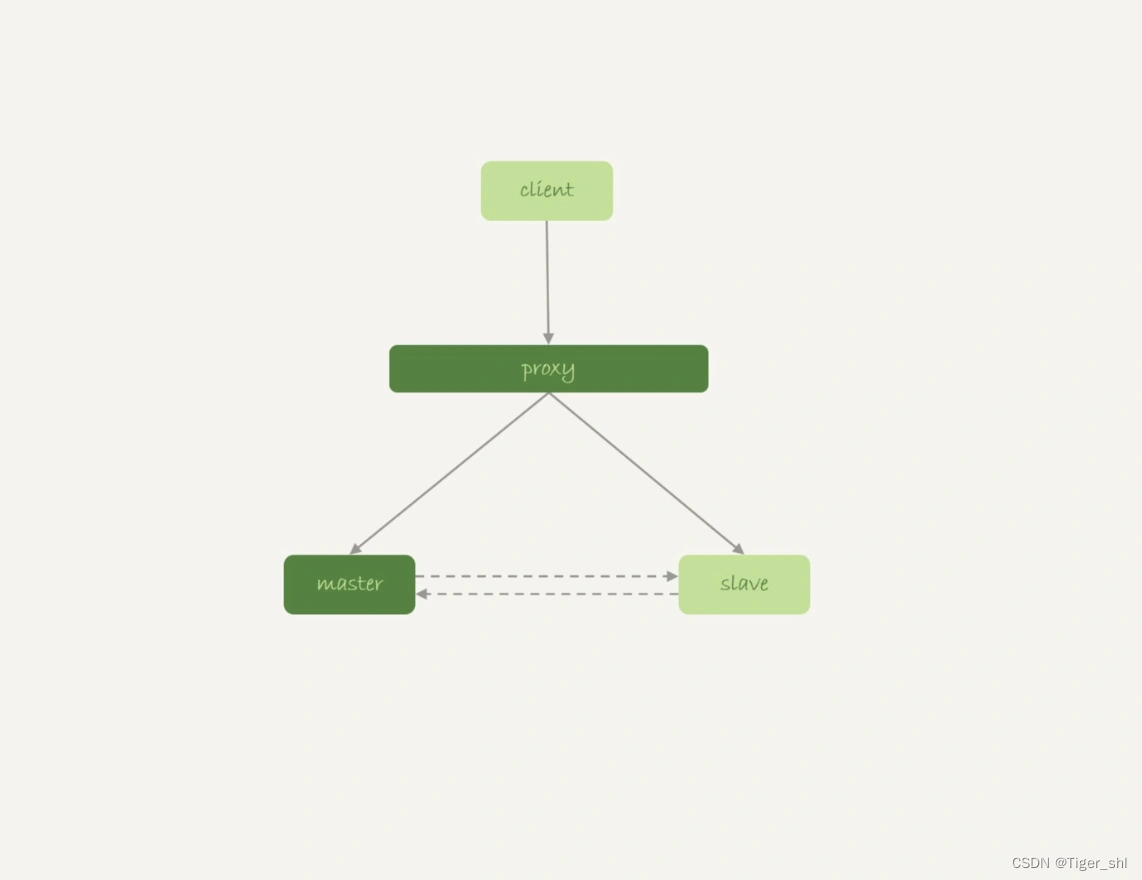
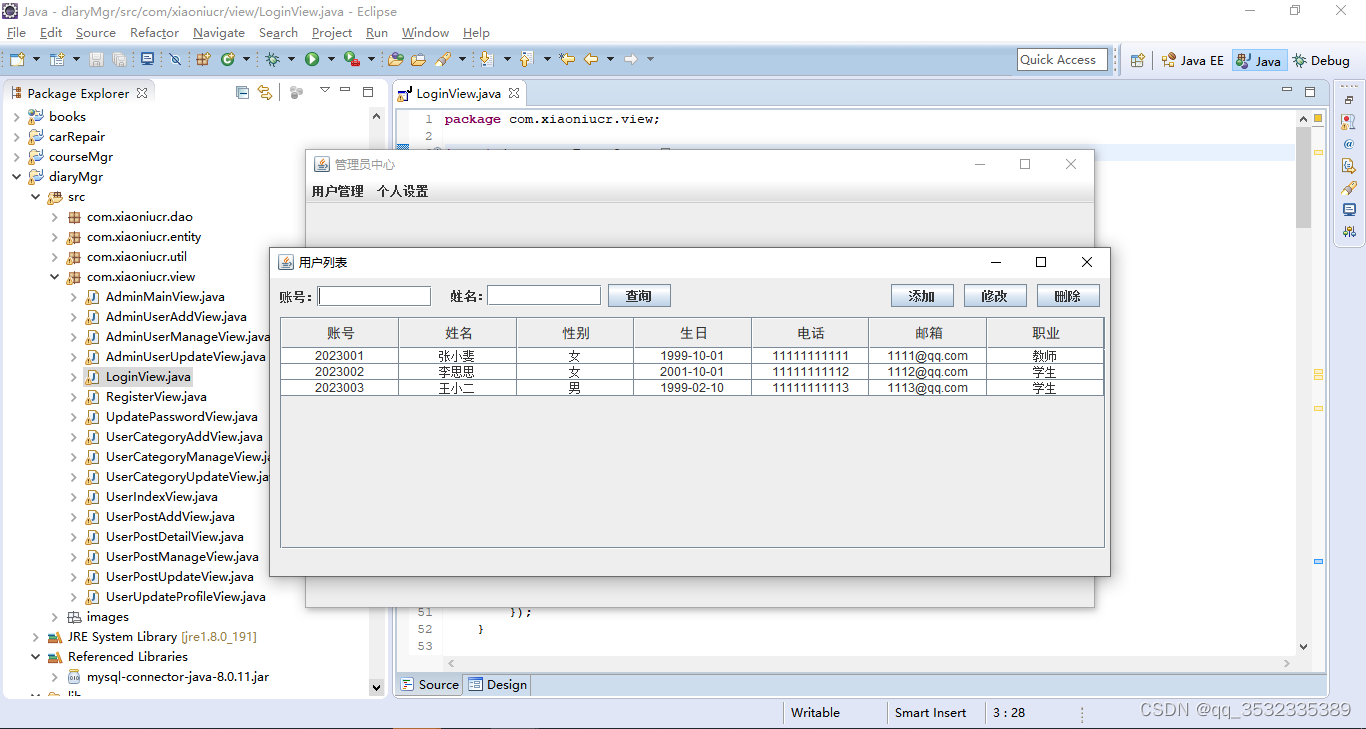
读这篇15年CVPR的文章🤣🤣🤣🤣🤣
@inproceedings{liu2015sparse,
title={Sparse convolutional neural networks},
author={Liu, Baoyuan and Wang, Min and Foroosh, Hassan and Tappen, Marshall and Pensky, Marianna},
booktitle={Proceedings of the IEEE conference on computer vision and pattern recognition},
pages={806--814},
year={2015}
}
原文有这么一句话:
Decompose K and R using Principal Component Analysis (PCA), with P, Qi the principal components.
就,PCA降维我知道,这个还能做矩阵分解? 算了,顺便回忆下PCA的流程,为春招做准备(卑微组加一分😂😂😂
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1942)
本意是想绘制一个椭圆
point_num = 13000
x_y = np.random.randn(point_num, 2) * 5
bool_idx = (x_y*x_y / np.array([64, 1])).sum(1) < 1
x_y = x_y[bool_idx]
plt.scatter(x_y[:, 0], x_y[:, 1])
plt.show()

如果此时给这些点组成的矩阵降维的话,由于样本在水平方向的分布比竖直方向的分布更加散得开,所以降成1维之后,留下的是坐标x,也就是这个图的样子:
# 由于点太多,会使这个图显示一条线段,于是此处 point_num = 130
plt.scatter(x_y[:, 0], y=np.zeros_like(x_y[:, 0]))

(记住这个图,后边有用🚀🚀🚀)
给它逆时针旋转30度
# 将椭圆逆时针旋转 30 度
theta = np.pi / 6
rotate = [
[ np.cos(theta), np.sin(theta)],
[-np.sin(theta), np.cos(theta)],
]
rotate = np.array(rotate)
x_y_new = np.matmul(x_y, rotate)
plt.figure()
plt.scatter(x_y_new[:, 0], x_y_new[:, 1])
plt.show()

算一下协方差矩阵
Σ = 1 n − 1 ( ( X − x ˉ ) T ( X − x ˉ ) ) \Sigma = \frac{1}{n-1} \left ( \left ( X - \bar{x} \right )^T \left ( X - \bar{x} \right ) \right ) Σ=n−11((X−xˉ)T(X−xˉ))
x_bar = x_y_new.mean(axis=0)
cov_mat = np.matmul((x_y_new - x_bar).T, x_y_new - x_bar)
cov_mat
array([[13718.36010864, 7691.12792157],
[ 7691.12792157, 4860.68354368]])
# 计算特征值和特征向量
val, vec = np.linalg.eig(cov_mat)
val, vec # vec 是两个列向量
(array([18164.65885261, 414.38479971]),
array([[ 0.8657414 , -0.50049159],
[ 0.50049159, 0.8657414 ]]))
由于原特征只有两维,所以我们直接取第一个特征值比较大的特征向量,进行降维操作
data_low = np.matmul(x_y_new, vec[:, 0][:, None])
plt.scatter(x=data_low, y=np.zeros_like(data_low))

降维之后的图,和前面那个图一样
其实可以看下,PCA找的的特征向量和之前的旋转角度有啥关系:
# plt.scatter(x_y_new[:, 0], x_y_new[:, 1])
# 由于数据量有限, 所以PCA找到的旋转角度有一定误差
plt.arrow(0, 0, vec[:, 0][0], vec[:, 0][1], length_includes_head=False, head_width=0.05, fc='b', ec='k')
plt.arrow(0, 0, np.cos(theta), np.sin(theta), length_includes_head=False, head_width=0.05, fc='b', ec='k')
plt.show()
# matplotlib 箭头绘制参考自:
# https://zhuanlan.zhihu.com/p/452828891
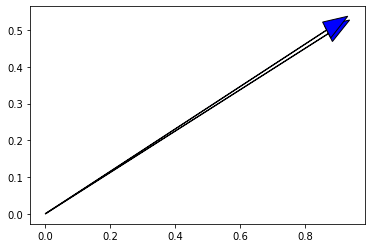
可以看到 point_num = 130 时,二者差一丢丢重合
当 point_num = 130000 时,二者基本重合
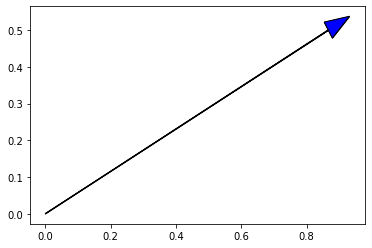
感觉原文可能是想说,奇异值分解(SVD)?
对中心化后的样本矩阵做SVD的过程就是PCA
有参考自:https://blog.csdn.net/qq_29153321/article/details/105361428