置信度,置信区间
给定一个置信度,就可以算出一个置信区间。
如果给的置信度越大,那么阿尔法就越小
给的置信度越小,那么α就越大,那么
考虑精确性,希望区间长度尽可能小,所以是取正态的中间的对称位置
置信度越高,则精度越低,反之,精度越高则置信度越低
置信水平描述真实值落在置信区间中的概率
当你要提高置信水平(即真实值落在置信区间中的概率)的时候,相应的将要付出的代价就是拉长置信区间,也就是区间半径的增大。
那么很显然的,如果你想让一个区间保持完美的,100%的可靠度,在已有的条件下,我只能将区间半径拉长到∞。也就是置信区间为R。
那么显然这个参数估计就失去了意义,自然不存在可靠性。
另外的,置信水平和显著性水平是负相关的,并且置信水平与显著性水平的和为1

错误理解:上图浅色的虚的竖直线代表样本参数真值,横的两端有端点的代表95%置信度的置信区间,100条竖直线里有95条左右落入这个区间内。
这是非常错误的理解,样本与总体的关系没有思考清楚。置信区间是估测总体参数的真值,这个值只有一个,且不会变动。
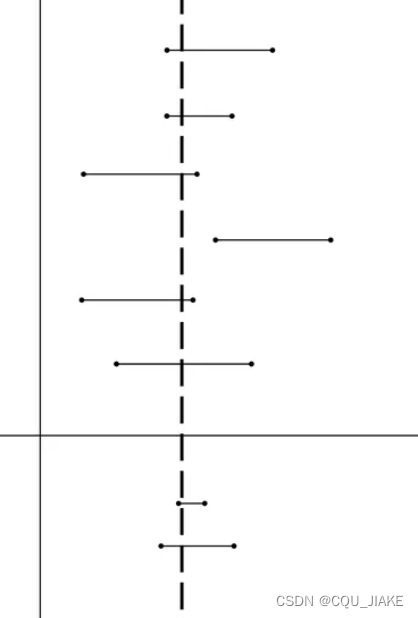
样本数目不变的情况下,做一百次试验,有95个置信区间包含了总体真值。置信度为95%
其中大虚线表示总体参数真值,是我们所不知道的想要估计的值。正因为在100个置信区间里有95个置信区间包括了真实值,所以当我们只做了一次置信区间时,我们也认为这个区间是可信的,是包含了总体参数真实值的。
置信区间是变的,是不固定的,课本上让求的那个置信区间,只是某种条件下的置信区间(可能是区间长度最短的置信区间),但实际上只要这个区间上的点占总点的置信度,就是一个置信区间
上分位点
就是右侧占α,类似相同的概念就是分布函数,只不过分布函数是左侧的总体的
对于对称的分布,正态,t分布,1-α和α是对称的,即分布在对称轴左右
对于不对称的分布,F分布,是一个倒数关系
对于卡方分布,相对关系很复杂,要查两次表
上分位点出来的是x轴上的一个值,由于是右侧占α,所以α越小,这个值越大,反之则越小
即右侧占的越多,那么分位点越靠前,右侧占的越少,分位点越靠后。
正态分布用分布函数描述,即左侧占比;t分布,卡方分布,F分布都是右侧占比。t,卡方
正态分布也可以用分位点去描述,为u。
不过分位点出来的是坐标轴上的数,分布函数出来的是左侧占1的比例大小,相当于一个反函数的关系。
假设检验
假设方式
假设方式有是不是,与偏大还是偏小,即单尾检测与双尾检测
单尾检测就是判断是否高于或是否低于,
对于均值的单尾检测
如果考虑样本低于总体,那么原假设就是大于等于总体,新假设H1是低于总体
因为左加右减,所以当分布发生变化,均值越大,减的数越大,左加右减,相当于在原基础上又减了数,所以就越会在标准分布中向右偏;均值越小,减的数越小,在原来基础上加了数,就会越往左偏。
也就是标准分布中,也能体现出一定的原来均值的位置,先根据相应的均值定义出一个标准的分布,然后向右偏的,都是均值偏大的样本数据;向左偏的,都是均值偏小的样本数据。所以极左极右发生时,就意味着当前定义的均值所产生的标准分布失去了参考意义,即数据分布发生了变化,在单尾检测中,如果偏小,就是分布在左侧的1-α分位点;如果偏大,就是分布在右侧的α分位点
对于双尾检测
就不考虑到底是偏大还是偏小,只是考虑到底还是不是原分布,在单尾检测中,只检测一端,所以允许分布偏离原分布,向相反方向偏离都可以,但就是不允许向指定的检测方向偏移,所以对某个方向的检测更加严格;
而双尾检测就不关心这个,它只关心到底还是不是原分布,所以极左与极右都不允许发生,相应的显著性水平也就不止分散在一端,而是两端各分一半,这也就意味着相比单尾检测的一端不那么严格,因为单尾检测是全部的α都分布在一侧,而这里只分布着一半。、
所以双尾检测的重点就放在了,到底”是不是“的问题上
即两种假设方式分别为
![]()
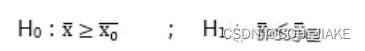
与
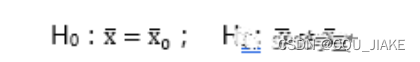
即单尾检验用不等式,双尾检验用等式
单变量检验
单变量检测中,重点在于均值与方差是否等于某个值,对于均值而言,意义比较明显,就是和以往相比检测是否合格,是否认为是不是某个值;对于方差的单变量检验,意义不那么明显,因为方差难以直观的用数字去感知与衡量,基于比较才有直观的含义,即波动是偏大还是偏小,而由于是单变量,所以比较的值一般就是基于之前的历史值或经验值。
均值检验采用正态与t,方差采用卡方。
对均值进行检验,就是正态分布;根据方差是否已知,采用不同的分布,但都是正态型的。
如果方差已知,取几个样就有多少复杂度;如果未知,就要用计算出的方差,自由度就要失去一个,退化为t分布
对方差进行检验,就是要卡方分布;
如果均值已知,那就是取样个数的自由度;不然,就要失去一个自由度。
在假设过程中,所使用的方差都是假设的那个值。不过就是均值已知时就用均值,均值未知时就用计算出的均方差;
用了均方差,就会丢一个自由度。
在均值检验中,均方差用于弥补未知方差的信息;在方差检验中,均方差用于弥补未知均值的信息。方式都是乘(n-1)后,分子分母消除掉的标准差,凑成的那个自由度为n-1的卡方分布实现。
在均值检验中,用于形成n-1自由度的卡方分布,从而形成n-1的t分布,进行检验
在方差检验中,就是直接形成n-1自由度的卡方分布,进行检验
在均方差中,用的就不是总体分布的均值,而是样本的均值,所以自由度才会-1,所以在方差均值未知时,就可以规避掉未知的总体均值信息;在均值检验中,方差未知时,如果方差已知,直接构造标准正态就可以进行检验,因为检验均值,相对于假设均值已知,总体方差又已知,所以可以直接求解;如果方差未知,就不能直接转为标准正态分布。而t分布,由于是标准正态分布除以卡方分布,所以在方差未知时可以规避掉未知的方差信息,从而构造出最大可能利用已知信息的t分布
方差检验,就是假设方差是已知的;均值检验,就是假设均值是已知的
对于标准正态分布,就是总体的方差,均值都已知。
对于T分布,可以在总体方差未知时发挥作用
对于卡方分布,若为n自由度,则总体的方差,均值都已知
若为n-1自由度,那么总体均值未知,通过除以已知的方差,将均方差转化为自由度为n-1的卡方分布
双变量
双变量的检测,重点在于检测两个变量的均值是不是相等,方差是不是相等,重点在于是否相等上,而不是是多少的问题上
所以在假设中,假设都是等于还是不等于。所以在均值检测当中,要构造第一个的均值减去第二个的均值的统计量;在方差检验中,是构造作比的F分布
均值检验中,
用正态分布与t分布
在这一部分中,有一特殊情况就是n1=n2,即两个体系中取的样本数量相等,那么就可以化为配对,一组一组,即合并成新的统计量,如果方差已知,就是正态,否则,就用t统计量。即所谓配对问题。
一般是取样数量不相等,即一个取得多,一个取得少,那就是整成各自的均值与方差进行计算
方差检验中,
用F分布
均值已知时,那么两个变量各自可以构造出各自自由度的卡方分布,相比,就是F(m,n)的F分布
均值未知时,就需要通过均方差,构造出各自自由度-1的卡方分布,相比,即m-1,n-1的F分布
F分布只能用来检测两个变量的方差是不是相等,即数据波动程度是否一致,而判断不出来方差的具体数值。在F分布中,两个卡方分布相比,都把方差消掉了,而这个消掉过程,就是基于他们方差相等,如果不相等就不能消掉,所以如果不符合F分布的大概率事件,就不能认为他们方差相等。
两类错误
显著性水平的含义就是原假设成立时,放弃原假设,取H1的概率,即第一类错误,弃真错误的概率;
另一种错误是说,原假设错误,但是选择了原假设,即取为假设。
错误就是错误,对于每种具体情况而言,第一类错误与第二类错误所标注的实际意义的情况不会同时发生,但当”弃真“时,就意味着”取伪“
他们的本质区别就在于,原假设是不是正确的假设,如果原假设正确,那么判断错误时,就是放弃原假设H0,即弃真错误;如果原假设错误,那么判断错误时,就是选择原假设,即取伪错误
所以,第一类第二类错误只是对同一种错误的不同描述方式,他们的概率判断没有意义,因为不可能针对同一种假设同时发生,因为每次只会发生一种错误,在唯一确定原假设的情况下,第一第二类错误并不是对错误整体集合的一个划分,而是对错误集合的命名方式,依据原假设的不同而发生变化。
第一类错误的概率计算,就是原假设为真,但是弃真,即统计量最终落在了拒绝域里;
第二类错误的概率计算,就是原假设为假,但是取伪,即统计量最终没落在拒绝域里。
此外,需要注意,标准的分布是基于正确的假设上的,错误的假设不被认为构成标准分布,即对应的统计量,实际上在错误的假设上并不服从标准分布,而只有在正确的参数下才是标准的分布
故,在第一类错误,弃真中,标准的定义是H0,即原假设;在第二类错误,取伪中,标准的定义是备选H1,即备选假设,原假设不被认为构成标准分布。
通过两类错误增大样本容量
一般思路是控制第一类错误的概率,依据第二类错误的概率,来确定样本容量的要求
即在原假设的基础上,可以知道某个原始量的分布范围,在接受的情况下,即接受原假设会对应某个量的一个区间,此时假设原假设是不对的,再假设实际参数是某个数,希望第二类错误的概率不要超过某个期望的值,也就是说,此时的分布与分布公式就变化了,但依据原来的错误假设,已经算出来了一个分界点,即取伪区间,那么在这个正确的分布下,其在标准分布里,占据的比例不应该超过所期望的值,所以就对应可求出所需的样本量的要求
因为取伪,就是因为原假设是错误的,但是就是发生了,取了它
实际上不是的话,那么它发生的概率应该是小的,第二类错误就是所谓瞎猫碰上死耗子。
?为什么是要在原假设里求出接受域的范围,而不是在正确的假设里?
两个参数,要先取伪,首先是因为不知道它是“伪”,其次是要取它,即在不知情的情况下,不发生“第一类错误”,这里就用到了第一类错误的参数,α,要让统计量落在它所界定的接受域内,才会接受原假设,才会取伪;第二个参数,发生的概率,就是在一种极端假设上,对于原假设的怀疑,即如果原假设不是真的,又有多大把握避免这一错误
检测方式
在置信区间中,一般是左端占α/2,右端占α/2,中间占1-α。即无论那种分布,样本总是围绕在均值的左右,极左与极右都是极端的小概率事件。假设检验就是为了检测这样的小概率事件是否发生。
显著性水平越大,左右不被允许的区间越大,也就是弃真错误率越大,即原假设正确时,判断错误的概率,也就是对样本的分布更加苛刻,越要求它紧紧分布在均值两侧;反之,则越宽松。
步骤就是先依据已有的信息,选定合适的统计量与分布方式,那么就可以化为相应标准统计量的分布,注意,是标准统计量的分布,这个统计量综合了一切的信息(并非单一样本,某个样本的信息,而是样本总体的一个信息,所以不存在多个这样的统计量,每次取样都只会综合出一个这样的统计量),应该满足相应的条件,即最终应该落在标准分布均值左右的两侧,即置信区间内。
而依据显著性水平,就可以得到左右两侧小概率事件的分布的概率,也可以说是分界线,也就是要求综合了一切信息的统计量应当在拒绝域之外,置信区间内,这要才符合大概率,大数定律,否则就是小概率事件的发生(即在当下这个假设下,由多次取样出的一个样本总体情况在当下假设中出现了分布异常,即发生概率很小的小概率事件)
显著性水平用来确定拒绝域;
已知条件用来确定统计量是什么,选取什么样的统计量进行检验;
具体数值与查表用来确定选定的统计量到底是多少;
最后比较,判断到底是接受还是拒绝原假设