目录
收起
目录
目录
一、SVPWM基本原理
1.从三相电机运行原理到SVPWM调制技术
2.SVPWM调制的实现方法
3.合成参考电压矢量的方法
(abc->αβ坐标变换)
4.基本电压矢量时间的分配
5.基本电压矢量顺序的分配
6.扇区判断
二、仿真验证
1.操作过程
2.仿真文件
一、SVPWM基本原理
1.从三相电机运行原理到SVPWM调制技术
SVPWM调制技术最早是针对交流电机驱动而提出的,因此在分析前先简单回顾三相交流电机的运行原理:

图1 交流电机定子绕组
三相交流电机定子绕组是对称设置的,即A,B,C三相绕组轴线在空间上互差120°电角度。在三相交流电压作用下,绕组中流过三相对称电流 、、��、��、�� ,选取A相电流为基准(设A相电流初相位为零,A相绕组轴线为空间电角度原点),可以写出三相对称电流的表达式:

绕组中的三相对称电流分别在空间中产生脉振磁动势:

其中, ��1 为每相脉振磁动势的基波幅值。
三相的脉振磁动势可以在空间中合成一个幅值不变的旋转波:

磁动势波形绘制如下:
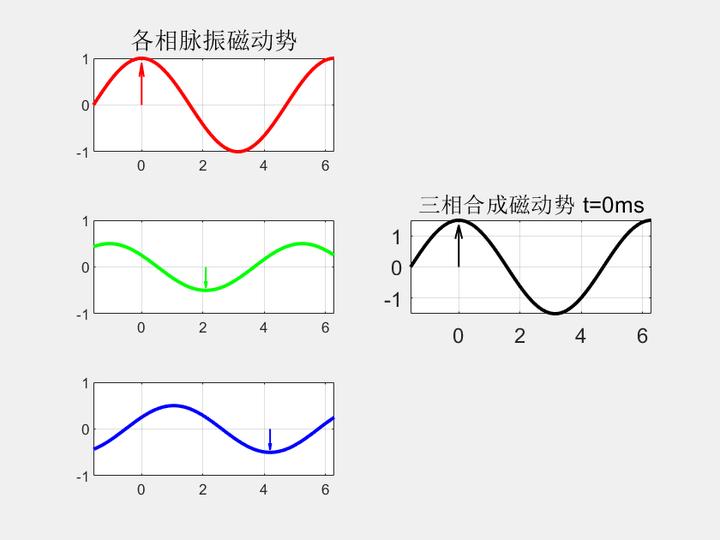
考虑理想情况,即忽略电机的铁损和铜损,三相合成的磁动势可以在空间中产生与它同相的旋转磁场。
这个旋转磁场切割电机转子,在转子绕组中引起感应电流,该电流与旋转磁场相互作用产生电磁转矩,从而驱动交流电机旋转。这就是交流电机的运行原理。
以上是从电磁场的角度分析空间中的旋转磁场,磁动势的表达式是关于时间 � 和空间 � 两个变量的函数,推导较为复杂。而在SVPWM调制中,以复平面中的空间矢量代表磁动势和旋转磁场,从而在复平面中可以直观地显示物理量的变化,下面做具体分析:
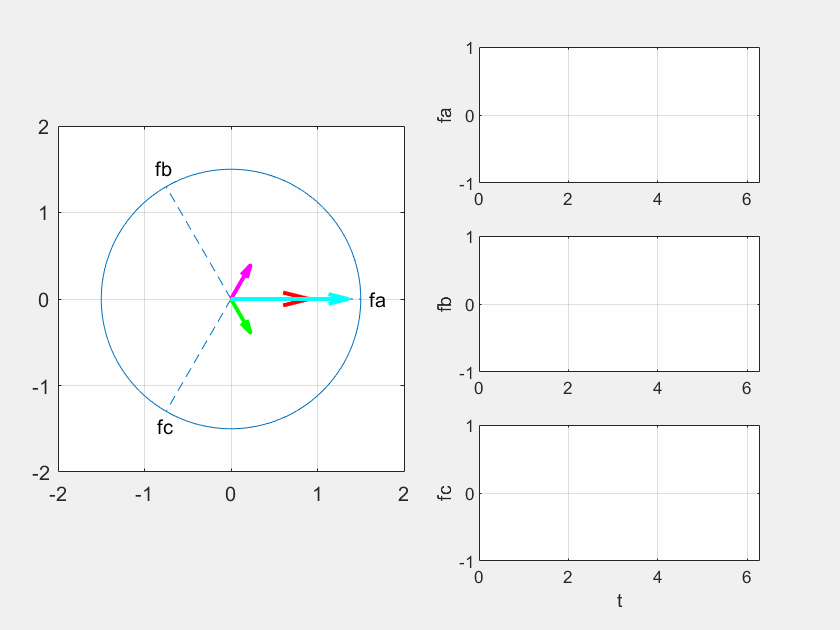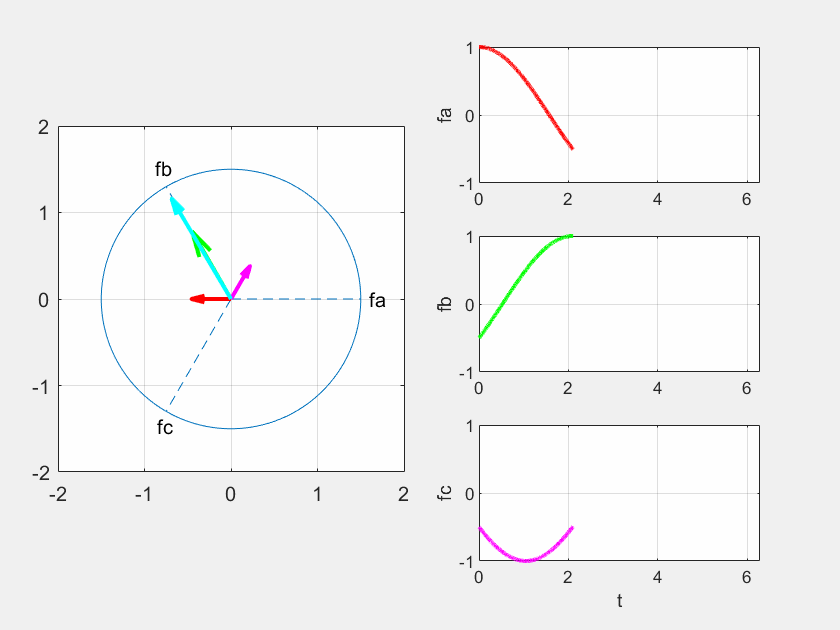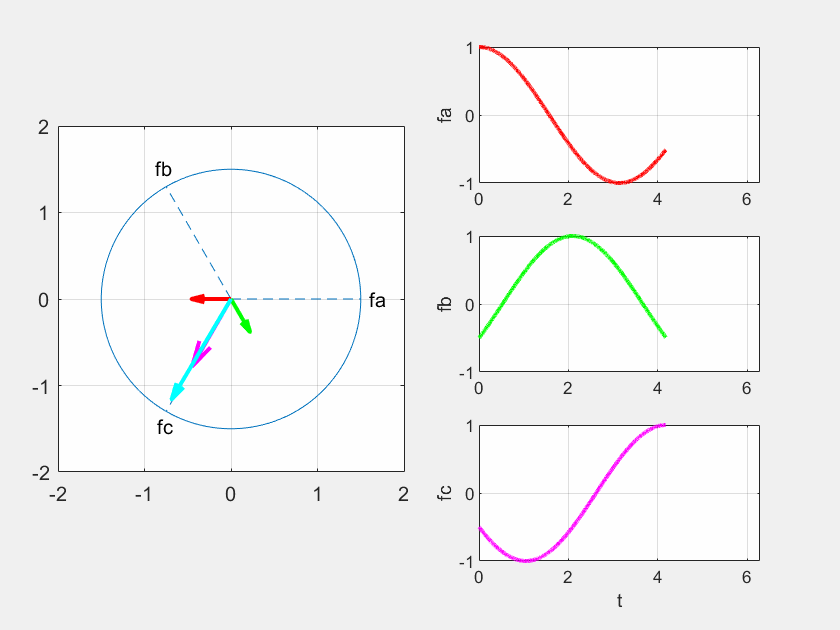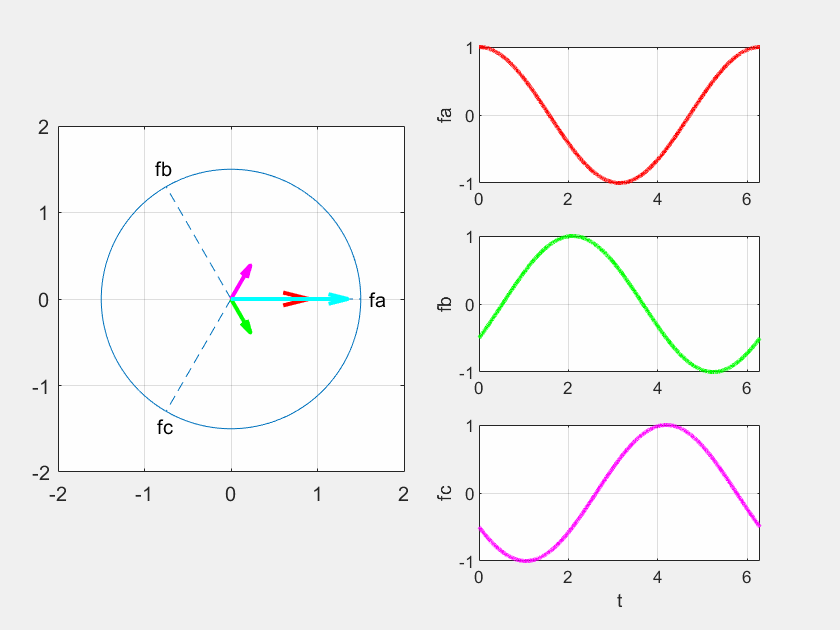
引入空间矢量 、、��¯、��¯、��¯ ,它们分别代表A、B、C相绕组产生的脉振磁动势。空间矢量既有大小,又有方向。 、、��¯、��¯、��¯ 的参考方向分别为A、B、C相绕组轴线方向,大小随电流做正弦变化。写出复平面中空间矢量 、、��¯、��¯、��¯ 的表达式:

引入空间矢量 �1¯ ,代表三相合成磁动势, �1¯ 的表达式为:

由此可知,合成磁动势 �1¯ 幅值不变,在复平面上匀速旋转,它就代表了交流电机三相合成基波磁动势(幅值不变的旋转波)。通过下面的动画,可以直观地理解 、、、��¯、��¯、��¯、�1¯ 之间的关系。
考虑理想情况,忽略电机的铁损和铜损,三相合成的磁动势可以在空间中产生与它同相的旋转磁场,该磁场的磁链可以表示为:

这个旋转磁场切割电机转子,在转子绕组中引起感应电流,该电流与旋转磁场相互作用产生电磁转矩,从而驱动交流电机旋转。
在交流电机中,旋转磁场是通过定子绕组上的三相电压产生的。对于驱动电机的逆变器来说,输出端的电压是可以控制的,只需要使逆变器的输出模拟三相电压的作用效果,就可以驱动电机旋转。因此,逆变器控制的关键在于找到旋转磁场与输入电压之间的关系。(下图为三相电压型逆变器)

图4 逆变器结构
根据电磁感应原理,对磁链的表达式两边求导,得:

由此引入了新的空间矢量 、、、�¯�、�¯�、�¯�、�¯ 。其中, 、、�¯�、�¯�、�¯� 就是加在三相对称绕组上的交流电压,它们的方向分别为绕组轴线方向,大小按照正弦规律变化。空间中三相合成的电压矢量 �¯ 可以由磁链 �¯1 求导得到:

可以看出,合成电压矢量 �¯ 同样是一个空间中幅值不变的旋转矢量,只是它超前磁链 �¯1 90° 的电角度。因此,只要控制逆变器输出端合成的电压矢量 �¯ 为一个旋转矢量,那么空间中就会产生旋转的 �¯1 ,旋转磁场驱动交流电机运行,也就完成了电机驱动器的设计。这就是SVPWM调制的控制目标。

图5 空间矢量参考方向
2.SVPWM调制的实现方法
要实现交流电机的驱动,需要使得逆变器输出端合成电压矢量为一个幅值不变的旋转矢量。因此,首先分析逆变器输出端合成电压矢量的情况。
逆变器结构如下图所示,在三相半桥电路中,由六个开关管控制输出端电压的状态。为了防止短路,同一桥臂的上下两只开关管是互补导通的。因此,只要确定了上桥臂三只开关管的开关状态,就可以确定整个逆变器的工作状态。用 ��=1 和 ��=0 分别代表开关管 �� 的导通和关断,那么用一组数字 ��−��−�� 即可表征逆变器所有的开关管状态。从“000”到“111”,逆变器共有8种工作状态。

图6 三相电压型半桥逆变器
以工作状态 ������=100 为例分析逆变器输出端合成电压矢量的情况。此时,逆变器中的通路如下图所示:

图7 开关状态:100
画出简化电路如下图,根据分压原理,可以计算出每相绕组上的电压矢量,即
、��=23��、��=��=−13��

图8 开关状态:100
根据(图5)中的电压矢量参考方向,可以求出此状态下的合成电压矢量,如图所示:

图9 100状态合成电压矢量
根据二进制编码,将 ������=100 的工作状称为状态4,对应的合成电压矢量为 �4=��∠0° 。类似地,求出逆变器每一个工作状态的合成电压矢量,如下图所示:

图10 各种工作状态的输出结果
八种工作状态中,状态0和状态7合成电压矢量为零矢量,其余六种工作状态合成的电压矢量将平面划分为6个扇区。已知SVPWM的控制目标是在空间中合成旋转的电压矢量,将这个幅值不变,方向随时间变化的电压矢量作为给定参考电压矢量 ���� , ����=����� 。
既然参考矢量 ���� 在空间中旋转,而逆变器输出端能够合成的的8种电压矢量在空间中均匀分布,于是考虑用 �0−�7 8种基本电压矢量来近似合成不同位置的参考电压矢量,从而将输出的合成电压矢量变为一个幅值不变的旋转矢量。这就是SVPWM调制的基本实现方式。
3.合成参考电压矢量的方法
将参考电压矢量 ���� 的旋转过程划分为一系列极短的时间段,每一个时间段持续时间为 �� ,将其称为一个开关周期。在一个开关周期内,近似认为参考电压矢量的方向保持不变。离散化的处理如下图所示:

图11 参考电压矢量旋转过程离散化
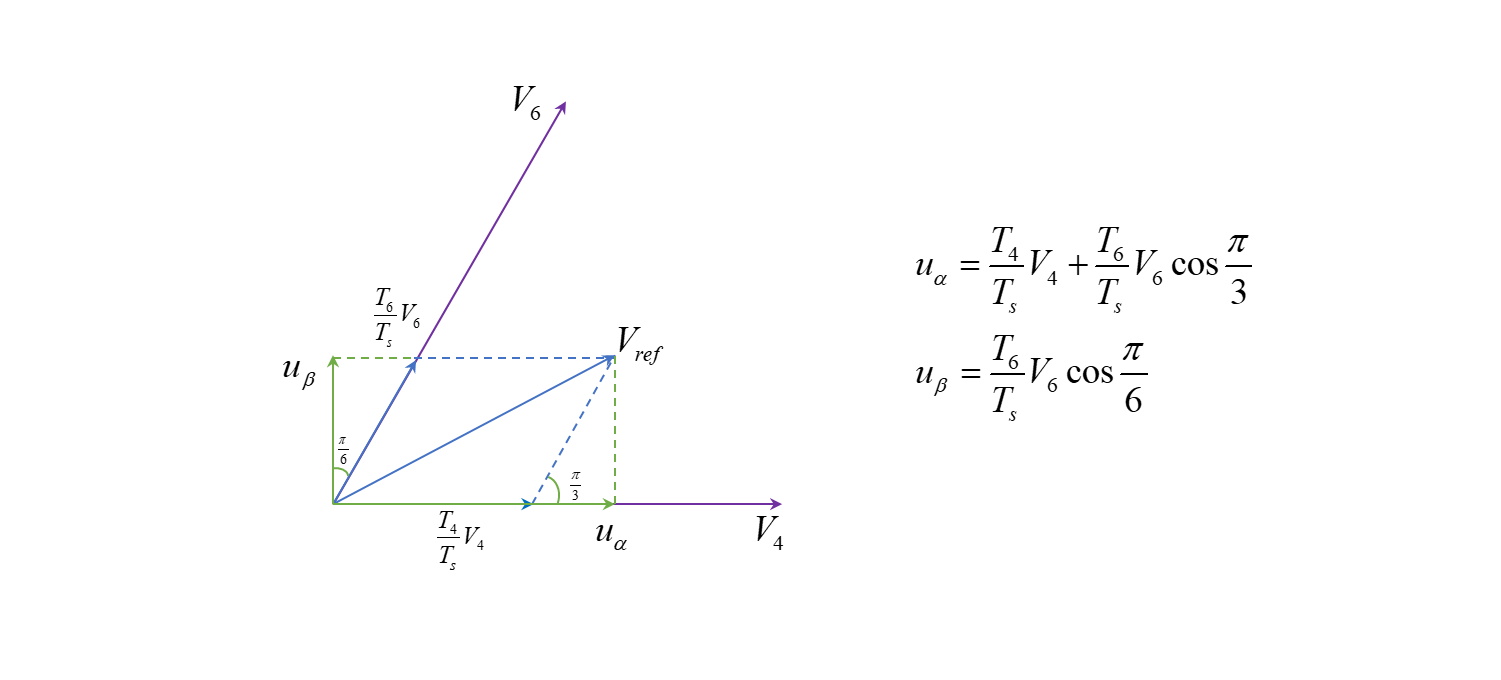
参考电压矢量 ���� 旋转至不同扇区时,由不同的基本电压矢量来合成它。以 ���� 运行在第一扇区为例,由基本电压矢量 、�4、�6 来近似合成它。某一个开关周期内, ���� 的空间位置如下图所示,其相位角为 � 。

图12 第一扇区参考矢量的合成
在这一开关周期 0∼�� 的时间内,使逆变器持续输出基本电压矢量 �4 的时间为 �4 ,持续输出基本电压矢量 �6 的时间为 �6 ,剩余时间 �0=��−(�4+�6) 由零矢量 �0 或 �7 补齐。根据PWM调制技术的面积等效原理,要实现输出结果和参考电压矢量的等效,需要使它们在开关周期 �� 时间内冲量相等,即:

根据矢量合成的平行四边形法则, �4�4�� 即为 ���� 在基本电压矢量 �4 方向上的分量, �6�6�� 即为 ���� 在基本电压矢量 �6 方向上的分量。由此可以计算出 �4 和 �6 的大小。(计算之前,首先在以下分割线中补充一部分坐标变换的内容)
(abc->αβ坐标变换)
参考第一部分“从三相电机运行原理到SVPWM调制技术”的介绍,
三相对称电压 、、��、��、�� 的表达式为:

他们对应的空间电压矢量为:

三相合成的电压矢量为:

以上电压矢量的参考方向,为空间中互差120°的轴线方向,称为“abc坐标系”,也叫“三相静止坐标系”。在SVPWM调制中,常用“两相静止坐标系”,也叫“αβ坐标系”。其中,α轴为复平面中参考矢量 �¯� 的方向,β轴为超前α轴90°的方向。因此,需要做“abc坐标系”到“αβ坐标系”的变换。
采用“αβ坐标系”时,用α、β轴上的分量表示空间电压矢量 �¯ 。因此需要将 �¯ 分解到α、β轴上,即α、β轴上的空间电压矢量 、�¯�′、�¯�′ 合成效果与abc轴上的空间电压矢量 、、�¯�、�¯�、�¯� 的合成效果相同,均为 �¯ 。

坐标变换:三相静止到两相静止
上图所示为空间电压矢量 �¯ 的合成与分解,根据复平面中的运算规律,可直接计算出 、�¯�′、�¯�′ 的大小,即:

写成矩阵形式:

直接对合成电压矢量 �¯=32����� 分解,也可得到 、�¯�′、�¯�′ 的大小:

可以看到,当合成的电压矢量相同时,α、β轴上 、�¯�′、�¯�′ 的幅值是abc轴上 、、�¯�、�¯�、�¯� 的 32 倍。为了后续计算的方便,我们希望α、β轴上空间电压矢量与abc轴上的具有相同的幅值,于是在变换过程中乘一个系数 �=23 ,从而得到 、�¯�、�¯� 。最终的坐标变换为:

总结:为了使坐标变换后得到的 、�¯�、�¯� 与abc坐标系中的 、、�¯�、�¯�、�¯� 幅值相等,在变换过程中乘以系数 �=23 ,这种变换的条件被称为等幅值变换。于是,“αβ坐标系”中合成电压矢量的幅值均变为实际的2/3。在下面的SVPWM调制中,均按照“αβ坐标系”的条件计算。
4.基本电压矢量时间的分配
在“αβ坐标系”,求解第3部分“合成参考电压矢量的方法”中的方程组,得到 �4 和 �6 的大小:

利用αβ轴上的分量进行计算:
在“αβ坐标系”的条件下,合成电压矢量乘以系数m后,幅值均变为实际的2/3。而在(图9)和(图10)中已经计算了逆变器输出基本电压矢量 �0−�7 的实际幅值为 �� ,所以在“αβ坐标系”中,其幅值均按照 23�� 计算,即在上式中代入 �4=�6=23�� ,计算结果为:

ps:需要说明的是,计算时间利用了参考电压矢量与基本电压矢量各分量的比值,而它们在αβ坐标系中均同时变为实际的2/3,所以等幅值变换的系数m对结果没有影响
类似地,可以计算出在不同扇区用两个基本电压矢量合成参考电压矢量时,它们分别的持续时间:
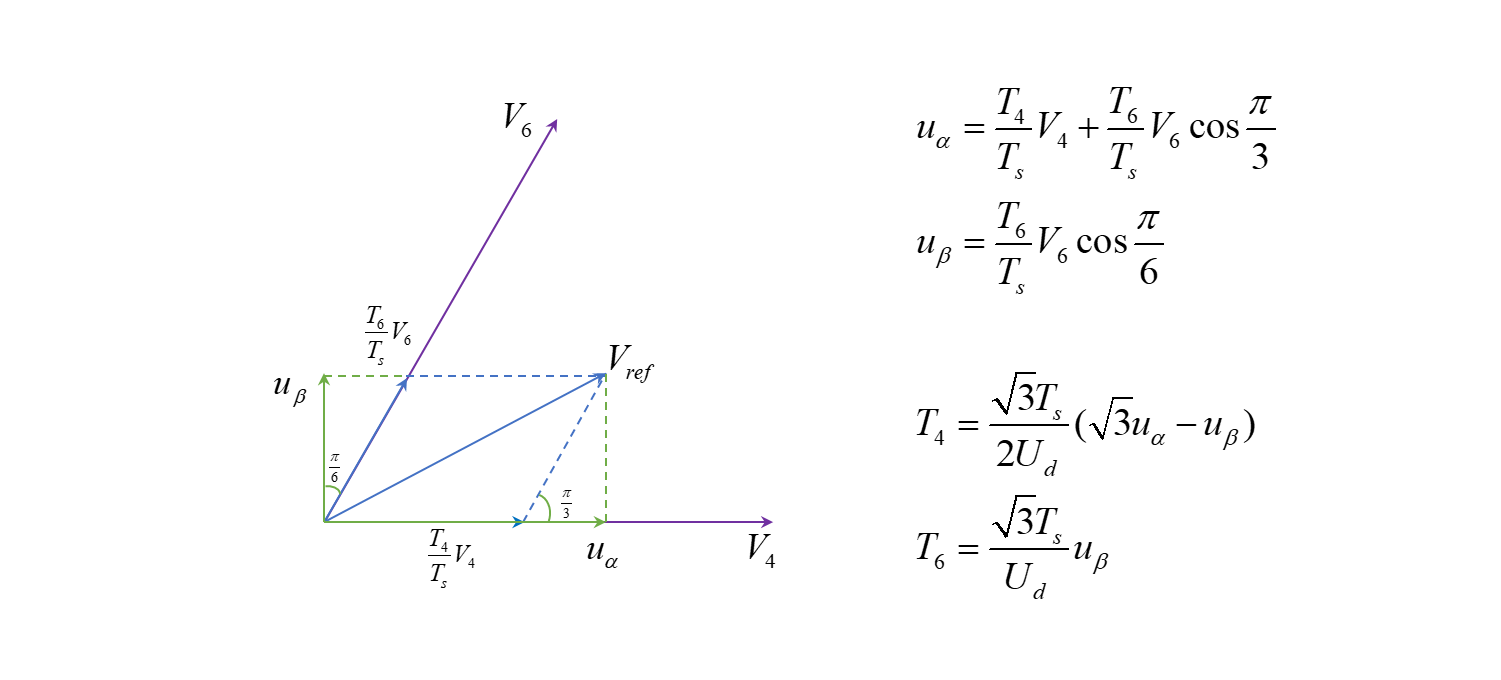
第一扇区
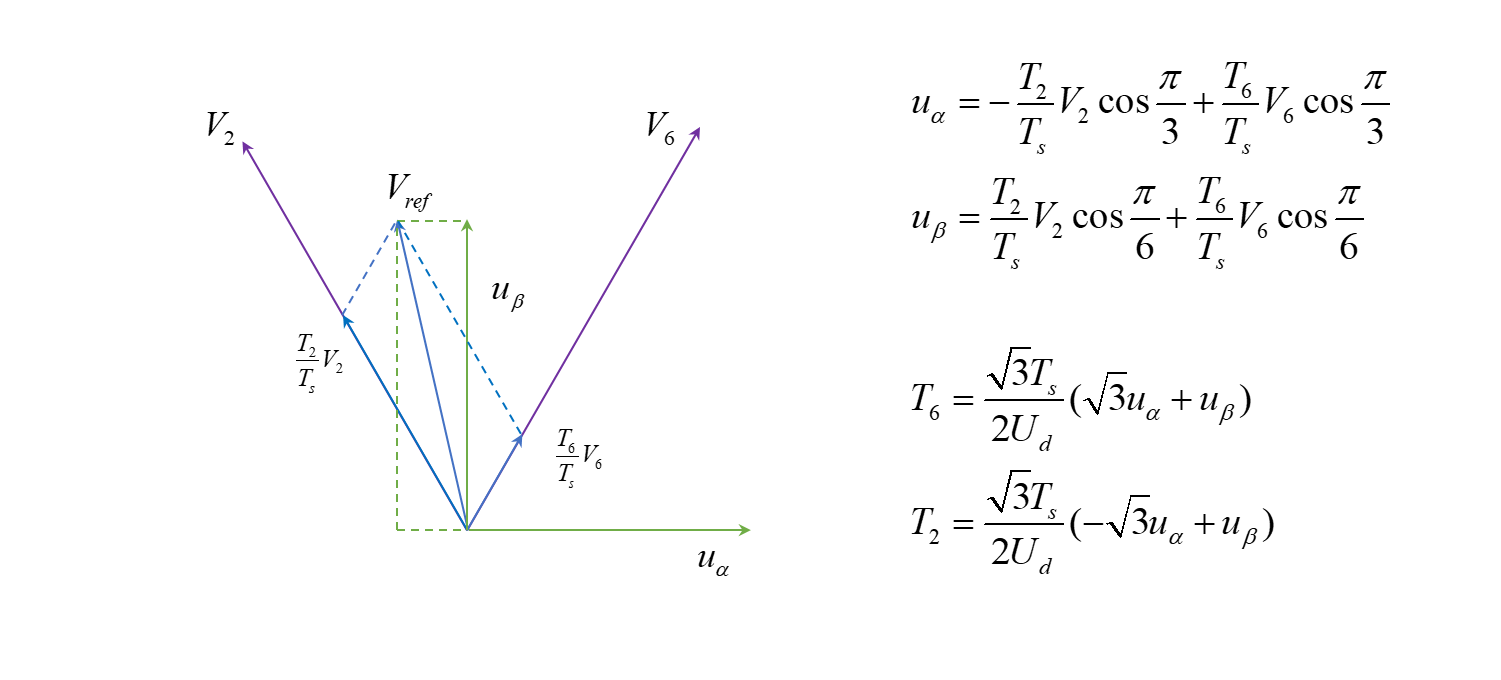
第二扇区
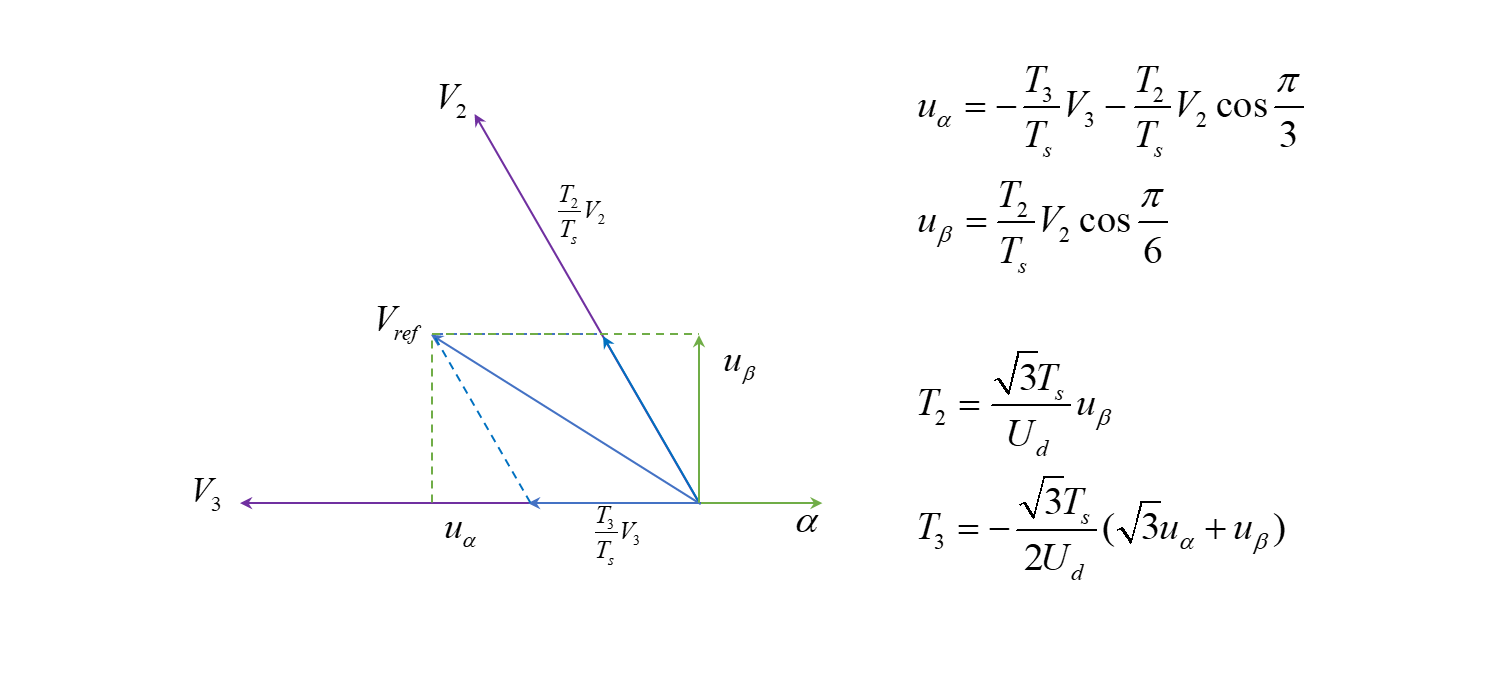
第三扇区
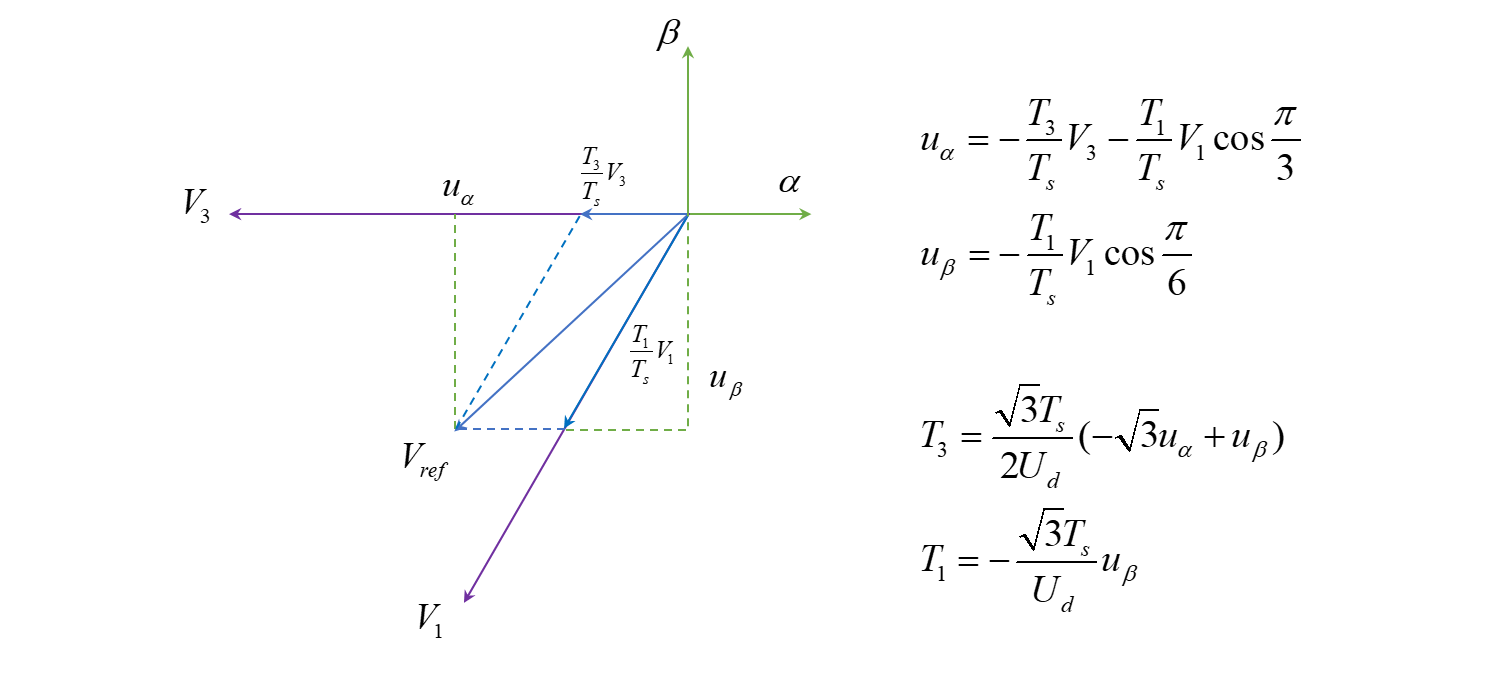
第四扇区

第五扇区
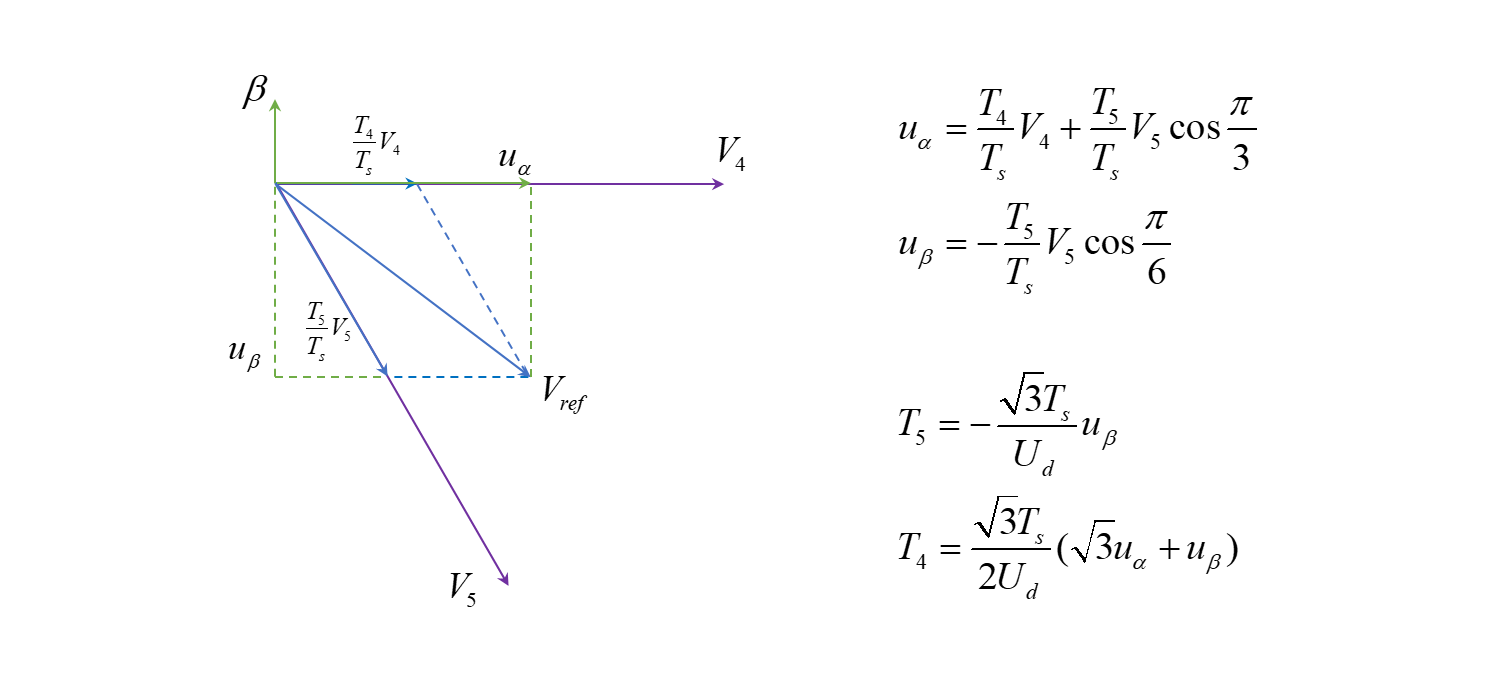
第六扇区
5.基本电压矢量顺序的分配
上一节中计算得出了基本电压矢量的持续时间,以第一扇区为例,在一个开关周期内,逆变器先工作在状态4,输出基本电压矢量 �4 ,持续时间为 �4 ;然后切换开关状态,逆变器工作在状态6,输出基本电压矢量 �6 ,持续时间为 �6 ;剩余时间 �0=��−(�4+�6) ,逆变器工作在状态0或状态7,输出零矢量 �0 或 �7 ,于是根据冲量相等原则,逆变器输出结果等效于参考电压矢量的作用结果。矢量合成的过程如下图所示:

但在这种控制方式中,一个开关周期内只切换了两次开关状态,实际合成的电压矢量对参考电压的等效是比较粗糙的。SVPWM调制中,希望逆变器输出的合成电压矢量尽可能接近参考电压矢量,工程中常用“七段式”或“五段式”输出方式。
对于“七段式”输出方式,仍以第一扇区为例,逆变器的工作状态切换为:状态0->状态4->状态6->状态7->状态6->状态4->状态0。在前半个开关周期,首先逆变器输出零矢量 �0 ,持续时间为 ��−(�6+�4)4=�04 ;接着输出基本电压矢量 �4 ,持续时间为 �42 ;再输出基本电压矢量 �6 ,持续时间为 �62 ;再输出零矢量 �7 ,持续时间为 �04 ;对称地,在后半个开关周期,首先逆变器输出零矢量 �7 ,持续时间为 �04 ;接着输出基本电压矢量 �6 ,持续时间为 �62 ;再输出基本电压矢量 �4 ,持续时间为 �42 ;最后输出零矢量 �7 ,持续时间为 �04 。矢量合成的过程如下图所示:

以上过程可以表示在下图的时间轴中:
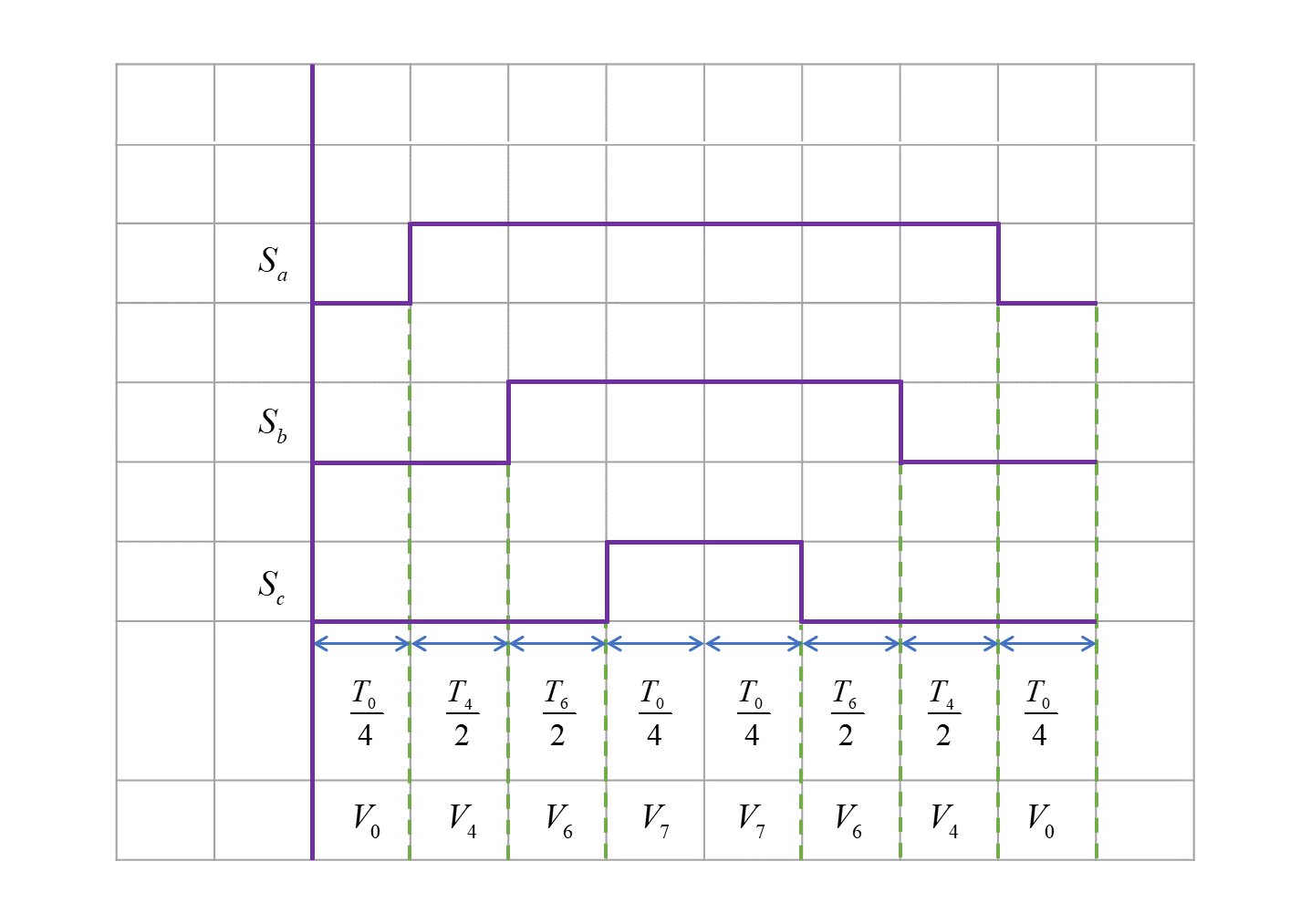
、、��、��、�� 分别代表驱动逆变器上桥臂的PWM信号,PWM信号由给定调制波和三角载波通过比较器输出,于是可以求得三角载波和三个比较器的给定调制波:
ps:此处对应三角载波大于调制波时,PWM信号为“1”,否则为“0”

三角波幅值为 ��2
三个比较器给定调制波分别为:

类似地,计算出每个扇区中的情况:

第一扇区
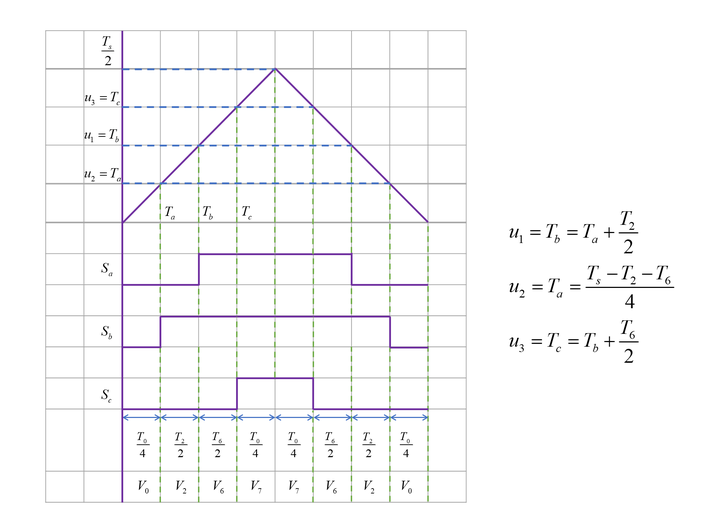
第二扇区

第三扇区
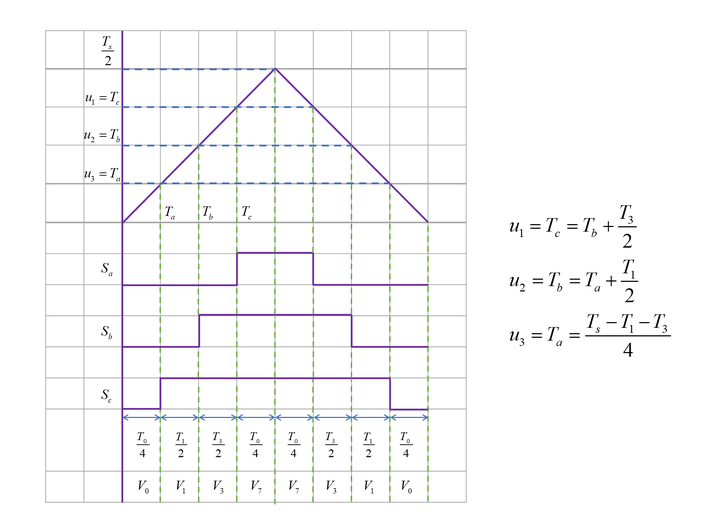
第四扇区

第五扇区
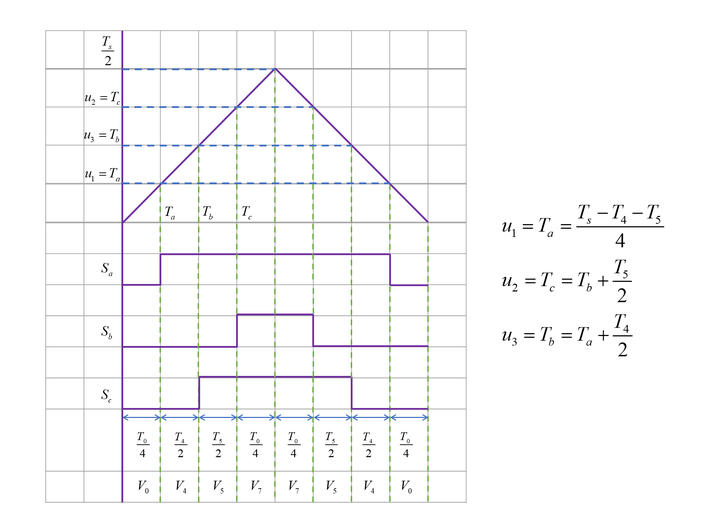
第六扇区
为了后序编程的方便,下面对不同扇区中比较器的参考调制波信号进行归纳。
首先列出各扇区调制波的计算公式,


可以看出,图中相同色块的公式具有相似的形式,为简化计算可将它们归为一类。另外,由于每个扇区只有两个非零矢量参与参考电压矢量的合成,因此所有计算公式中均只用 、�1、�2 表示非零矢量的持续输出时间。
以第一扇区为例,说明简化的过程。取以下计算表达式:

另外,希望时间的表达式中只出现 、�1、�2 ,所以用 �1 代替 �4 , �2 代替 �6 ,简化后为:

类似地,将所有扇区的处理结果归纳如下:


6.扇区判断
六个扇区由三条分界线划分,每条分界线划分区域的条件如下:
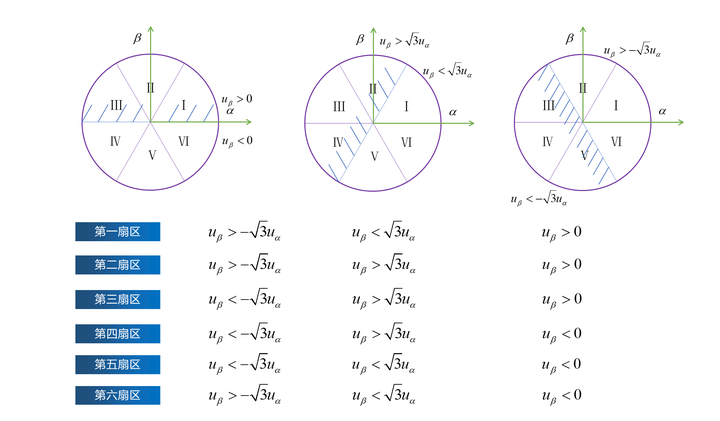
将各扇区使用二进制代码编码如下:
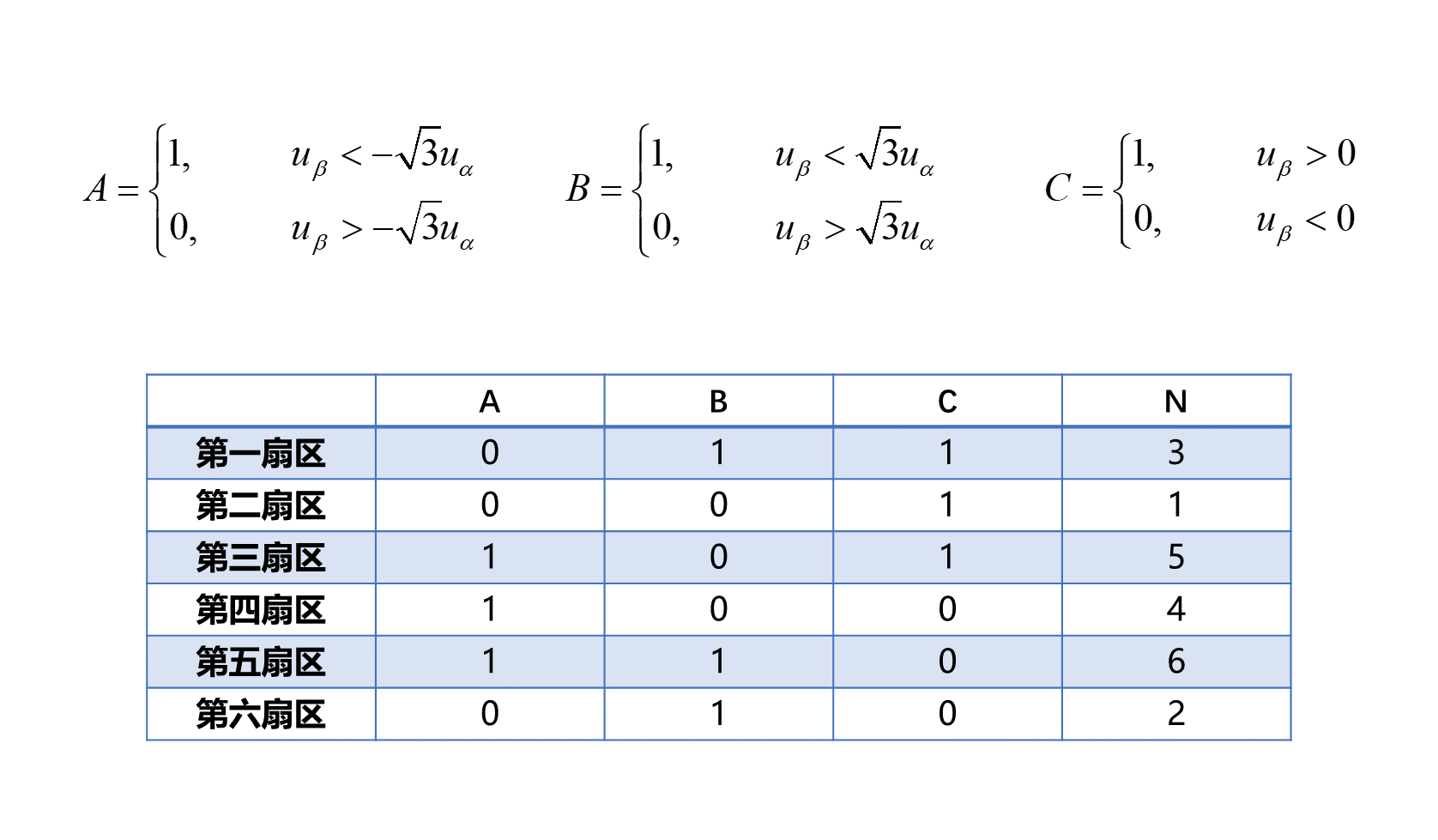
A、B、C为判断参考电压矢量所在扇区的条件,N为该扇区对应的二进制编码。至此,就完成了SVPWM实现方法的介绍。下面通过matlab实现以上步骤,并验证SVPWM调制技术。
二、仿真验证
1.操作过程
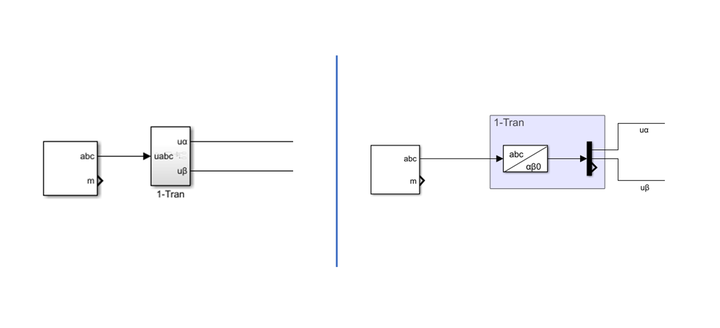
(1)给定参考电压矢量
三相电压合成旋转电压矢量,并变换至“αβ坐标系”:
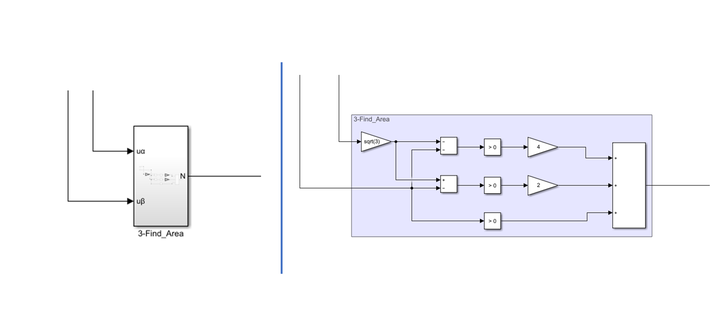
(2)确定参考矢量所在扇区
根据第6节“扇区判断”, �=4⋅�+2⋅�+�
(3)计算中间变量 �,�,�,�1,�2

(4)根据扇区位置确定比较器的参考电压

(5)参考电压与三角载波送入比较器,生成PWM信号
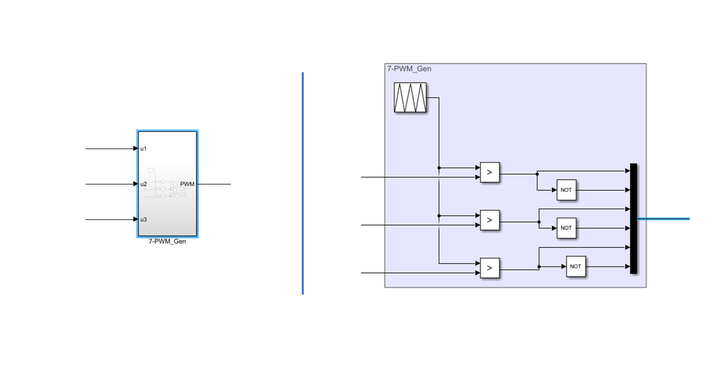
(6)通过PWM信号控制主电路,逆变器输出三相电压
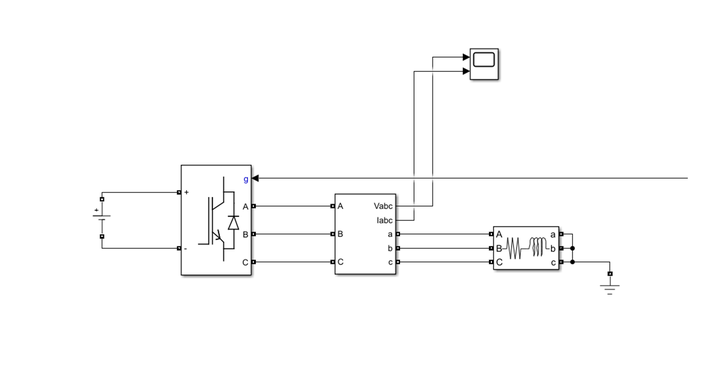
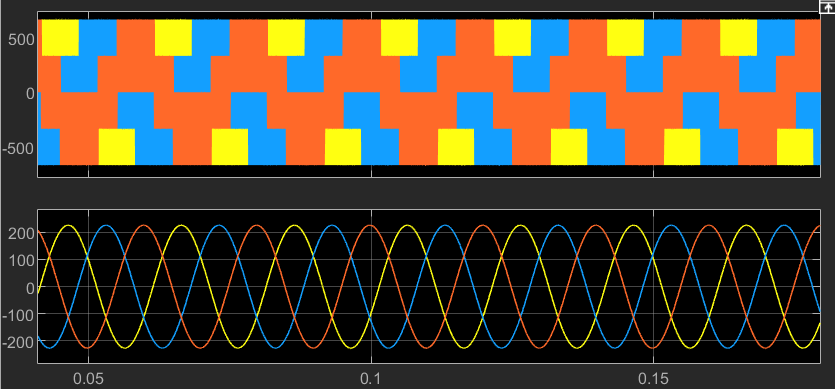
7.仿真结果
2.仿真文件
链接:https://pan.baidu.com/s/1PWJcW5UT34yK8s7EBp7Dqg
提取码:q4mq