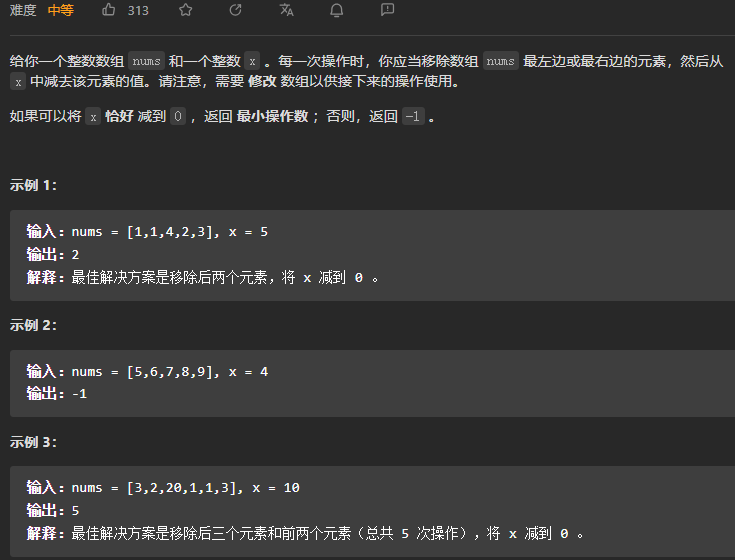
1658.将x减到0的最小操作数
思路与算法:
根据题目描述,在每一次操作中,可以移除数组nums最左边和最右边的元素,因此,在所有的操作完成后,数组nums的一个前缀以及一个后缀被移除,并且它们的和恰好为x,前缀 以及后缀可以为空
记数组的长度为n,可以用left和right分别表示选择的前缀以及后缀的边界,如果left=-1,表示选择了空前缀;如果right=n表示我们选择了空后缀
由于数组nums中的元素均为正数,因此当left向右移动(即前缀的范围增加)时,它们的和是严格递增的,要想将它们的和控制在x,必须将right向右移动,可以用滑动窗口的方法来解决
初始时,left的值为-1,right为0,表示选择了空前缀以及整个数组作为后缀,用lsum和rsum分别记录前缀以及后缀的和,那么:
- 如果lsum + rsum = x,说明我们找到了一组答案,对应的操作次数为(left+1)+(n-right)
- 如果lsum + rsum > x,说明和过大,需要将right向右移动一个位置
- 如果lsum + rsum < x,说明和过小,需要将left向右移动一个位置
class Solution {
public int minOperations(int[] nums, int x) {
int n = nums.length;
int sum = Arrays.stream(nums).sum(); //数组总和
if(sum < x){
return -1;
}
//left和right为选择的前缀和后缀的边界
int right = 0;
int lsum = 0,rsum = sum; //lsum和rsum分别表示前缀和和后缀和
int ans = n + 1;
for(int left = -1 ; left < n ; left++){
if(left != -1){
lsum += nums[left];
}
while(right < n && lsum + rsum > x){ //和过大,需要将right向右移动一个位置
rsum -= nums[right];
++right;
}
if(lsum + rsum == x){
ans = Math.min(ans,(left + 1) + (n - right));
}
}
return ans > n ? -1:ans;
}
}