【算法】最短路径——迪杰斯特拉 (Dijkstra) 算法

news2024/10/7 8:30:12

目录

  • 1.概述
  • 2.代码实现
    • 2.1.节点类
    • 2.2.邻接矩阵存储图
    • 2.3.邻接表存储图
    • 2.4.测试
  • 3.扩展
    • 3.1.只计算一对顶点之间的最短路径
    • 3.2.获取起点到其它节点具体经过的节点
  • 4.应用

本文参考：
LABULADONG 的算法网站

1.概述

（1）在图论中，最短路径是指在加权图中两个顶点之间长度最短的路径，这个路径的长度是每条边的权重之和。在现实生活中，可以将图中的顶点表示为地点，将边表示为这些地点之间的道路或交通线路，把每条边的权重定义为行程时间、行驶距离、经济成本、能源消耗等相应的度量单位。在这种情况下，最短路径问题就是为了找到从一个地点到另一个地点的最快、最短、最便宜、最节能的路径。最短路径问题在计算机科学和运筹学方面非常重要，它可以解决很多现实问题，如网页排名算法、路由算法、航班调度、电信网络建设等。Dijkstra 算法是解决最短路径问题的经典算法之一。

（2）迪杰斯特拉算法 (Dijkstra) 是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

（3）实现 Dijkstra 算法的一种基本思路如下：

  • 维护一个待确定最短路径的节点的集合，初始时只有起点。之后，每次从这个集合中取出一个节点，更新它所有邻居的距离，将它们加入这个集合中。具体实现中，使用一个优先队列来存储待访问的节点，并按照最短距离从小到大的顺序进行访问。
  • 在代码中，使用一个数组 dist 来记录起点到每个节点的最短距离，同时使用一个自定义的 Node 类来表示所有待访问的节点，并存储其与起点的距离。算法主体部分由一个 while 循环实现。每次取出队列中距离最小的节点，并遍历其所有邻居，更新起点到每个邻居的距离，然后将未确定最短路径的点加入队列中。

常数较小的情况下，Dijkstra 算法的时间复杂度为 O(ElogV)，其中 E 为边数，V 为顶点数。

2.代码实现

2.1.节点类

class Node {
    //图中当前节点的 id
    int id;
    //从 start 节点到当前节点的距离
    int distFromStart;

    public Node(int id, int distFromStart) {
        this.id = id;
        this.distFromStart = distFromStart;
    }
}

2.2.邻接矩阵存储图

class Solution {
    /*
		start: 起点
		graph: 用于表示图的邻接矩阵
		返回值: 起点到图中每一个点的最短距离
	*/
    public int[] dijkstra(int start, int[][] graph) {
        // dist[i] 表示起点 start 到节点 i 的最短路径长度
        int[] dist = new int[graph.length];
        // dist[i] = Integer.MAX_VALUE 表示起点到节点 i 之间不可达
        Arrays.fill(dist, Integer.MAX_VALUE);
        //起点与自己之间的最短路径长度为 0
        dist[start] = 0;
        //自定义优先级队列规则，distFromStart 值较小的节点排在队首
        Queue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(a -> a.distFromStart));
        queue.offer(new Node(start, 0));
        while (!queue.isEmpty()) {
            //取出队首元素
            Node node = queue.poll();
            int id = node.id;
            int curDistFromStart = node.distFromStart;
            if (curDistFromStart > dist[id]) {
                continue;
            }
            //将与当前节点相邻的所有节点存入队列
            for (int i = 0; i < graph[id].length; i++) {
                if (graph[id][i] != Integer.MAX_VALUE) {
                    int distToNextNode = dist[id] + graph[id][i];
                    // 更新 dist
                    if (dist[i] > distToNextNode) {
                        dist[i] = distToNextNode;
                        queue.offer(new Node(i, distToNextNode));
                    }
                }
            }
        }
        return dist;
    }
}

2.3.邻接表存储图

class Solution {
    /*
		start: 起点
		graph: 用于表示图的邻接表
		返回值: 起点到图中每一个点的最短距离
	*/
    public int[] dijkstra(int start, List<int[]>[] graph) {
        // dist[i] 表示起点 start 到节点 i 的最短路径长度
        int[] dist = new int[graph.length];
        // dist[i] = Integer.MAX_VALUE 表示起点到节点 i 之间不可达
        Arrays.fill(dist, Integer.MAX_VALUE);
        //起点与自己之间的最短路径长度为 0
        dist[start] = 0;
        //自定义优先级队列规则，distFromStart 值较小的节点排在队首
        Queue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(a -> a.distFromStart));
        queue.offer(new Node(start, 0));
        while (!queue.isEmpty()) {
            //取出队首元素
            Node node = queue.poll();
            int id = node.id;
            int curDistFromStart = node.distFromStart;
            if (curDistFromStart > dist[id]) {
                continue;
            }
            //将与当前节点相邻的所有节点存入队列
            for (int[] neighbor : graph[id]) {
                int nextNodeID = neighbor[0];
                int distToNextNode = dist[id] + neighbor[1];
                //更新 dist
                if (dist[nextNodeID] > distToNextNode) {
                    dist[nextNodeID] = distToNextNode;
                    queue.offer(new Node(nextNodeID, distToNextNode));
                }
            }
        }
        return dist;
    }
}

2.4.测试

（1）本测试中的加权无向图如下所示，并且设置起点为 0。

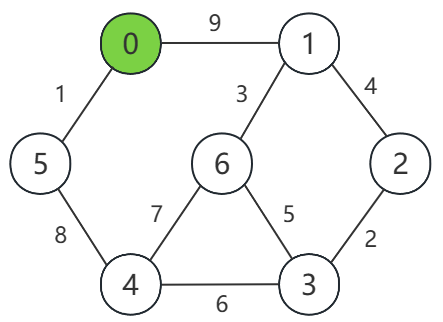
在这里插入图片描述

（2）邻接矩阵的测试代码如下：

class Test {
	public static void main(String[] args) {
        //图的顶点数
        int n = 7;
        int[][] graph = new int[n][n];
        //初始化邻接矩阵，初始化为 Integer.MAX_VALUE 表示不可达
        for (int i = 0; i < n; i++) {
            Arrays.fill(graph[i], Integer.MAX_VALUE);
        }
        //添加图的边
        graph[0][1] = 9;
        graph[0][5] = 1;
        graph[1][0] = 9;
        graph[1][2] = 4;
        graph[1][6] = 3;
        graph[2][1] = 4;
        graph[2][3] = 2;
        graph[3][2] = 2;
        graph[3][4] = 6;
        graph[3][6] = 5;
        graph[4][3] = 6;
        graph[4][5] = 8;
        graph[4][6] = 7;
        graph[5][0] = 1;
        graph[5][4] = 8;
        graph[6][1] = 3;
        graph[6][3] = 5;
        graph[6][4] = 7;

        Solution solution = new Solution();
        int start = 0;
        int[] distances = solution.dijkstra(start, graph);
        System.out.println(Arrays.toString(distances));
    }
}

输出结果如下：

[0, 9, 13, 15, 9, 1, 12]

（3）邻接表的测试代码如下：

class Test {
	public static void main(String[] args) {
        //图的顶点数
        int n = 7; 
        List<int[]>[] graph = new ArrayList[n];
        //初始化邻接表
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        //添加图的边
        graph[0].add(new int[]{1, 9});
        graph[0].add(new int[]{5, 1});
        graph[1].add(new int[]{0, 9});
        graph[1].add(new int[]{2, 4});
        graph[1].add(new int[]{6, 3});
        graph[2].add(new int[]{1, 4});
        graph[2].add(new int[]{3, 2});
        graph[3].add(new int[]{2, 2});
        graph[3].add(new int[]{4, 6});
        graph[3].add(new int[]{6, 5});
        graph[4].add(new int[]{3, 6});
        graph[4].add(new int[]{5, 8});
        graph[4].add(new int[]{6, 7});
        graph[5].add(new int[]{0, 1});
        graph[5].add(new int[]{4, 8});
        graph[6].add(new int[]{1, 3});
        graph[6].add(new int[]{3, 5});
        graph[6].add(new int[]{4, 7});

        Solution solution = new Solution();
        int start = 0;
        int[] distances = solution.dijkstra(start, graph);
        System.out.println(Arrays.toString(distances));
    }
}

输出结果如下：

[0, 9, 13, 15, 9, 1, 12]

3.扩展

3.1.只计算一对顶点之间的最短路径

如果现在只需计算起点 start 到终点 end 的最短路径，那么只需要简单修改上述代码即可，以用邻接表存储图的代码为例：

class Solution {
	/*
		start: 起点
		graph: 用于表示图的邻接矩阵
		返回值: 起点 start 到终点 end 的最短路径
	*/
    public int dijkstra(int start, int end, int[][] graph) {
    
        //...
        
        while (!queue.isEmpty()) {
            //取出队首元素
            Node node = queue.poll();
            int id = node.id;
            int curDistFromStart = node.distFromStart;

            //添加如下代码：如果遍历到 end，直接返回 curDistFromStart 即可
            if (id == end) {
                return curDistFromStart;
            }

            if (curDistFromStart > dist[id]) {
                continue;
            }
            
            //... 
        }
        //如果运行到这里，说明 start 到 end 之间不可达
        return Integer.MAX_VALUE;
    }
}

3.2.获取起点到其它节点具体经过的节点

（1）如果需要找到起点到其余节点的最短路径中依次经过的节点，可以在 Dijkstra 算法中添加一个 prev 数组或 map，记录节点i的前一个访问过的节点 j。在更新 dist[i] 的同时，同时更新 prev[i] = j。最后，通过回溯 prev 数组，可以从目标节点往回遍历，找到最短路径上的所有节点。具体来说，可以按以下步骤实现：

  • 初始化 prev 数组，将所有节点的前继节点都设置为起点。
  • 在更新 dist[i] 的同时，同时更新 prev[i] = j。
  • 当所有节点都处理完毕后，就可以从目标节点往回遍历 prev 数组，找到最短路径上的所有节点。

（2）以用邻接表存储图的代码为例，具体代码如下所示：

class Solution {
	/*
		start: 起点
		graph: 用于表示图的邻接表
		返回值: 起点到图中每一个点的最短距离依次所经过的节点
	*/
    public List<List<Integer>> findShortestPaths(int start, List<int[]>[] graph) {
        int n = graph.length;
        int[] dist = new int[n];
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[start] = 0;
        int[] prev = new int[n];
        Arrays.fill(prev, start);
        Queue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(a -> a.distFromStart));
        queue.offer(new Node(start, 0));
        while (!queue.isEmpty()) {
            Node node = queue.poll();
            int id = node.id;
            int curDistFromStart = node.distFromStart;
            if (curDistFromStart > dist[id]) {
                continue;
            }
            for (int[] neighbor : graph[id]) {
                int nextNodeID = neighbor[0];
                int distToNextNode = dist[id] + neighbor[1];
                if (dist[nextNodeID] > distToNextNode) {
                    //在更新 dist[nextNodeID] 时，同时更新 prev[nextNodeID]
                    dist[nextNodeID] = distToNextNode;
                    prev[nextNodeID] = id;
                    queue.offer(new Node(nextNodeID, distToNextNode));
                }
            }
        }

        //通过 prev 数组回溯路径
        List<List<Integer>> paths = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            List<Integer> path = new ArrayList<>();
            int curNode = i;
            while (curNode != start) {
                path.add(curNode);
                curNode = prev[curNode];
            }
            path.add(start);
            Collections.reverse(path);
            paths.add(path);
        }
        return paths;
    }
}

（3）测试代码如下：

class Solution {
	public static void main(String[] args) {
        //图的顶点数
        int n = 7;
        List<int[]>[] graph = new ArrayList[n];
        //初始化邻接表
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        //添加图的边
        graph[0].add(new int[]{1, 9});
        graph[0].add(new int[]{5, 1});
        graph[1].add(new int[]{0, 9});
        graph[1].add(new int[]{2, 4});
        graph[1].add(new int[]{6, 3});
        graph[2].add(new int[]{1, 4});
        graph[2].add(new int[]{3, 2});
        graph[3].add(new int[]{2, 2});
        graph[3].add(new int[]{4, 6});
        graph[3].add(new int[]{6, 5});
        graph[4].add(new int[]{3, 6});
        graph[4].add(new int[]{5, 8});
        graph[4].add(new int[]{6, 7});
        graph[5].add(new int[]{0, 1});
        graph[5].add(new int[]{4, 8});
        graph[6].add(new int[]{1, 3});
        graph[6].add(new int[]{3, 5});
        graph[6].add(new int[]{4, 7});

        Solution solution = new Solution();
        int start = 4;
        List<List<Integer>> paths = solution.findShortestPaths(start, graph);
        for (int i = 0; i < n; i++) {
            System.out.println("从节点 " + start + " 到节点 " + i +
                    " 的最短距离经过的节点依次为: " + paths.get(i));
        }
    }
}

输出结果如下：

从节点 4 到节点 0 的最短距离经过的节点依次为: [4, 5, 0]
从节点 4 到节点 1 的最短距离经过的节点依次为: [4, 6, 1]
从节点 4 到节点 2 的最短距离经过的节点依次为: [4, 3, 2]
从节点 4 到节点 3 的最短距离经过的节点依次为: [4, 3]
从节点 4 到节点 4 的最短距离经过的节点依次为: [4]
从节点 4 到节点 5 的最短距离经过的节点依次为: [4, 5]
从节点 4 到节点 6 的最短距离经过的节点依次为: [4, 6]

4.应用

（1）Dijkstra算法是一种用于解决单源最短路径问题的算法。它可以帮助找到从一个源节点到图中所有其他节点的最短路径。这个算法广泛应用于许多领域，包括以下几个方面：

  • 网络路由：Dijkstra 算法在网络路由中被广泛使用，用于计算最短路径来传输数据包。
  • 交通规划：Dijkstra 算法可以用于交通网络中的最短路径规划，例如在城市道路网络中找到最短驾驶路线。
  • 电信网络：Dijkstra 算法可以用于计算通信网络中的最短路径，例如电话网络或互联网中的数据包传输。
  • 地理信息系统 (GIS)：Dijkstra 算法可以用于计算地理信息系统中的最短路径，例如导航系统中找到最佳行驶路径。
  • 运输和物流：Dijkstra 算法可以用于解决运输和物流问题，例如货物配送中最优路径的规划。

（2）大家可以去 LeetCode 上找相关的 Dijkstra 算法的题目来练习，或者也可以直接查看 LeetCode算法刷题目录 (Java) 这篇文章中的最短路径章节。如果大家发现文章中的错误之处，可在评论区中指出。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1211605.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

小DEMO：在vue中自定义range组件

小DEMO：在vue中自定义range组件

1、组件样式 2、使用 import cSlider from /components/c-slider/c-slider.vue<div class"range"><cSlider v-model"cScale" change"cScaleChange" :min"1" :max"10"/> </div> 3、组件代码 <templa…
阅读更多...
VS2022配置wxWidgets 3.0.5

VS2022配置wxWidgets 3.0.5

Downloads - wxWidgets下载Windows ZIP 解压进入E:\SoftWare\wxWidgets-3.0.5\build\msw&#xff0c;用VS2022打开wx_vc12.sln&#xff0c;选择生成——批生成&#xff0c;最终生成一些文件 打开VS2022&#xff0c;新建属性表&#xff0c;在属性表里设置&#xff1a; c——常规…
阅读更多...
百度搜索智能化算力调控分配方法

百度搜索智能化算力调控分配方法

作者 | 泰来 导读 随着近年深度学习技术的发展&#xff0c;搜索算法复杂度不断上升&#xff0c;算力供给需求出现了爆发式的增长。伴随着AI技术逐步走到深水区&#xff0c;算法红利在逐步消失&#xff0c;边际效应日益显著&#xff0c;算力效能的提升尤为重要&#xff0c;同时随…
阅读更多...
海报设计必备！五个免费网站分享，让你的创意得以充分展现！

海报设计必备！五个免费网站分享，让你的创意得以充分展现！

海报作为一种重要的宣传工具&#xff0c;在各种场合得到了广泛的应用。然而&#xff0c;对许多人来说&#xff0c;制作一张漂亮的海报并不容易。幸运的是&#xff0c;有许多免费的海报制作网站可以帮助人们轻松地制作出漂亮的海报。本文将分享五个优秀的免费海报制作网站。 1.…
阅读更多...
天津专升本新版报名系统网上报名、填志愿、缴费、审核等操作步骤

天津专升本新版报名系统网上报名、填志愿、缴费、审核等操作步骤

天津高职升本网上报名、填报志愿新版专升本报名系统 ▏报名入口&#xff1a;www.zhaokao.net▏注意&#xff1a;一定要在截止时间内完成报名、填报志愿、缴费、审核、下载《报名信息表》等4步骤▏可报考院校及专业请参考招生院校发布的通知&#xff08;招生简章、报考须知&…
阅读更多...
实时level2访问与策略研发

实时level2访问与策略研发

本周四下午4点&#xff0c;天软会聚焦“实时&level2访问与策略研发”开展我们的天软高频时序数仓会议&#xff0c;本次会议的报名客户&#xff0c;可以申请试用LEVEL-2数据测试账号哦~
阅读更多...
jeesite 按部门过滤数据权限(保姆级图文教程)

jeesite 按部门过滤数据权限(保姆级图文教程)

文章目录 前言一、数据库表添加机构字段二、修改实体3.修改服务层总结前言 在项目开发过程中，数据需要按照部门、公司进行权限过滤，本篇文章记录下如何修改按部门进行权限过滤的详细图文教程。 一、数据库表添加机构字段 要进行权限过滤的表中添加机构字段 二、修改实体 添…
阅读更多...
考研分享第3期 | 211本378分上岸大连理工电子信息经验贴

考研分享第3期 | 211本378分上岸大连理工电子信息经验贴

考研分享第3期 | 211本378分上岸大连理工电子信息经验贴 一、个人信息 姓名&#xff1a;Ming 本科院校&#xff1a;某211学校电子信息工程学院 电子科学与技术专业 上岸院校&#xff1a;大连理工大学 电子信息与电气工程学部 电子信息&#xff08;0854&#xff09; 择校意…
阅读更多...
【案例】由coredump引起的思考：程序的加载流程

【案例】由coredump引起的思考：程序的加载流程

背景 小米项目的同事&#xff0c;最近遇到了一个crash问题&#xff0c;困扰较久&#xff0c;向我请求帮助。&#xff08;其实是客户指定要求我来分析这个问题&#xff0c;该项目之前是由我负责的&#xff0c;帮客户解决很多较多crash问题。估计是实力得到了客户认可吧&#xff…
阅读更多...
数据中心：精密空调监控，这招太高效了！

数据中心：精密空调监控，这招太高效了！

在当今日益复杂的工业环境中&#xff0c;精密空调系统的监控和管理变得至关重要。随着科技的迅猛发展&#xff0c;各行各业对温度、湿度和空气质量等参数的高度控制需求不断增加。 精密空调监控系统通过实时数据采集、分析和反馈&#xff0c;为企业提供了可靠的手段来确保生产环…
阅读更多...
如何借助测评系统实现速卖通店铺补单，吸引更多消费者？

如何借助测评系统实现速卖通店铺补单，吸引更多消费者？

在速卖通平台上&#xff0c;为店铺增加权重和排名是吸引更多买家和提升销售的关键。以下是一些有效的方法&#xff0c;帮助你提升速卖通店铺的权重和排名&#xff1a; 1. 优化商品信息&#xff1a;确保商品标题简洁明了、描述准确详细、图片清晰精美。使用关键词描述&#xff…
阅读更多...
FPGA电平标准的介绍

FPGA电平标准的介绍

对FPGA的管脚进行约束的时候&#xff0c;常常看到这样的电平标准&#xff0c;例如LVCOM18&#xff0c;LVCOS25&#xff0c;LVDS&#xff0c;LVDS25等等&#xff0c;其实这些都是一系列的电平标准。 针对数字电路而言&#xff0c;数字电路表示电平的只有1和0两个状态&#xff0c…
阅读更多...
双十一买高画质投影仪，当贝F6还是极米H6?

双十一买高画质投影仪，当贝F6还是极米H6?

如果你想购买一台4K画质的投影仪,那么在各大平台搜索“双十一最值得买的4K投影仪”时,一定会注意到当贝F6和极米H6这两个型号投影仪。个人认为当贝F6和极米H6都分别是当贝和极米两个品牌非常具有性价比的4K投影仪。那么到底哪一台更适合你。 首先放一张参数对比图,方便参数控研…
阅读更多...
人力物力和时间资源有限？守住1个原则，精准覆盖所有兼容性测试！

人力物力和时间资源有限？守住1个原则，精准覆盖所有兼容性测试！

随着 APP 应用范围越来越广&#xff0c;用户群体越来越大&#xff0c;终端设备的型号也越来越多&#xff0c;移动终端碎片化加剧&#xff0c;使得 APP 兼容性测试成为测试质量保障必须要考虑的环节。 APP 兼容性测试通常会考虑&#xff1a;操作系统、厂家 ROM、屏幕分辨率、网…
阅读更多...
全方位移动机器人 Stanley 轨迹跟踪 Gazebo 仿真

全方位移动机器人 Stanley 轨迹跟踪 Gazebo 仿真

全方位移动机器人 Stanley 轨迹跟踪 Gazebo 仿真 本来打算今天出去跑一下 GPS&#xff0c;但是下雨&#xff0c;作罢 添加参考轨迹信息 以下三个功能包不需要修改&#xff1a; mrobot&#xff1a;在 Rviz 和 Gazebo 中仿真机器人cmd_to_mrobot&#xff1a;运动学解算&#…
阅读更多...
【C++ std::max_element std::min_element std::minmax_element】

【C++ std::max_element std::min_element std::minmax_element】

一 、std::max_element 寻找范围 [first, last) 中的最大元素。 (1) 用 operator< 比较元素。 (3) 用给定的二元比较函数 comp 比较元素。 (2),(4) 同 (1,3) &#xff0c;但按照 policy 执行。这些重载仅若 std::is_execution_policy_v<std::decay_t > (C20 前)std:…
阅读更多...
Alter database open fails with ORA-00600 kcratr_nab_less_than_odr

Alter database open fails with ORA-00600 kcratr_nab_less_than_odr

Alter database open fails with ORA-00600 kcratr_nab_less_than_odr (Doc ID 1296264.1)​编辑To Bottom APPLIES TO: Oracle Database - Enterprise Edition - Version 11.2.0.1 to 11.2.0.1 [Release 11.2] Oracle Database - Enterprise Edition - Version 12.1.0.1 to …
阅读更多...
【精彩回顾】 用sCrypt在Bitcoin上构建智能合约（1）

【精彩回顾】 用sCrypt在Bitcoin上构建智能合约（1）

2023年3月24日&#xff0c;sCrypt在英国Exeter大学举办了关于智能合约的大学讲学。sCrypt首席执行官刘晓晖做了题为“用sCrypt在Bitcoin上构建智能合约”的演讲&#xff0c;并与到场的老师、学生进行了深入交流、互动。这次课程着重讲解了 BSV 智能合约的基础概念&#xff0c;以…
阅读更多...
Java学习笔记（七）——面向对象编程（中级）

Java学习笔记（七）——面向对象编程（中级）

一、IDEA &#xff08;一&#xff09;常用的快捷键 &#xff08;二&#xff09;模版/自定义模版 二、包 &#xff08;一&#xff09;包的命名 &#xff08;二&#xff09;常用的包 &#xff08;三&#xff09;如何引入&#xff08;导入&#xff09;包 &#xff08;四&am…
阅读更多...
挑战字节软件测试岗，原来这么轻松...

挑战字节软件测试岗，原来这么轻松...

当前就业环境&#xff0c;裁员、失业消息满天飞&#xff0c;好像有一份工作就不错了&#xff0c;更别说高薪了。其实这只是一方面&#xff0c;而另一方面&#xff0c;各大企业依然求贤若渴&#xff0c;高技术人才依然紧缺&#xff0c;只要你技术过硬&#xff0c;拿个年薪50w不是…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023