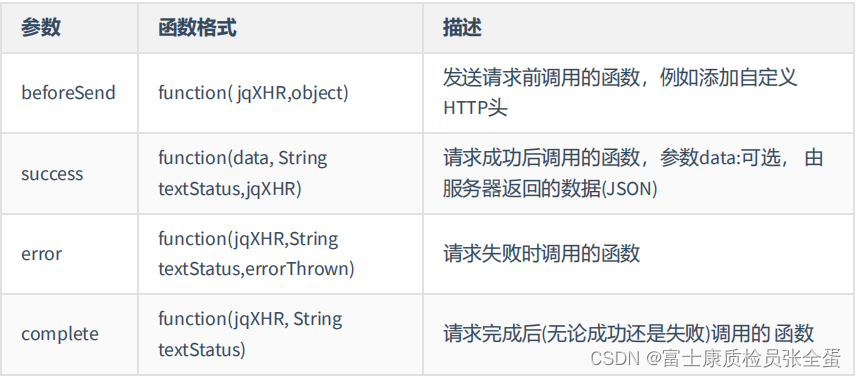
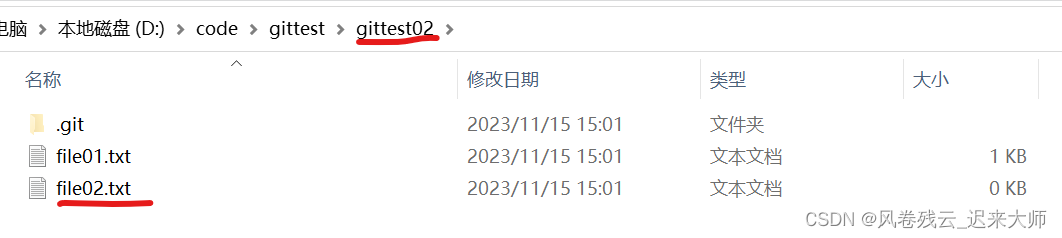
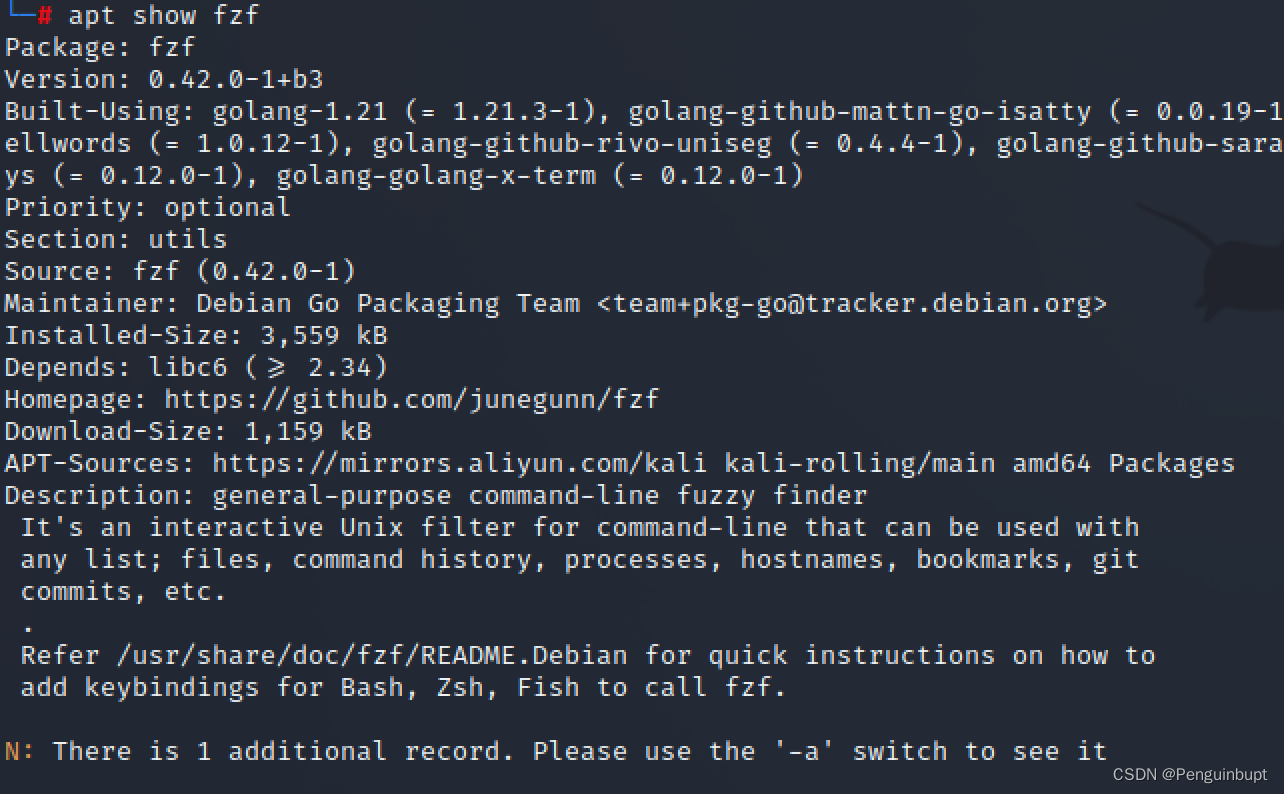
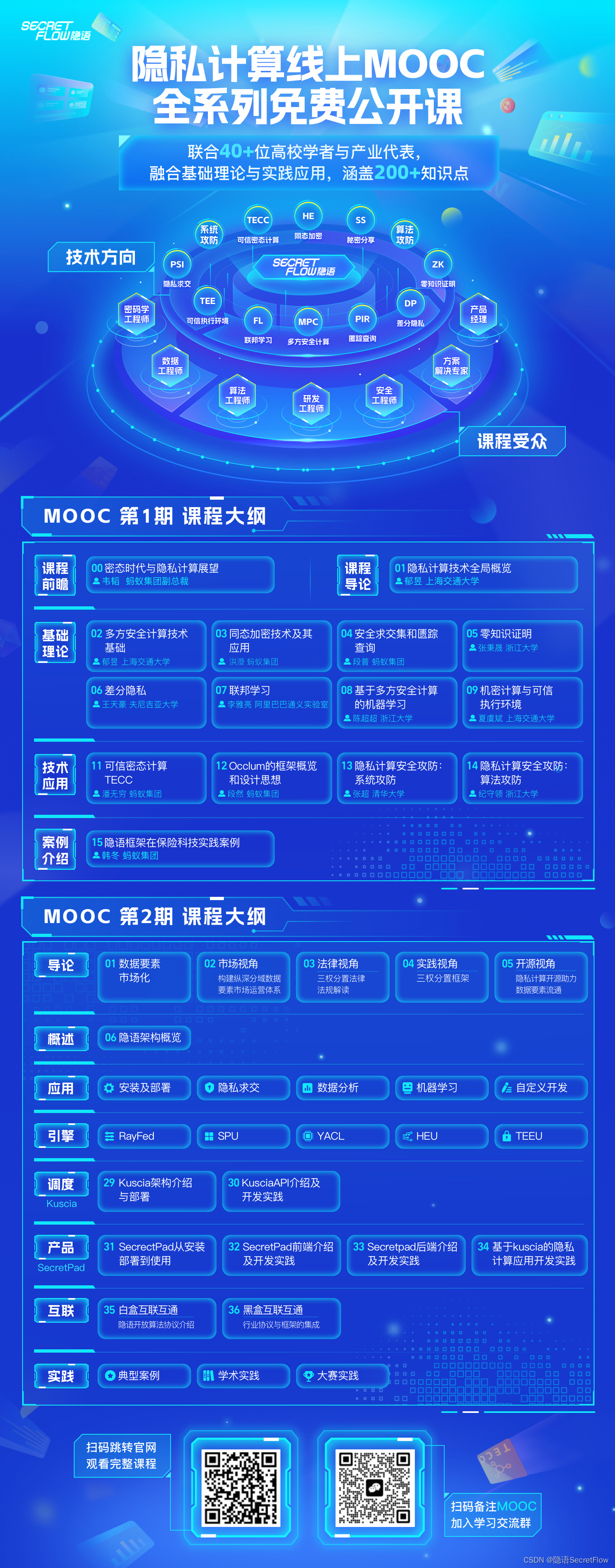
此处为曲线积分------>【问题思考总结】第一型曲线积分和第二型曲线积分的区别与联系【从几何知识的角度思考】

一二型曲面积分有什么区别？（了解）

一型曲面积分： 由dS进行表示。可以想像，dS是一个面积微元，被积函数可以想象成密度，那么这个第一型曲面积分就有物理意义即物质曲面的质量。

-------------------注意：加粗的dxdy，dydz，dzdx代表是有方向的，分正负的。--------------

二型曲线积分：由dxdy，dydz，dzdx进行表示。设F（x，y，z）=P（x，y，z）i+Q（x，y，z）j+R（x，y，z）k（注：（i，j，k）为方向向量，亦可表示为（dxdy，dydz，dzdx））（此处ijk替换为类推，正确性存疑，恳请博友指正）。

其中，P（x，y，z）为xoy面的通量，Q（x，y，z）为yoz面的通量，R（x，y，z）为xoz面的通量，对F（x，y，z）积分可以得到通过某曲面总通量。

两类曲面积分是如何进行转化的？（掌握）

一二型曲面积分的转化如下：


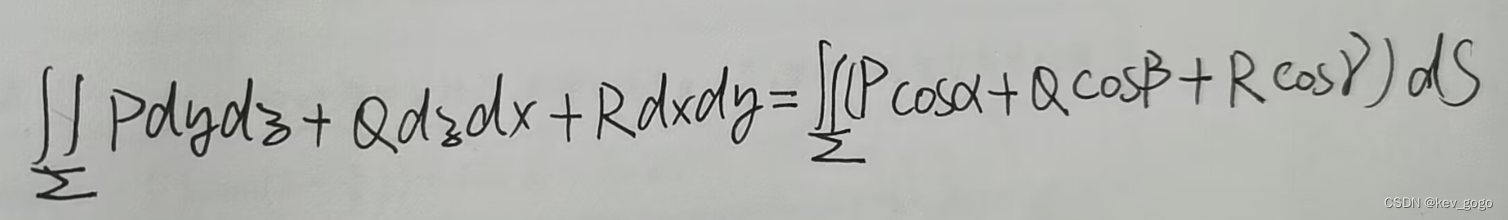
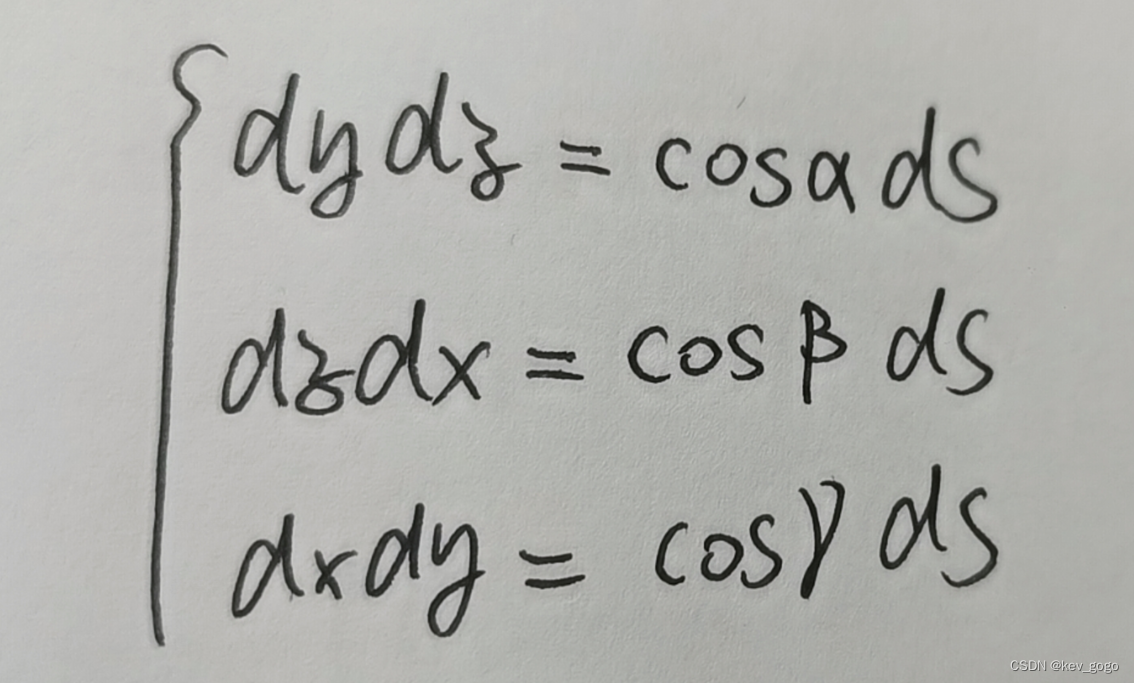
（注：cosα为曲面法向量与x轴的夹角的方向余弦，cosβ为曲面法向量与y轴的夹角的方向余弦，cosγ为曲面法向量与z轴的夹角的方向余弦）
原因可以简单的从以下的角度来理解：

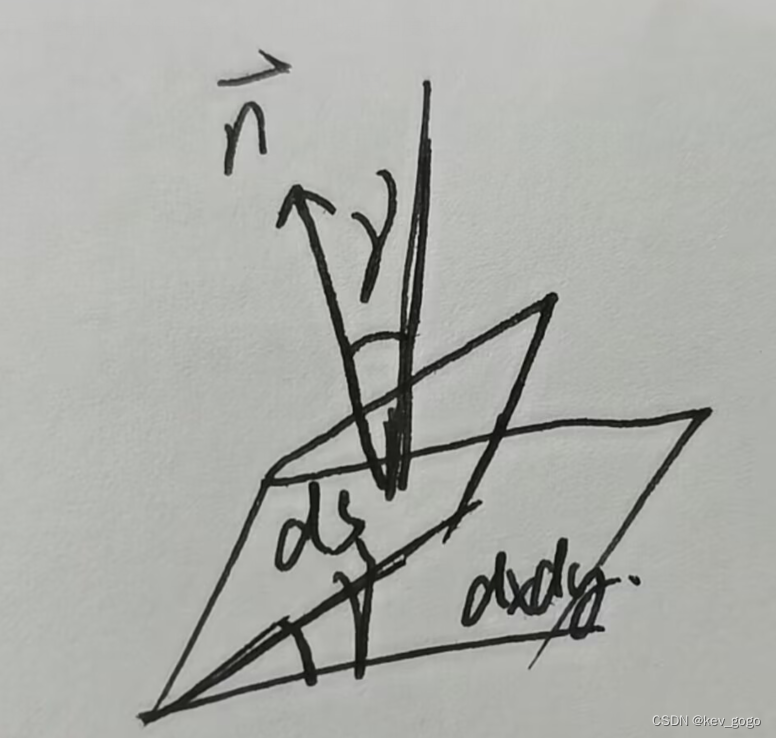
即微分变量之间的投影关系。

其中，有两个我们不那么熟悉的变量需要注意：1. dS 2. cos（Q：为什么dS不带方向呢？A：因为方向隐含在cos中）

首先是dS，其转化如下：

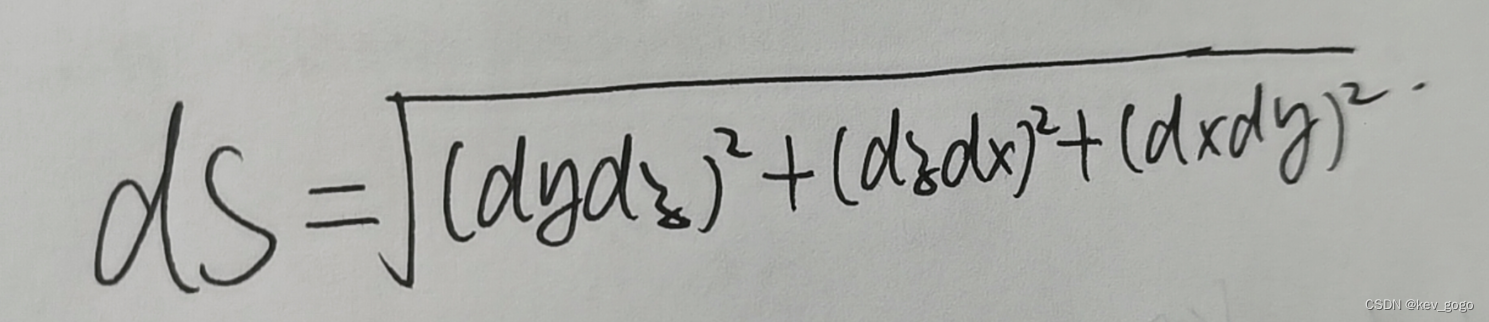
这既可以用几何的角度来想像（通过三维面积勾股定理），也可以用代数的方法来计算（将图二公式两侧均进行平方并相加）。

然后是cos，其转化如下：

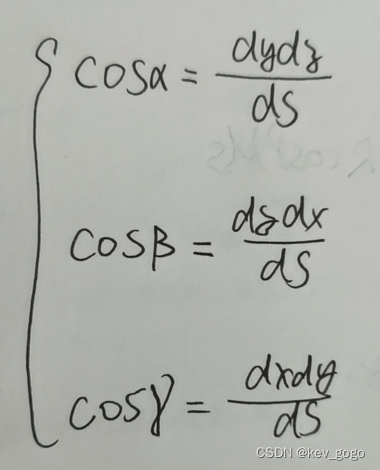
这既可以用几何的角度来想像（通过几何的邻比斜进行想象（我比较喜欢用cosγ进行想象）），也可以用代数的方法来计算（将图二公式两侧除以dS）。

简单应用