1. 题目链接:417. 太平洋大西洋水流问题
2. 题目描述:
有一个
m × n的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。这个岛被分割成一个由若干方形单元格组成的网格。给定一个
m x n的整数矩阵heights,heights[r][c]表示坐标(r, c)上单元格 高于海平面的高度 。岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标
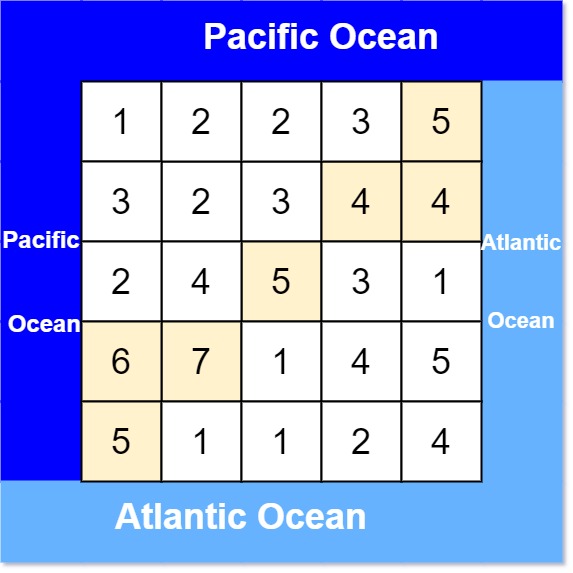
result的 2D 列表 ,其中result[i] = [ri, ci]表示雨水从单元格(ri, ci)流动 既可流向太平洋也可流向大西洋 。示例 1:
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]示例 2:
输入: heights = [[2,1],[1,2]] 输出: [[0,0],[0,1],[1,0],[1,1]]提示:
m == heights.leng thn == heights[r].length1 <= m, n <= 2000 <= heights[r][c] <= 105
3. 解法:
算法思路:
正难则反
如果直接去判断某一个位置是否既能到大西洋也能到太平洋,会重复遍历很多路径
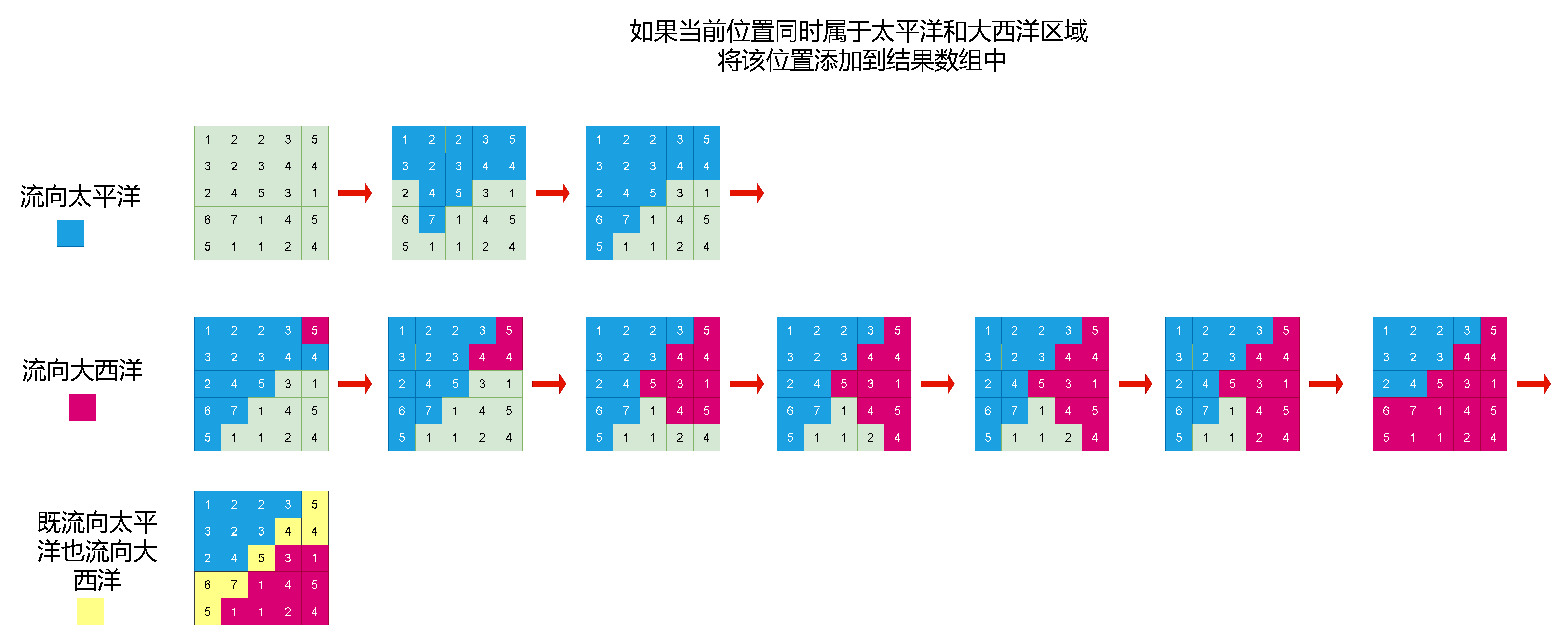
我们反着来,从大西洋沿岸开始反向dfs,这样就能找到哪些点可以流向大西洋;同理,从太平洋沿岸也反向dfs,这样就能找出哪些点可以流向太平洋。那么,被标记两次的点,就是我们要找的结果。
- 定义两个二维布尔数组
pac和atl,分别表示太平洋区域和大西洋区域。 - 从四个边界开始进行深度优先搜索,将可以到达太平洋的区域标记为
true。 - 再次从四个边界开始进行深度优先搜索,将可以到达大西洋的区域标记为
true - 遍历整个矩阵,如果某个单元格同时在
pac和atl中被标记为true,那么就将其添加到结果数组中。
C++算法代码:
class Solution {
int m,n; // 定义两个变量m和n,分别表示矩阵的行数和列数
int dx[4]={0,0,1,-1}; // 定义一个数组dx,表示四个方向的横坐标偏移量
int dy[4]={1,-1,0,0}; // 定义一个数组dy,表示四个方向的纵坐标偏移量
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
m=heights.size(),n=heights[0].size(); // 获取矩阵的行数和列数
vector<vector<bool>> pac(m,vector<bool>(n)); // 定义一个二维布尔数组pac,表示太平洋区域
vector<vector<bool>> atl(m,vector<bool>(n)); // 定义一个二维布尔数组atl,表示大西洋区域
//先处理pac洋
for(int j=0;j<n;j++) dfs(heights,0,j,pac); // 从第一行的每一列开始进行深度优先搜索
for(int i=0;i<m;i++) dfs(heights,i,0,pac); // 从第一列的每一行开始进行深度优先搜索
//处理atl洋
for(int i=0;i<m;i++) dfs(heights,i,n-1,atl); // 从最后一行的每一列开始进行深度优先搜索
for(int j=0;j<n;j++) dfs(heights,m-1,j,atl); // 从最后一列的每一行开始进行深度优先搜索
vector<vector<int>> ret; // 定义一个二维整数数组ret,用于存储最终结果
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(pac[i][j]&&atl[i][j]) // 如果当前位置同时属于太平洋和大西洋区域
{
ret.push_back({i,j}); // 将该位置添加到结果数组中
}
}
}
return ret; // 返回结果数组
}
void dfs(vector<vector<int>>&heights,int i,int j,vector<vector<bool>>& vis) // 定义深度优先搜索函数
{
vis[i][j]=true; // 标记当前位置已访问
for(int k=0;k<4;k++) // 遍历四个方向
{
int x=i+dx[k],y=j+dy[k]; // 计算下一个位置的坐标
if(x>=0 && x<m && y>=0 && y<n && !vis[x][y] && heights[x][y]>=heights[i][j]) // 如果下一个位置在矩阵范围内且未被访问过且高度大于等于当前位置的高度
{
dfs(heights,x,y,vis); // 继续深度优先搜索
}
}
}
};