写在前文
尽管减隔震技术与有限元结合取得了众多成果,但仍面临诸多挑战,如材料非线性、模型不确定性等等。减隔震设计除了常规的宏观结构设计采用SAP2000、Etabs、Midas、SSG、Paco-SAP 或 YJK\PKPM等。
【JY】各类有限元软件计算功能赏析与探讨
我们需要更清楚减隔震元件的破坏模式,对减隔震元件进行破坏分析,除了对减隔震元件在正常工况下的性能进行评估,有限元技术还可以用于研究元件在极端条件下的破坏行为。这有助于了解元件的破坏机理,并为设计提供更全面的数据支撑。
并且在多物理场耦合分析也需要运用在实际应用中,因为减隔震元件可能会面临复杂的物理环境,如温度变化、流体流动等。有限元技术可以考虑这些多物理场耦合效应,从而更准确地预测元件在实际工况下的性能。
黏滞阻尼器的固流耦合分析:
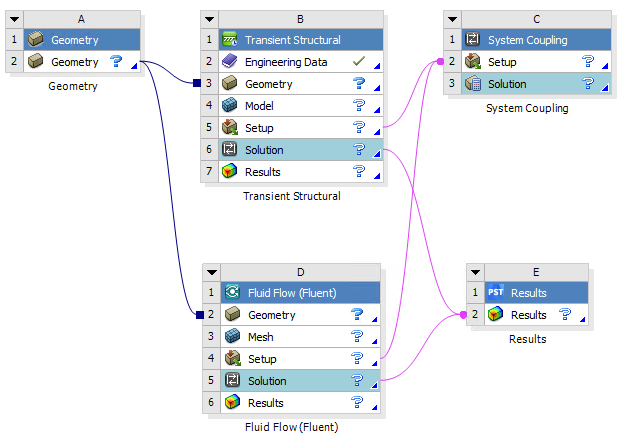
 对于ABAQUS的单元介绍已经做了详尽,个人感觉固体力学上ABAQUS还是上手比较方便,而多场耦合、快速建模预估Workbench会方便一些,因人而异:
对于ABAQUS的单元介绍已经做了详尽,个人感觉固体力学上ABAQUS还是上手比较方便,而多场耦合、快速建模预估Workbench会方便一些,因人而异:
【JY】有限单元分析的常见问题及单元选择
ANSYS Workbench就像一个科技界的“瑞士军刀”,集合了各种强大的单元技术,为减隔震元件提供全面且准确的分析支持。近期对于ANSYS Workbench进行了学习,本文将对ANSYS Workbench 各类单元技术做一个笔记总结,便于为减隔震元件分析提供理论基础。(毕竟Workbench大部分时候会自动匹配相应所需技术)
B-bar方法完全积分
Workbench中的B-bar方法是一种常用于处理低阶单元完全积分的技术,也被称为选择性减积分策略。它是针对有限元分析(FEA)中的一种改进方法,旨在提高计算效率和准确性。
在传统的有限元分析中,低阶单元(如线性单元)在处理不可压缩材料或近似不可压缩材料时,常常遇到体积锁定问题。体积锁定是指在近似不可压缩材料的有限元模拟中,由于体积应变被过度限制,导致计算结果偏离实际情况的现象。为了解决这个问题,B-bar方法被引入到ANSYS Workbench中。
B-bar方法的核心思想是在低阶单元的完全积分过程中进行选择性减积分。它通过将高斯积分点处的体积应变替换为单元的平均体积应变,实现了对应变的软化处理,从而防止了体积锁定的发生。这种选择性减积分的策略可以在保证计算精度的同时,提高计算的收敛性和效率。
需要注意的是,B-bar方法并不能解决剪切锁定问题,这是另一种常见的有限元分析问题。对于弯曲主导的问题,剪切锁定可能导致结果的失真。因此,在处理这类问题时,用户需要采用其他方法,如使用增强应变公式等。
它通过选择性减积分策略,防止了体积锁定的发生,提高了计算的准确性和效率。然而,对于剪切锁定等问题,仍需结合其他方法进行解决。该技术也可与混合U-P一起使用。
B-bar方法(完全积分)主要应用在需要更高精度和可靠性的有限元分析中。以下是几种典型的应用情况:
需要精确模拟体积应变的问题:B-bar方法通过完全积分计算体积应变,能够更准确地模拟和分析材料的变形行为,特别适用于处理不可压缩或近似不可压缩材料的问题。
弯曲主导的问题:完全积分的B-bar方法可以有效地处理弯曲主导的问题,其中剪切锁定的影响较小。它可以提供更稳定和准确的结果,避免剪切锁定引起的误差。
复杂应力状态分析:对于复杂应力状态下的结构分析,完全积分的B-bar方法具有更高的精度和可靠性。它能够更好地捕捉应力分布的细微特征,并提供更准确的结果。
缩减积分
Workbench中的缩减积分,也被称为统一缩减积分,是一种针对高阶(二阶)单元的默认积分策略。在这种方法中,体积项和偏差项均采用了简化积分的处理方式。缩减积分方法在多个方面具有优势。
首先,它有助于防止在弯曲主导的问题中出现的剪切锁定现象。
其次,当处理接近不可压缩的材料时,它也有助于避免体积锁定问题。
对于低阶单元,经过缩减积分处理后,仅有一个积分点,这使得该选项在计算效率上超越了B-bar方法(选择性减积分)和增强应变公式。
然而,需要注意的是,使用这种方法可能会出现沙漏现象。
【沙漏现象】又称为零能量模式,特指在采用单一积分点的低阶四边形或六面体单元中,出现的一种特定行为。在这种模式下,当单元发生弯曲变形时,通过积分点的水平线与竖直线的长度并不会发生变化,且其夹角也保持恒定。由此导致的结果是,这个积分点并未获得任何单元应变能。这也意味着,在这一点,所有的应力分量都为零。因此,这样的单元不具备刚度,也就无法对抗任何形式的变形,使得导致计算结果的失真。
与低阶单元不同,由于二次形函数的使用,高阶单元本身不具有剪切锁定的问题。
但是,如果使用了完全积分方案,高阶单元可能会发生体积锁定。为了避免这一问题,高阶单元在Workbench中默认或唯一采用的便是统一降积分的策略。这样的选择确保了高阶单元在处理复杂问题时的准确性和稳定性,同时也提高了计算效率。该技术也可与混合U-P一起使用。
缩减积分技术一般在以下情况中应用:
大规模有限元分析:当模型的规模和复杂度很高时,传统的有限元分析方法可能会消耗大量的计算资源。缩减积分技术可以在保证一定精度的前提下,减少计算量,提高分析的效率。
有限计算资源的情况:当计算资源有限时,比如使用个人电脑或小型服务器进行模拟,缩减积分技术能够以更少的计算资源得出相对合理的结果。
对分析时间有要求的情况:在某些项目中,时间是一个关键因素。缩减积分技术可以加速有限元分析的过程,从而更快地得到分析结果。
初步设计和快速评估:在产品的初步设计阶段,工程师可能需要快速评估多个设计方案。缩减积分技术可以为这些初步评估提供相对准确的结果,而不需要完整的精细模拟。
非协调模式
非协调模式也称增强应变,是一种特殊的应变计算方法。它特别设计用来防止在弯曲主导的问题中的剪切锁定,以及接近不可压缩情况下的体积锁定。为了实现这一目标,增强应变公式引入了一定数量的内部自由度。
它们的存在完全是为了克服剪切锁定问题。对于体积锁定,该方法也引入了附加的内部自由度。不过,二维单元中的平面应力情况是个例外。
值得注意的是,这些所有的内部自由度都是在单元级别自动引入的,无需用户手动干预。这也意味着,当使用增强应变公式时,单元的质量变得尤为重要。单元质量越好,计算精度自然也会越高。
不过,也由于其额外的计算开销和复杂性,增强应变公式的计算效率低于B方法(选择性减少积分)或者均匀减少积分选项。所以在选择使用增强应变公式时,需要权衡其精度和效率之间的取舍。该技术也可与混合U-P一起使用。
增强应变技术一般在以下几种情况中应用:
处理剪切锁定问题:当模型存在弯曲主导的问题时,剪切锁定可能会成为一个难题。这时,增强应变技术可以用来有效地防止剪切锁定,提高计算的准确性。
处理体积锁定问题:当分析的材料接近不可压缩状态时,体积锁定现象可能会发生。增强应变技术能够用来解决这类体积锁定问题。
需要高精度应变计算的情况:如果分析中对应变的计算精度要求较高,增强应变技术可以通过引入内部自由度来提高计算精度,从而更准确地预测应变分布。
简化的增强应变
Workbench的简化的增强应变技术是一种专门设计的技术,对于剪切锁定相关的问题尤其有效。
该技术具有简化的特点,同时融入了增强应变的元素。在防止弯曲主导问题中的剪切锁定方面,简化的增强应变技术非常有效。与其他的增强应变技术相比,它的独特之处在于仅引入防止剪切锁定所需的内部自由度,而没有引入额外的计算复杂度。这使得该技术能在保证计算精度的前提下,提高计算效率。
对于平面应力状态,简化的增强应变公式与标准的增强应变公式相同,能够提供稳定和准确的结果。
然而,需要注意的是,由于没有内部自由度来处理体积锁定,当材料接近不可压缩状态时,该技术可能并不理想。这意味着,对于接近不可压缩材料的体积自锁问题,简化的增强应变技术可能无法提供有效的解决方案。
在实际应用中,该技术经常与混合U-P方法一起使用。这种结合使用的方式可以进一步提高有限元分析的准确性和效率,扩大该技术的应用范围。
Workbench的简化的增强应变技术提供了一种平衡精度和效率的解决方案,尤其适用于需要解决剪切锁定问题,同时对计算时间和资源有要求的情况。但在处理接近不可压缩材料的问题时,可能需要考虑其他技术或策略。
简化的增强应变技术一般应用在需要快速、有效地模拟和分析剪切主导的问题的情况下。特别是当模型的剪切变形是主要的关注点,并且需要避免剪切锁定现象时,这种技术是非常有用的。
简化的增强应变技术与(非协调模式)增强应变技术的主要区别体现在以下几个方面:
内部自由度的引入:简化的增强应变技术仅引入防止剪切锁定所需的内部自由度,而其他的增强应变技术可能会引入更多的内部自由度来解决其他问题,比如体积锁定。因此,简化的增强应变技术在内部自由度的使用上更为精简。
计算效率和资源消耗:由于简化的增强应变技术仅引入必要的内部自由度,它通常具有更高的计算效率,并减少计算资源的消耗。相比之下,其他的增强应变技术可能需要更多的计算资源和时间来处理额外的内部自由度。
对体积锁定的处理:简化的增强应变技术没有内部自由度来处理体积锁定问题。因此,当材料接近不可压缩时,该技术可能无法有效处理体积自锁问题。而其他一些增强应变技术可能通过引入处理体积锁定的内部自由度来应对这种情况。
混合U-P ⭐⭐⭐
Workbench的混合U-P是一种结合了U(位移)和P(压力)的自由度来处理有限元分析中的某些特定问题的方法。
在有限元分析中,处理那些涉及不可压缩或接近不可压缩材料的问题时,常常会遇到体积锁定现象。这种现象可能导致计算结果的失真和不准确。为了解决这个问题,采用混合U-P方法是一种强大而有效的工具,用于解决有限元分析中的体积锁定问题,特别是涉及不可压缩或接近不可压缩材料的情况。
该方法的核心思想是通过同时使用位移(U)和压力(P)作为自由度来进行模拟。这种混合的方式能够有效地解决体积锁定问题,并提供更准确和稳定的计算结果。
混合U-P方法在处理不可压缩材料问题时特别有效,因为它能够同时考虑材料的变形和体积变化。通过引入适当的内部自由度和公式,该方法能够更精确地模拟材料的响应,并减少计算误差。
混合U-P可较好的模拟橡胶材料本构,例如 Mooney-Rivlin、Neo-Hookean、Ogden、Arruda-Boyce、多项式形式和用户定义模型。
对于混合U-P技术,一般在以下几种情况中应用:
处理不可压缩材料问题:当分析涉及不可压缩材料时,混合U-P技术能够更准确地模拟材料的变形行为,帮助解决体积锁定问题。
解决体积锁定现象:体积锁定现象可能导致计算结果的失真和不准确,混合U-P技术通过同时考虑位移和压力自由度,有效地消除了体积锁定,提高了计算精度。
要求高精度模拟:当分析中需要高精度地模拟结构的变形和应力分布时,混合U-P技术提供了更精确和可靠的结果,满足对计算精度要求较高的情况。
复杂模型分析:对于复杂的有限元模型,特别是涉及大变形、接触和非线性材料行为等问题,混合U-P技术能够更好地处理这些挑战,提供稳定和准确的解决方案。
注意:通常开启混合U-P技术时,应打开大挠度变形。

总结
在有限元分析中,为了应对各种复杂的问题和提高计算效率与精度,Workbench提供了多种方法,其中包括B-bar方法完全积分、缩减积分、非协调模式、简化的增强应变以及混合U-P等。这些方法各有优缺点,适用于不同的问题场景。
B-bar方法完全积分:这是一种高精度的方法,适用于需要精确模拟体积应变和复杂应力状态的问题。它能提供更稳定和准确的结果,但也可能增加计算的复杂性和资源需求。
缩减积分:这种方法在提高计算效率的同时,牺牲了一部分计算精度。它特别适用于大规模有限元分析和有限计算资源的情况,能够加速分析过程。
非协调模式:非协调模式在处理某些特定问题时具有优势,它能够克服某些协调模式中的局限性,但也可能引入额外的复杂性和难度。
简化的增强应变:这种方法通过仅引入防止剪切锁定所需的内部自由度来平衡计算精度和效率。它适用于需要快速有效地模拟剪切主导的问题,并避免剪切锁定的情况。
混合U-P:混合U-P方法通过结合位移和压力自由度来解决体积锁定问题,特别是涉及不可压缩或接近不可压缩材料的情况。它提供了更高的计算精度和可靠性。
概念为先,机理为本!
完
更多精彩,关注建源学堂!
【往期精彩】
# 性能分析
【JY】基于性能的抗震设计浅析(一)
【JY】基于性能的抗震设计浅析(二)
【JY】浅析消能附加阻尼比
【JY】近断层结构设计策略分析与讨论
【JY】浅析各动力求解算法及其算法数值阻尼(人工阻尼)理念
【JY|体系】结构概念设计之(结构体系概念)
【JY|理念】结构概念设计之(设计理念进展)
【JY|减震】结构概念之(消能减震黏滞阻尼器)
【JY|隔震】结构概念设计之(隔震概念设计)
【JY】有限单元分析的常见问题及单元选择
【JY】结构动力学之显隐式
【JY】浅谈结构设计
【JY】浅谈混凝土损伤模型及Abaqus中CDP的应用
【JY】浅谈混凝土结构/构件性能试验指标概念(一)
【JY】浅谈混凝土结构/构件性能试验指标概念(二)
【JY】橡胶系支座/摩擦系支座全面解析
【JY】《公路桥梁抗震性能评价细则》宣贯PPT
【JY】减隔震设计思考:隔震篇
【JY】浅析基于性能的抗震分析方法——性能设计
【JY】这个房子应该做抗震or减隔震?
【JY】减隔震设计思考Ⅱ
# 概念机理
【JY】基于Ramberg-Osgood本构模型的双线性计算分析
【JY】结构动力学初步-单质点结构的瞬态动力学分析
【JY】从一根悬臂梁说起
【JY】反应谱的详解与介绍
【JY】结构瑞利阻尼与经济订货模型
【JY】主成分分析与振型分解
【JY】浅谈结构多点激励之概念机理(上)
【JY】浅谈结构多点激励之分析方法(下)
【JY】板壳单元的分析详解
【JY】橡胶支座的简述和其力学性能计算
【JY】振型求解之子空间迭代
【JY】橡胶支座精细化模拟与有限元分析注意要点
【JY】推开土木工程振型求解之兰索斯法(Lanczos法)的大门
【JY】基于OpenSees和Sap2000静力动力计算案例分析
【JY】建筑结构施加地震波的方法与理论机理
【JY】力荐佳作《结构地震分析编程与应用》
【JY】ABAQUS子程序UEL的有限元原理与应用
【JY】钢筋混凝土正截面极限承载力设计的基本原理和快速计算方法
【JY】消能减震黏滞阻尼器的力学原理与应用
【JY】力荐 | 区域建筑地震安全性有限元分析示例
【JY】ABAQUS正交各向异性弹性本构模型
【JY】求?减隔震元件的滞回面积~
# 软件讨论
【JY】模态分析关键点笔记
【JY】各软件框架的弹塑性分析对比
【JY】浅析时程分析中的阻尼设置
【JY】减隔震元件计算表格分享
【JY】复合材料分析利器—内聚力单元
【JY】SDOF计算教学软件开发应用分享
【JY】Abaqus6.14-4如何关联fortran?
【JY】如何利用python来编写GUI?
【JY】如何解决MATLAB GUI编程软件移植运行问题?
【JY】浅谈结构分析与设计软件
【JY|STR】求解器之三维结构振型分析
【JY】SignalData软件开发应用分享
【JY】基于Matlab的双线性滞回代码编写教程
【JY】动力学利器 —— JYdyn函数包分享与体验
【JY】混凝土分析工具箱:CDP模型插件与滞回曲线数据
【JY】结构工程分析软件讨论(上)
【JY】结构工程分析软件讨论(下)
【JY】各类有限元软件计算功能赏析与探讨
【JY】ETABS与Perform3D弹塑性分析功能对比示例
【JY】自建9000条高质量人工波可供下载
【JY】代码|极简反应谱分析
#其他
【JY】位移角还是有害位移角?
【JY】如何利用python来编写GUI?
【JY】今日科普之BIM