【数据结构】树与二叉树（十五）：二叉树的基础操作：查找结点（算法Find）

文章目录

5.2.1 二叉树
- 二叉树性质
- 满二叉树、完全二叉树定义、特点及相关证明
5.2.2 二叉树顺序存储
5.2.3 二叉树链接存储
5.2.4 二叉树的遍历
- 1-3 先序、中序、后序遍历递归实现及相关练习
- 4. 中序遍历非递归
- 5. 后序遍历非递归
- 6. 先序遍历非递归
- 7. 层次遍历
5.2.5 二叉树的创建
- 1. 先序创建
- 2. 复制二叉树
5.2.6 二叉树的基础操作
- 1. 查找给定结点的父亲
- 2. 查找结点
- - a. 算法Find
  - b. 时间复杂度
  - c. 代码实现
  - d. 递归流程
  - e. 算法测试
- 3. 代码整合

5.2.1 二叉树

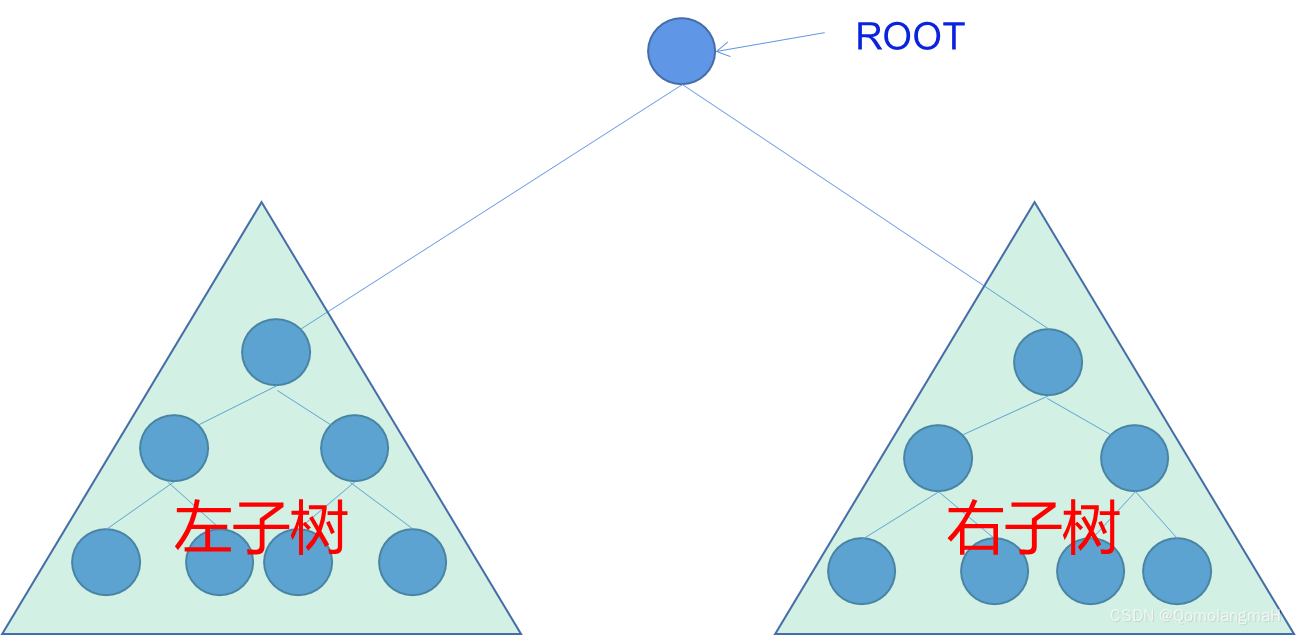
二叉树是一种常见的树状数据结构，它由结点的有限集合组成。一个二叉树要么是空集，被称为空二叉树，要么由一个根结点和两棵不相交的子树组成，分别称为左子树和右子树。每个结点最多有两个子结点，分别称为左子结点和右子结点。
在这里插入图片描述

二叉树性质

引理5.1：二叉树中层数为i的结点至多有 $2^i$ 个，其中 $\geq 0$ 。

引理5.2：高度为k的二叉树中至多有 $2^{k+1}-1$ 个结点，其中 $\geq 0$ 。

引理5.3：设T是由n个结点构成的二叉树，其中叶结点个数为 $n_0$ ，度数为2的结点个数为 $n_2$ ，则有 $n_0 = n_2 + 1$ 。

详细证明过程见前文：【数据结构】树与二叉树（三）：二叉树的定义、特点、性质及相关证明

满二叉树、完全二叉树定义、特点及相关证明

详细证明过程见前文：【数据结构】树与二叉树（四）：满二叉树、完全二叉树及其性质

5.2.2 二叉树顺序存储

二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中，详见：
【数据结构】树与二叉树（五）：二叉树的顺序存储（初始化，插入结点，获取父节点、左右子节点等）

5.2.3 二叉树链接存储

二叉树的链接存储系指二叉树诸结点被随机存放在内存空间中，结点之间的关系用指针说明。在链式存储中，每个二叉树结点都包含三个域：数据域（Data）、左指针域（Left）和右指针域（Right），用于存储结点的信息和指向子结点的指针，详见：
【数据结构】树与二叉树（六）：二叉树的链式存储

5.2.4 二叉树的遍历

遍历（Traversal）是对二叉树中所有节点按照一定顺序进行访问的过程。
通过遍历，可以访问树中的每个节点，并按照特定的顺序对它们进行处理。
对二叉树的一次完整遍历，可给出树中结点的一种线性排序。
- 在二叉树中，常用的遍历方式有三种：先序遍历、中序遍历和后序遍历。
- 这三种遍历方式都可以递归地进行，它们的区别在于节点的访问顺序。
  - 在实现遍历算法时，需要考虑递归终止条件和递归调用的顺序。
- 还可以使用迭代的方式来实现遍历算法，使用栈或队列等数据结构来辅助实现。
遍历是二叉树中基础而重要的操作，它为其他许多操作提供了基础，如搜索、插入、删除等。

1-3 先序、中序、后序遍历递归实现及相关练习

【数据结构】树与二叉树（七）：二叉树的遍历（先序、中序、后序及其C语言实现）

4. 中序遍历非递归

【数据结构】树与二叉树（八）：二叉树的中序遍历（非递归算法NIO）

5. 后序遍历非递归

【数据结构】树与二叉树（九）：二叉树的后序遍历（非递归算法NPO）

6. 先序遍历非递归

【数据结构】树与二叉树（十）：二叉树的先序遍历（非递归算法NPO）

7. 层次遍历

【数据结构】树与二叉树（十一）：二叉树的层次遍历（算法LevelOrder）

5.2.5 二叉树的创建

1. 先序创建

由二叉树的遍历，很容易想到用遍历方法去创建二叉树，我们考虑从先根遍历思想出发来构造二叉树：

【数据结构】树与二叉树（十二）：二叉树的递归创建（算法CBT）

2. 复制二叉树

考虑用后根遍历思想递归复制二叉树的算法CopyTree：

【数据结构】树与二叉树（十三）：递归复制二叉树（算法CopyTree）

5.2.6 二叉树的基础操作

1. 查找给定结点的父亲

递归思想
- 给定结点是指给定的是一个指向某个结点的指针(比如p)。
- 返回值也应该是指针，指向结点p之父亲的指针（找不到时为空）。

【数据结构】树与二叉树（十四）：二叉树的基础操作：查找给定结点的父亲（算法Father ）

2. 查找结点

考虑利用先根遍历在二叉树中搜索符合数据条件(item)的结点p，即满足data§=item的结点。
在这里插入图片描述

a. 算法Find

在这里插入图片描述

b. 时间复杂度

在Find算法中，每个节点最多需要进行一次比较操作。在最坏的情况下，需要比较的节点数等于二叉树的节点总数 n。因此，算法 Find 的时间复杂度是 O(n)，其中 n 是二叉树的节点数。

在最坏情况下，算法的运行时间与二叉树中的节点数量成正比。
在实际应用中，这种算法的效率可能取决于树的形状，因为不同的树结构可能导致算法的性能有所不同。

c. 代码实现

struct Node* findNode(struct Node* root, char item) {
    if (root == NULL) {
        return NULL;
    }

    if (root->data == item) {
        return root;
    }

    struct Node* leftResult = findNode(root->left, item);
    if (leftResult != NULL) {
        return leftResult;
    }

    return findNode(root->right, item);
}

d. 递归流程

如果树为空，则返回NULL
如果当前结点的数据等于item，返回当前结点
在左子树中递归搜索
- 左子树为空，则返回NULL
- 如果当前结点的数据等于item，返回当前结点
- 在左子树的左子树中递归搜索
  - …………
- 在右子树的右子树中递归搜索
  - …………
在右子树中递归搜索
- …………

e. 算法测试

int main() {
    char tostop = '#';
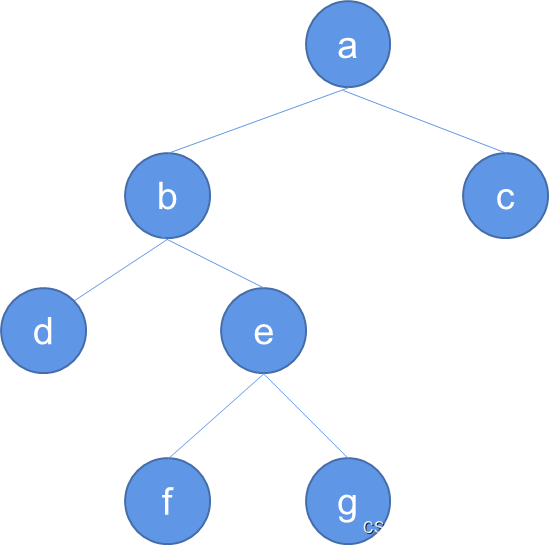
    char input_data[] = {'a', 'b', 'd', '#', '#', 'e', 'f', '#', '#', 'g', '#', '#', 'c', '#', '#'};
    int index = 0;

    struct Node* root = CBT(input_data, &index, tostop);

    char targetItem = 'e';
    struct Node* foundNode = findNode(root, targetItem);

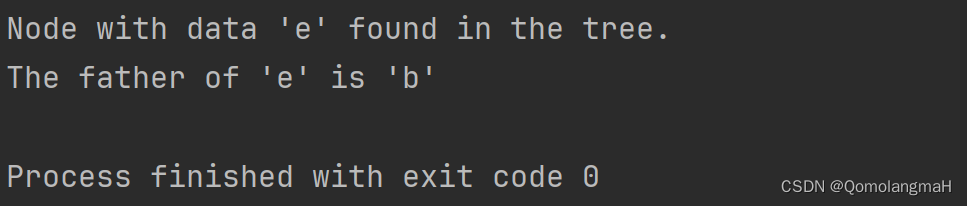
    if (foundNode != NULL) {
        printf("Node with data '%c' found in the tree.\n", targetItem);
    } else {
        printf("Node with data '%c' not found in the tree.\n", targetItem);
    }
    struct Node* fatherNode = findFather(root, foundNode);

    // 输出结果
    if (fatherNode != NULL) {
        printf("The father of '%c' is '%c'\n", foundNode->data, fatherNode->data);
    } else {
        printf("'%c' is either the root or not found in the tree.\n", foundNode->data);
    }
    releaseTree(root);
    root = NULL;

    return 0;
}

采用前文算法CBT，先序递归创建一棵二叉树
调用查找函数查找具有特定数据值的结点，比如找 ‘e’
输出查找结果
调用函数查找该结点的父亲结点
释放整棵树
- 注意，需要将释放的指针置为 NULL，以防止悬空指针

3. 代码整合

#include <stdio.h>
#include <stdlib.h>

struct Node {
    char data;
    struct Node* left;
    struct Node* right;
};

struct Node* createNode(char data) {
    struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
    if (newNode == NULL) {
        printf("Memory allocation failed!\n");
        exit(1);
    }
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

struct Node* CBT(char data[], int* index, char tostop) {
    char ch = data[(*index)++];
    if (ch == tostop) {
        return NULL;
    } else {
        struct Node* t = createNode(ch);
        t->left = CBT(data, index, tostop);
        t->right = CBT(data, index, tostop);
        return t;
    }
}

// 释放以p指向结点为根的树
void releaseTree(struct Node* p) {
    // 如果p为空，则返回
    if (p == NULL) {
        return;
    }

    // 递归释放左子树
    releaseTree(p->left);

    // 递归释放右子树
    releaseTree(p->right);

    // 释放当前节点
    free(p);
}
// 查找给定结点的父亲节点（递归实现）
struct Node* findFather(struct Node* root, struct Node* p) {
    // 如果树为空或者给定结点为空，则返回NULL
    if (root == NULL || p == NULL) {
        return NULL;
    }

    // 如果给定结点是根节点，则根据定义返回NULL
    if (root == p) {
        return NULL;
    }

    // 如果给定结点是根节点的左孩子或右孩子，则根节点就是其父亲
    if (root->left == p || root->right == p) {
        return root;
    }

    // 在左子树中递归查找
    struct Node* leftResult = findFather(root->left, p);
    if (leftResult != NULL) {
        return leftResult;
    }

    // 在右子树中递归查找
    return findFather(root->right, p);
}

// 在二叉树中搜索具有特定数据值的结点
struct Node* findNode(struct Node* root, char item) {
    // 如果树为空，则返回NULL
    if (root == NULL) {
        return NULL;
    }

    // 如果当前结点的数据等于item，返回当前结点
    if (root->data == item) {
        return root;
    }

    // 在左子树中递归搜索
    struct Node* leftResult = findNode(root->left, item);
    if (leftResult != NULL) {
        return leftResult;
    }

    // 在右子树中递归搜索
    return findNode(root->right, item);
}

int main() {
    // 创建一棵二叉树
    char tostop = '#';
    char input_data[] = {'a', 'b', 'd', '#', '#', 'e', 'f', '#', '#', 'g', '#', '#', 'c', '#', '#'};
    int index = 0;

    struct Node* root = CBT(input_data, &index, tostop);


    // 查找具有特定数据值的结点，比如找 'e'
    char targetItem = 'e';
    struct Node* foundNode = findNode(root, targetItem);

    // 输出结果
    if (foundNode != NULL) {
        printf("Node with data '%c' found in the tree.\n", targetItem);
    } else {
        printf("Node with data '%c' not found in the tree.\n", targetItem);
    }
    // 调用函数查找父亲节点
    struct Node* fatherNode = findFather(root, foundNode);

    // 输出结果
    if (fatherNode != NULL) {
        printf("The father of '%c' is '%c'\n", foundNode->data, fatherNode->data);
    } else {
        printf("'%c' is either the root or not found in the tree.\n", foundNode->data);
    }
    releaseTree(root);
    root = NULL;

    return 0;
}