AVL树的插入和删除

news2024/10/6 8:29:57

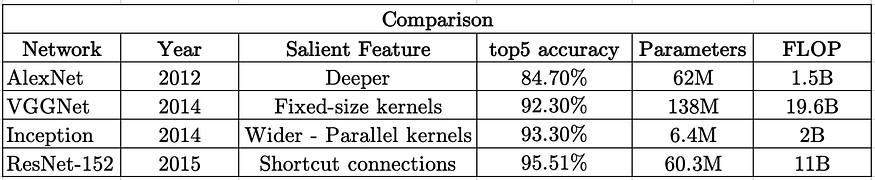
一.AVL树的四种旋转方式

 

 

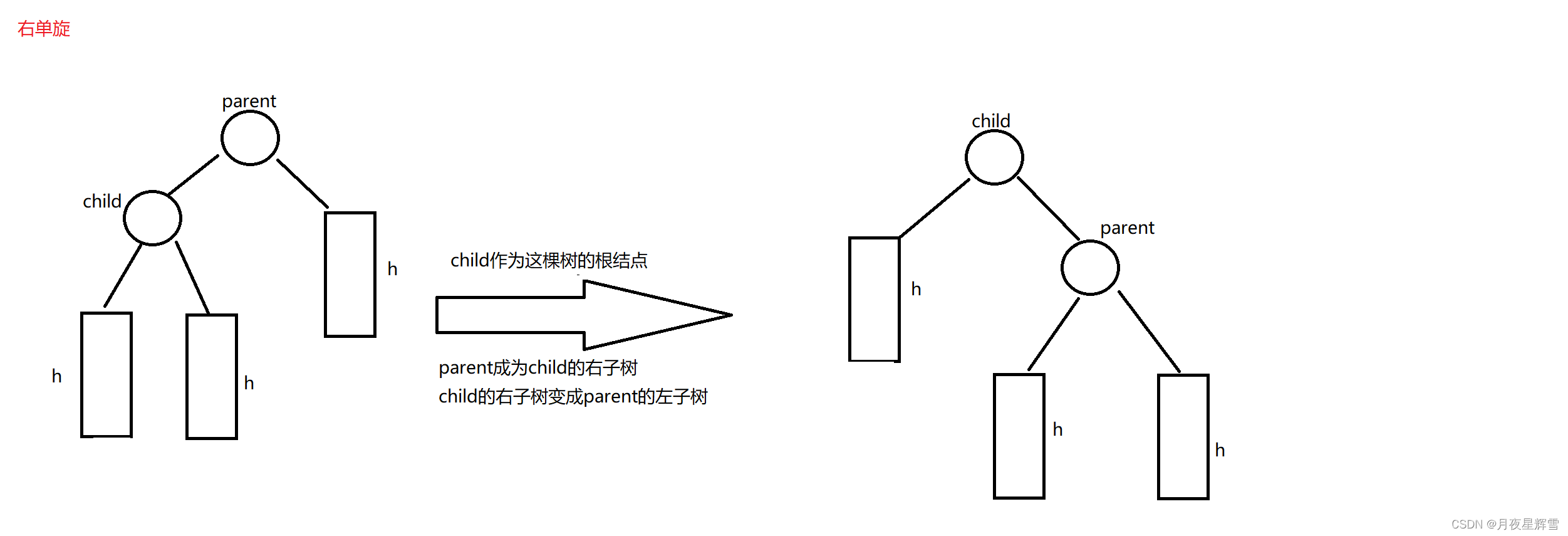
以上是AVL树插入和删除时需要用到的四种旋转方式。为什么要旋转？因为树不平衡了,通过旋转使其再次平衡。 但是上面的四副图在旋转前就是平衡的，所以这样的旋转是没有意义的，重点在于理解旋转的方法。下面的插入和删除操作会用到这四种方法，都是在这四副图的基础上变化。

具体如何选择旋转方法呢？记住以下几个技巧：

  1. 当某个结点(parent)的平衡因子绝对值大于1时(即2或-2)时，需要进行旋转
  2. child永远指向parent高的那颗子树
  3. parent和child都是左边高时右单旋，都是右边高时左单旋
  4. child左边高，parent右边高时进行右左单旋；child右边高，parent左边高时进行左右单旋
  5. 当进行插入和删除操作后，只可能影响被操作结点到根的路径上的所有结点的平衡因子，其余结点不受影响。
  6. 一个结点的平衡因子是否会受到影响，关键看它的子树高度是否发生变化。

二.AVL树的插入操作

parent和child都是左边高，右单旋，插入前和旋转后，这颗树的高度不变(h+1)，故旋转后不用向上更新平衡因子

 parent和child都是右边高，左单旋，插入前和旋转后，这颗树的高度不变(h+1)，故旋转后不用向上更新平衡因子

 parent右边高，child左边高，右左单旋，插入前和旋转后，这颗树的高度不变(h+2)，故旋转后不用向上更新平衡因子

 parent左高，child右边高，左右单旋，插入前和旋转后，这颗树的高度不变(h+2)，故旋转后不用向上更新平衡因子

三.AVL树的删除操作

 parent左边高，child两边一样高，右单旋。插入前和旋转后，这棵树的高度不变(h+2)，故旋转后不用向上更新平衡因子

parent和child都是左边高，右单旋。插入前和旋转后，这棵树的高度发生变化(h+2->h+1)，故旋转后需要向上更新平衡因子

parent右边高，child两边一样高，左单旋。插入前和旋转后，这棵树的高度不变(h+2)，故旋转后需要向上更新平衡因子

parent和child都是右边高，左单旋。插入前和旋转后，这棵树的高度发生变化(h+2->h+1)，故旋转后需要向上更新平衡因子

 parent左边高，child右边高，左右双旋。插入前和旋转后，这棵树的高度发生变化(h+2->h+1)，故旋转后需要向上更新平衡因子

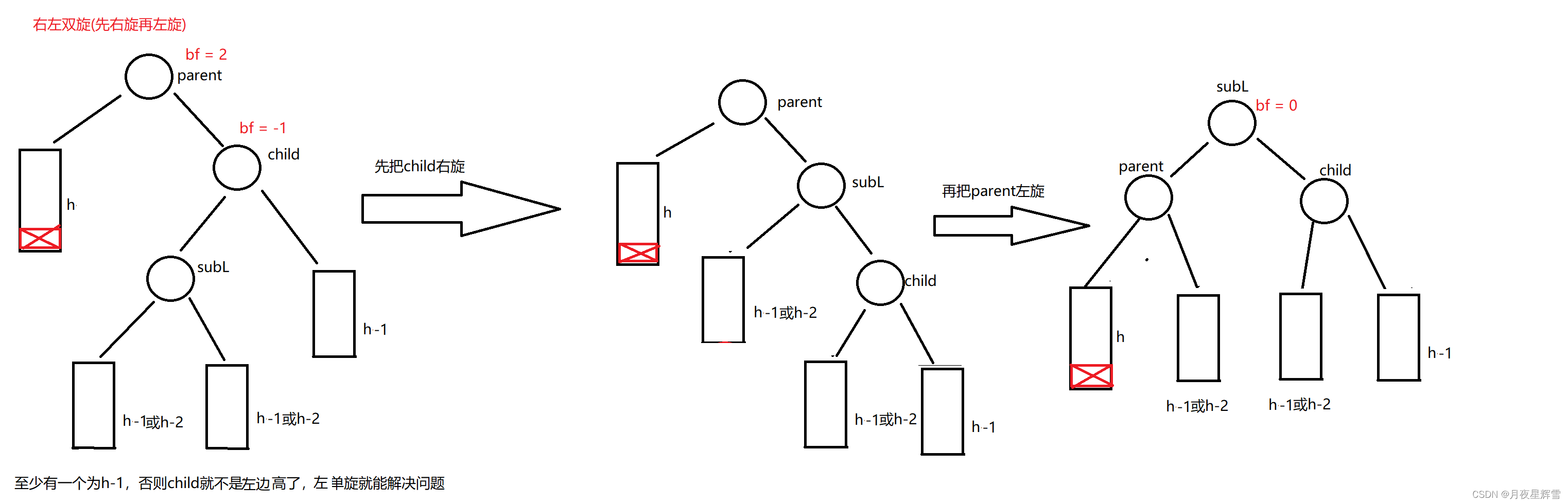 parent右边高，child左边高，右左双旋。插入前和旋转后，这棵树的高度发生变化(h+2->h+1)，故旋转后需要向上更新平衡因子

四.参考代码 

#pragma once
#include <iostream>
#include <assert.h>
using namespace std;

template <class K, class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_bf(0)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{}
	
	pair<K, V> _kv;
	int _bf = 0;//平衡因子
	AVLTreeNode* _left = nullptr;
	AVLTreeNode* _right = nullptr;
	AVLTreeNode* _parent = nullptr;
};

template <class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	AVLTree() = default;
	
	//查找
	Node* find(const K& key)
	{
		Node* cur = _root;
		
		while (cur)
		{
			if (cur->_kv.first == key)
			{
				return cur;
			}
			else if (key > cur->_kv.first)
			{
				cur = cur->_right;
			}
			else
			{
				cur = cur->_left;
			}
		}
		return nullptr;
	}

	//插入
	bool insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			//printf("插入根结点%d\n", kv.first);
			_root = new Node(kv);
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_kv == kv)
			{
				return false;
			}
			else if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				parent = cur;
				cur = cur->_left;
			}
		}
		//找到空结点了，开始插入
		cur = new Node(kv);
		cur->_parent = parent;
		if (kv.first < parent->_kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		
		//以parent为起点，向上更新平衡因子，必要时进行调整
		//一个结点的平衡因子是否被影响，只需看它的子树高度是否发生变化
		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_bf--;
			}
			else
			{
				parent->_bf++;
			}
			
			if (parent->_bf == 0)//-1->0或者1->0,说明以parent为根结点的这颗树的高度没有变化,不用向上更新平衡因子了
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)//说明以parent为根结点的这颗子树高度+1，需要继续向上跟新平衡因子
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)//parent这个结点已经不平衡了，需要调整
			{
				if (cur->_bf == 1 && parent->_bf == 2)
				{
					//左单旋--parent和cur都是右边高
					rotateL(parent);
				}
				else if (cur->_bf == -1 && parent->_bf == -2)
				{
					//右单旋--parent和cur都是左边高
					rotateR(parent);
				}
				else if (cur->_bf == -1 && parent->_bf == 2)
				{
					//右左双旋--cur左边高，parent右边高
					rotateRL(parent);
				}
				else if (cur->_bf == 1 && parent->_bf == -2)
				{
					//左右双旋
					rotateLR(parent);
				}
				break;//调整后不用往上更新平衡因子了，因为以parent为根结点的这棵树插入前高度和调整后高度一样
			}
			else
			{
				cout << "平衡因子出错" << endl;
				assert(false);
			}
		}

		return true;
		
	}

	bool erase(const K& key)
	{
		//先找到它
		Node* cur = find(key);
		if (cur == nullptr)
		{
			return false;
		}
		if (key == 9798)
		{
			int i = 0;
		}
		//如果cur有两个孩子，则用右子树的最左结点替换它
		if (cur->_left && cur->_right)
		{
			Node* target = cur->_right;
			while (target->_left)
			{
				target = target->_left;
			}
			swap(cur->_kv, target->_kv);
			cur = target;
		}
		//删除cur
		Node* parent = cur->_parent;
		Node* lChild = cur->_left;
		Node* rChild = cur->_right;
		Node* child = nullptr;
		//1.cur右孩子为空
		if (rChild == nullptr)
		{
			child = lChild;
		}
		//2.cur左孩子为空
		else if (lChild == nullptr)
		{
			child = rChild;
		}
		else
		{
			cout << "替换结点有误" << endl;
			assert(false);
		}

		//parent和child构建关系
		//1.被删的cur是根结点
		if (parent == nullptr)
		{
			_root = child;
		}
		//2.被删的是一个普通结点，cur的父亲不为空
		else
		{
			if (cur == parent->_left)
			{
				parent->_left = child;
				parent->_bf++;
			}
			else
			{
				parent->_right = child;
				parent->_bf--;
			}
		}
		if (child)
		{
			child->_parent = parent;
		}
		
		delete cur;


		//开始更新平衡因子
		bool flag = false;
		while (parent)
		{
			//第一次进来不更新平衡因子
			if (flag)
			{
				if (child == parent->_left)
				{
					parent->_bf++;
				}
				else
				{
					parent->_bf--;
				}
			}
			flag = true;

			if (parent->_bf == 1 || parent->_bf == -1)//还是平衡的，树高度没有变，不需要向上处理
			{
				break;
			}
			else if (parent->_bf == 0)//高那颗子树删除了一个结点，树的高度降低，继续向上更新
			{
				child = parent;
				parent = parent->_parent;
 			}
			else if (parent->_bf == 2 || parent->_bf == -2)//不平衡了，需要调整
			{
				//child指向高的那颗子树
				if (parent->_bf > 0)
				{
					child = parent->_right;
				}
				else
				{
					child = parent->_left;
				}
				assert(child);

				Node* grandpa = parent->_parent;//提前记录parent的父节点，否则旋转后就找不到了
				//child和parent都是同一边高，或者child两边一样高，单旋即可
				if (child->_bf * parent->_bf >= 0)
				{
					int bf = child->_bf;
					if (parent->_bf == 2)
					{
						rotateL(parent);
						if (bf == 0)
						{
							parent->_bf = 1;
							child->_bf = -1;
						}
					}
					else
					{
						rotateR(parent);
						if (bf == 0)
						{
							parent->_bf = -1;
							child->_bf = 1;
						}
						
					}
					
					//判断是否还需要向上更新平衡因子
					//--当child原来的_bf = 0时parent这颗树删除前和调整后高度不变
					if (bf == 0)
					{
						break;
					}
					child = parent->_parent;
					parent = grandpa;
					
				}
				//parent和child的平衡因子符号不同--需要双旋
				else
				{
					if (parent->_bf == 2 && child->_bf == -1)
					{
						rotateRL(parent);
					}
					else if (parent->_bf == -2 && child->_bf == 1)
					{
						rotateLR(parent);
					}
					child = parent->_parent;
					parent = grandpa;
				}
			}
			else
			{
				cout << "平衡因子出错" << endl;
				assert(false);
			}
		}

		return true;
	}
	
	void inOrder()
	{
		_inOrder(_root);
	}
	
	bool isBalance()
	{
		return _isBalance(_root);
	}

	int height(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}
		return max(height(root->_left), height(root->_right)) + 1;
	}

protected:
	void rotateL(Node* parent)
	{
		Node* grandfather = parent->_parent;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		//grandfather和subR
		subR->_parent = grandfather;
		if (grandfather == nullptr)
		{
			_root = subR;
		}
		else
		{
			parent == grandfather->_left ? grandfather->_left = subR : grandfather->_right = subR;
		}

		//parent和subRL
		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}
		//subR和parent
		subR->_left = parent;
		parent->_parent = subR;

		subR->_bf = parent->_bf = 0;
	}

	void rotateR(Node* parent)
	{
		Node* grandpa = parent->_parent;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		
		//grandpa和subL
		subL->_parent = grandpa;
		if (grandpa == nullptr)
		{
			_root = subL;
		}
		else
		{
			parent == grandpa->_left ? grandpa->_left = subL : grandpa->_right = subL;
		}
		//parent和subLR
		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		//subL和parent
		parent->_parent = subL;
		subL->_right = parent;

		subL->_bf = parent->_bf = 0;
	}

	void rotateRL(Node* parent)//--本质是将subRL作为根结点，parent和subR成为它的左右护法，并将subRL的左右子树分给它们
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		rotateR(subR);
		rotateL(parent);
		//更新平衡因子
		if (bf == 0)//subRL自己就是新插入的结点
		{
			subR->_bf = subRL->_bf = parent->_bf = 0;
		}
		else if (bf == 1)//在subRL的右子树插入结点
		{
			subR->_bf = subRL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1)//在subRL的左子树插入结点
		{
			subRL->_bf = parent->_bf = 0;
			subR->_bf = 1;
		}
	}
	Node* _root = nullptr;

	void rotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
		rotateL(subL);
		rotateR(parent);

		//更新平衡因子
		if (bf == 0)//subLR自己就是新插入的结点
		{
			subLR->_bf = parent->_bf = subL->_bf = 0;
		}
		else if (bf == -1)//在subLR左子树插入结点
		{
			subLR->_bf = subL->_bf = 0;
			parent->_bf = 1;
		}
		else if (bf == 1)//在subLR右子树插入结点
		{
			subLR->_bf = parent->_bf = 0;
			subL->_bf = -1;
		}
	}

	void _inOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_inOrder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << " ";
		_inOrder(root->_right);
	}

	bool _isBalance(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}
		int leftHeight = height(root->_left);
		int rightHeight = height(root->_right);
		if (rightHeight - leftHeight != root->_bf)
		{
			cout << root->_kv.first << "平衡因子出错:实际" << rightHeight - leftHeight << "记录" << root->_bf << endl;
			return false;
		}

		return abs(leftHeight - rightHeight) <= 1
			&& _isBalance(root->_left)
			&& _isBalance(root->_right);
	} 
};

一些说明：

四个旋转函数包含了平衡因子的调节，这是以插入时的四种情况为准(因为我是先实现的插入)，删除有几种情况平衡因子还需要自己调节。建议大家实现旋转函数时不包含平衡因子调节。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1209021.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

修改Openwrt软路由的web端口

修改Openwrt软路由的web端口

如何修改openwrt路由器的web访问端口号&#xff1f; 在OpenWrt路由器上&#xff0c;如何修改Web访问端口号&#xff0c;通常涉及到修改HTTP服务器的配置文件。默认情况下&#xff0c;OpenWrt使用的HTTP服务器是uHTTPd。 以下是修改Web访问端口号的步骤&#xff1a; 一、通过…
阅读更多...
【LeetCode刷题-双指针】--80.删除有序数组中的重复项II

【LeetCode刷题-双指针】--80.删除有序数组中的重复项II

80.删除有序数组中的重复项II 方法&#xff1a;双指针 因为给定数组是有序的&#xff0c;所以相同元素必然连续&#xff0c;使用双指针解决&#xff0c;遍历数组检查每一个元素是否应该被保留&#xff0c;如果应该保留&#xff0c;就将其移动到指定位置。我们定义两个指针slow…
阅读更多...
【LeetCode刷题-滑动窗口】-- 643.子数组最大平均数I

【LeetCode刷题-滑动窗口】-- 643.子数组最大平均数I

643.子数组最大平均数I 方法&#xff1a;滑动窗口 class Solution {public double findMaxAverage(int[] nums, int k) {int n nums.length;int winSum 0;//先求出第一个窗口的和for(int i 0;i<k;i){winSum nums[i];}//通过遍历求出除了第一窗口的和int res winSum;fo…
阅读更多...
ChatGPT只算L1阶段，谷歌提出AGI完整路线图

ChatGPT只算L1阶段，谷歌提出AGI完整路线图

按照谷歌这个标准来看&#xff0c;大多数已有AI产品其实都分别进入了不同的AGI阶段&#xff0c;但只仅限于在技能水平上——要谈及通用性&#xff0c;目前只有ChatGPT等模型完全合格。 AGI应该如何发展、最终呈什么样子&#xff1f; 现在&#xff0c;业内第一个标准率先发布&a…
阅读更多...
【Linux网络】ssh服务与配置，实现安全的密钥对免密登录

【Linux网络】ssh服务与配置，实现安全的密钥对免密登录

目录 一、SSH基础 1、什么是ssh服务器 2、对比一下ssh协议与telnet协议 3、常见的底层为ssh协议的软件&#xff1a; 4、拓展 二、SSH软件学习 1、ssh服务软件学习 2、sshd公钥传输的原理&#xff1a; 3、ssh命令学习&#xff1a; 4、学习解读sshd服务配置文件&#x…
阅读更多...
spring cloud-注册中心（Eureka）

spring cloud-注册中心（Eureka）

一、服务注册中心组件(*) 定义&#xff1a;服务注册中心就是在整个微服务架构单独抽取一个服务&#xff0c;该服务不做项目中任何业务功能&#xff0c;仅用来在微服务中记录微服务、对微服务进行健康状态检查&#xff0c;及服务元数据信息存储常用的注册中心&#xff1a;eurek…
阅读更多...
【JAVA学习笔记】70 - 反射

【JAVA学习笔记】70 - 反射

项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter23/src 反射 一、反射的引出 package com.yinhai.reflection.question;import com.yinhai.Cat;import java.io.FileInputStream; import java.io.FileNotFoundException; import java.io.IO…
阅读更多...
双点重发布+路由策略实验

双点重发布+路由策略实验

一、双点重发布实验 1、实验拓扑图 2、各路由器IP地址、环回地址配置 R1 R2 R3 R4 3、启动RIP和OSPF 4、双向重发布 5、查看路由信息 6、更改网络类型 6、抓取流量 二、路由策略实验 1、实验拓扑图 2、各路由器IP地址的配置 3、启动RIP和OSPF 3、重发布 4、抓取流量 5、创建…
阅读更多...
【算法练习Day48】回文子串最长回文子序列

【算法练习Day48】回文子串最长回文子序列

​&#x1f4dd;个人主页&#xff1a;Sherry的成长之路 &#x1f3e0;学习社区&#xff1a;Sherry的成长之路&#xff08;个人社区&#xff09; &#x1f4d6;专栏链接&#xff1a;练题 &#x1f3af;长路漫漫浩浩&#xff0c;万事皆有期待 文章目录 回文子串最长回文子序列总结…
阅读更多...
C#几种截取字符串的方法

C#几种截取字符串的方法

在C#编程中&#xff0c;经常需要对字符串进行截取操作&#xff0c;即从一个长字符串中获取所需的部分信息。本文将介绍几种常用的C#字符串截取方法&#xff0c;并提供相应的示例代码。 目录 1. 使用Substring方法2. 使用Split方法3. 使用Substring和IndexOf方法4. 使用Regex类…
阅读更多...
Zabbix 5.0部署（centos7+server+MySQL+Apache）

Zabbix 5.0部署（centos7+server+MySQL+Apache）

环境 系统IPZABBIX版本主机名centos7192.168.231.2195.0zabbix-server 安装zabbix 我选择版本是zabbix-5.0 zabbix的官网是Zabbix :: The Enterprise-Class Open Source Network Monitoring Solution 安装Zabbix软件源 rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/…
阅读更多...
关于Flume-Kafka-Flume的模式进行数据采集操作

关于Flume-Kafka-Flume的模式进行数据采集操作

测试是否连接成功&#xff1a; 在主节点flume目录下输入命令: bin/flume-ng agent -n a1 -c conf/ -f job/file_to_kafka.conf -Dflume.root.loggerinfo,console # 这个file_to_kafka.conf文件就是我们的配置文件 然后在另一台节点输入命令进行消费数据&#xff1a; kafka-cons…
阅读更多...
Java Stream 的使用

Java Stream 的使用

Java Stream 的使用 开始中间操作forEach 遍历map 映射flatMap 平铺filter 过滤limit 限制sorted 排序distinct 去重 结束操作collect 收集toList、toSet 和 toMapCollectors.groupingByCollectors.collectingAndThen metch 匹配find 查询findFirst 与 findAny 的使用Optional …
阅读更多...
下载免费商用字体，就上这6个网站。

下载免费商用字体，就上这6个网站。

我不允许还有人不知道&#xff0c;这些可以免费下载商用字体的网站&#xff0c;必须收藏好了&#xff0c;有了这6个网站&#xff0c;再也不用担心字体侵权了。 1、字体搬运工 https://font.sucai999.com/ 一个免费可商用字体搬运工&#xff0c;实时跟新市面上免费商用的字体。…
阅读更多...
No204.精选前端面试题，享受每天的挑战和学习

No204.精选前端面试题，享受每天的挑战和学习

🤍 前端开发工程师（主业）、技术博主（副业）、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…
阅读更多...
java程序中为什么经常使用tomcat

java程序中为什么经常使用tomcat

该疑问的产生场景&#xff1a; 原来接触的ssm项目需要在项目配置中设置tomcat&#xff0c;至于为什么要设置tomcat不清楚&#xff0c;只了解需要配置tomcat后项目才能启动。接触的springboot在项目配置中不需要配置tomcat&#xff0c;原因是springboot框架内置了tomcat&#xf…
阅读更多...
1、 图像和像素

1、 图像和像素

像素我们不陌生，图像我们更不陌生。 学习计算机视觉，我觉得第一步就是要了解我们要处理的对象，就像上一篇说到的，计算机视觉任务中，图像（像素）是原材料，算法是菜谱。 了解了图像的特征，才可以更好的完成更多图像处理任务，比如对一张图片进行分类，或者对一张图片画…
阅读更多...
CNN进展：AlexNet、VGGNet、ResNet 和 Inception

CNN进展：AlexNet、VGGNet、ResNet 和 Inception

一、说明 对于初学者来说&#xff0c;神经网络进展的历程有无概念&#xff1f;该文综合叙述了深度神经网络的革命性突破&#xff0c;从AlexNet开始&#xff0c;然后深度VGG的改进&#xff0c;然后是残差网络ResNet和 Inception&#xff0c;如果能讲出各种特色改进点的和改进理由…
阅读更多...
【Python】【应用】Python应用之一行命令搭建http、ftp服务器

【Python】【应用】Python应用之一行命令搭建http、ftp服务器

&#x1f41a;作者简介&#xff1a;花神庙码农&#xff08;专注于Linux、WLAN、TCP/IP、Python等技术方向&#xff09;&#x1f433;博客主页&#xff1a;花神庙码农 &#xff0c;地址&#xff1a;https://blog.csdn.net/qxhgd&#x1f310;系列专栏&#xff1a;Python应用&…
阅读更多...
MQ四大消费问题一锅端：消息不丢失 + 消息积压 + 重复消费 + 消费顺序性

MQ四大消费问题一锅端：消息不丢失 + 消息积压 + 重复消费 + 消费顺序性

RabbitMQ-如何保证消息不丢失 生产者把消息发送到 RabbitMQ Server 的过程中丢失 从生产者发送消息的角度来说&#xff0c;RabbitMQ 提供了一个 Confirm&#xff08;消息确认&#xff09;机制&#xff0c;生产者发送消息到 Server 端以后&#xff0c;如果消息处理成功&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023