物理问题中常见的分析问题----什么样的函数性质较好

news2024/11/25 21:40:27
  • 物理问题中常见的积分符号位置交换问题

重极限与累次极限

  • 高数下的定义
    • 累次极限：求极限时需要遵循一定的顺序
    • 重极限：任意方向趋于的极限

  • 两者之间的关系：
    • 两者没啥关系
  • 存在累次极限存在而不相等的函数
  • ......

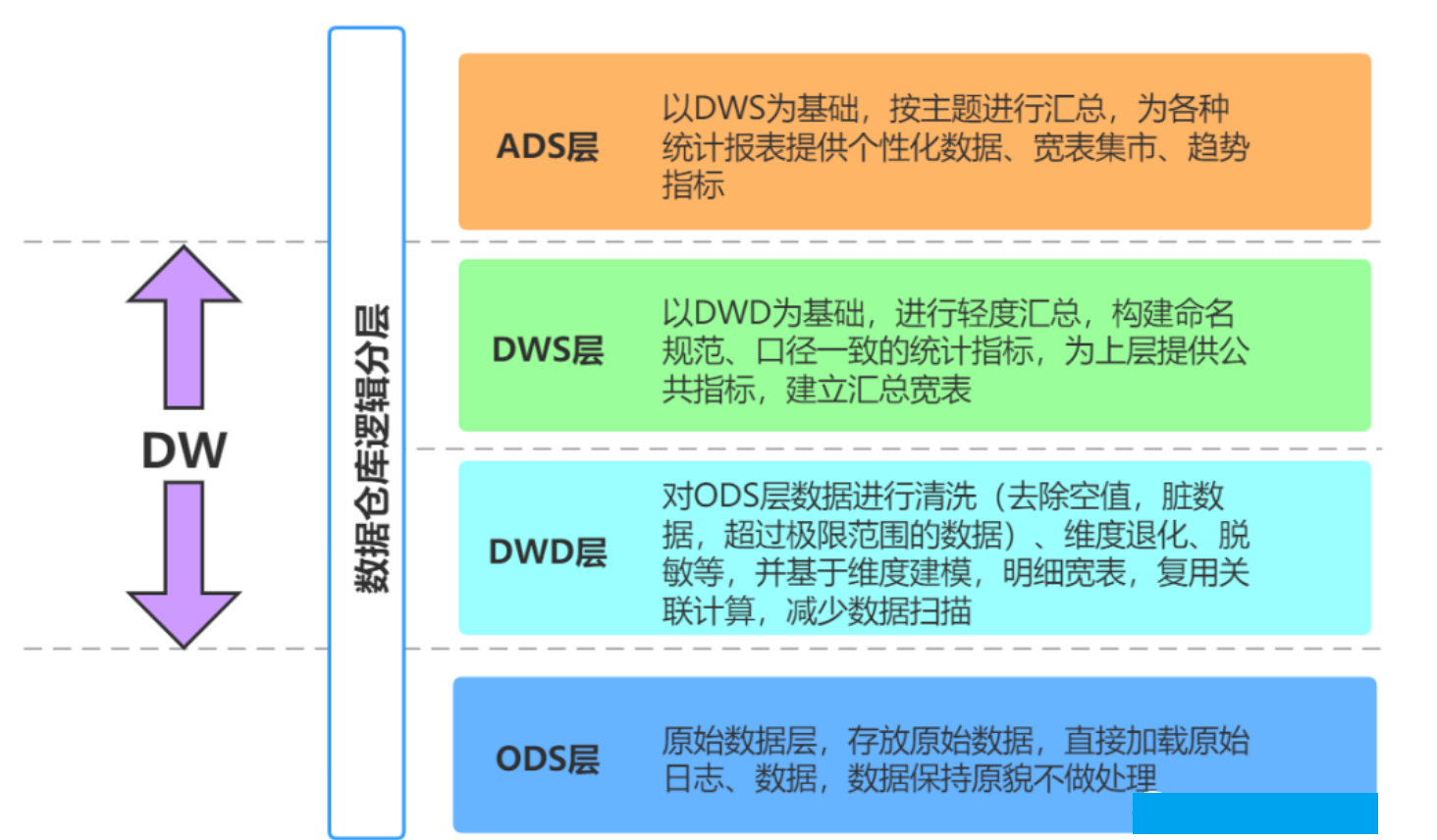
求和符号与积分符号互换--逐项积分问题

  • 一致收敛性的定义级别判定方法----柯西判别法
  • 函数项级数\sum u_n一致收敛的充分必要条件是对于任意给定的\varepsilon>0，存在正整数N=N(\varepsilon)使得|u_{n+1}+u_{n+2}+...+u_m(x)|<\varepsilon对一切m>n>N成立

  • 一致收敛性的判别方法之一----外尔斯特拉斯方法
  • 设\sum u_n(x)是一个函数项级数，若存在一个收敛的正项级数\sum v_n且存在N当n>N时|u_n|<v_n，那么函数项级数\sum u_n(x)一致收敛

  • 一致收敛性的判别方法之一----比较判别法
  • 设\sum u_n(x)是一个函数项级数，设q_n(x)=\frac{u_{n+1}(x)}{u_n(x)}，存在正整数N以及实数q,M使得q_n(x)\leq q < 1,u_n(x)\leq M对任意n>N,x\in D成立，则函数项级数在D上一致收敛

  • 一致收敛性的判别方法之一----根式判别法
  • 设\sum u_n(x)是一个函数项级数，若存在一个正整数N使得^n\sqrt{|u_n(x)|}\leq q \leq 1对于所有n>N,x\in D成立，那么函数项级数在D上一致收敛

  • 一致收敛性的判别方法
    • 狄利克雷方法
    • 阿贝尔方法

  • 函数项级数\sum_{n=1}^\infty u_n(x)在[a,b]上一致收敛于f(x)且所有的u_n(x)在[a,b]上可积，那么\int_a^bf(x)dx=\int_a^b(\sum_{n=1}^\infty u(x))dx=\sum_{n=1}^\infty \int_a^b u_n(x)dx

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1208378.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

python 随机密码生成器

python 随机密码生成器

最近在研究PySimpleGUI库&#xff0c;把之前写的一个随机密码生成器改成GUI版本发出来&#xff0c;有兴趣的兄弟们可以拿走。 因为能力有限&#xff0c;目前只能写生成一个随机密码的Gui版本&#xff0c;等我学了更多的内容再慢慢完善。 核心代码很简单&#xff0c;界面也很粗陋…
阅读更多...
C语言从入门到精通之【字符串】

C语言从入门到精通之【字符串】

C语言没有专门用于储存字符串的变量类型&#xff0c;字符串都被储存在char类型的数组中。数组由连续的存储单元组成&#xff0c;字符串中的字符被储存在相邻的存储单元中&#xff0c;每个单元储存一个字符&#xff0c;每个字符占1个字节。 数组末尾位置的字符\0。这是空字符&am…
阅读更多...
[Kettle] 记录处理

[Kettle] 记录处理

1.排序记录 排序是对数据中的无序记录&#xff0c;按照自然或客观规律&#xff0c;根据关键字段大小递增或递减的次序&#xff0c;对记录重新排列的过程 数据源 2019年11月月考数学成绩(Kettle数据集3).xlshttps://download.csdn.net/download/Hudas/88521681 2019年11月月考…
阅读更多...
【10套模拟】【4】

【10套模拟】【4】

关键字&#xff1a; 二分查找比较次数、*广义表头尾链表存储、森林转二叉树、链地址法哈希表、交换所有子树、创建二叉排序树
阅读更多...
【10套模拟】【3】

【10套模拟】【3】

关键字&#xff1a; 物理存储、完全二叉树、出栈入栈时间复杂度、线索二叉树
阅读更多...
【云上探索实验室】快速入门AI 编程助手 Amazon CodeWhisperer ——码上学堂领学员招募

【云上探索实验室】快速入门AI 编程助手 Amazon CodeWhisperer ——码上学堂领学员招募

目录 一、Amazon CodeWhisperer1.1、大语言模型与AI编程1.2、CodeWhisperer初体验 二、云上探索实验室-码上学堂2.1、码上学堂2.2、学课通道入口 三、领学员招募3.1、报名方式3.2、领学奖励 一、Amazon CodeWhisperer 1.1、大语言模型与AI编程 大语言模型&#xff08;Large L…
阅读更多...
如何理解 Linux 当中 “一切皆文件“

如何理解 Linux 当中 “一切皆文件“

我们在 操作系统 当中的所有操作&#xff0c;包括对文件的所有操作&#xff0c;最终其实都是 通过 进程来实现的。 我们想象我们实现的各种C/C 程序&#xff0c;或者是各种语言实现的程序&#xff0c;本质上都是要 编译形成 可执行文件&#xff0c;然后操作系统把这个可执行文…
阅读更多...
设备数据如何为预测性维护提供支持

设备数据如何为预测性维护提供支持

预测性维护是现代制造业中一种高效而受欢迎的维护策略&#xff0c;它能够帮助企业提前发现设备故障的早期迹象&#xff0c;并采取相应措施&#xff0c;从而避免生产线的停机和生产效率的下降。实施预测性维护的关键在于充分利用设备数据&#xff0c;通过数据的收集、处理和分析…
阅读更多...
浏览器Cookie是什么？如何在MaskFog指纹浏览器中导入Cookie？

浏览器Cookie是什么？如何在MaskFog指纹浏览器中导入Cookie？

在使用互联网时我们常常听到cookie这个词&#xff0c;那到底什么是cookie呢&#xff1f; Cookie是某些网站为了辨别用户身份而储存在用户本地终端上的数据&#xff08;通常经过加密&#xff09;&#xff0c;由用户客户端计算机暂时或永久保存的信息客户端向服务器发起请求&…
阅读更多...
C语言从入门到精通之【char类型】

C语言从入门到精通之【char类型】

char类型用于储存字符&#xff08;如&#xff0c;字母或标点符号&#xff09;&#xff0c;但是从技术层面看&#xff0c;char是整数类型。因为char类型实际上储存的是整数而不是字符。计算机使用数字编码来处理字符&#xff0c;即用特定的整数表示特定的字符。 char类型占1个字…
阅读更多...
循环服务器

循环服务器

一、服务器模型 在网络程序里面,通常都是一个服务器处理多 个客户机。为了处理多个客户机的请求, 服务器端的程序有不同的处理方式。 1、循环服务器模型 socket()&#xff1b; bind(); liste(); while(1) { accept(); while(1) { recv ret0; break; } close(acceptfd); } close…
阅读更多...
《使用EasyExcel在Excel中增加序号列的方法》

《使用EasyExcel在Excel中增加序号列的方法》

《使用EasyExcel在Excel中增加序号列的方法》 1、简介2、正文3、核心代码4、使用方法5、效果 1、简介 在处理Excel文件时&#xff0c;有时候需要为表格增加序号列。本文介绍了如何使用Java代码实现在Excel中增加序号列的功能&#xff0c;并提供了一个示例代码。 2、正文 在处理…
阅读更多...
2023.11.14-hive的类SQL表操作之,4个by区别

2023.11.14-hive的类SQL表操作之,4个by区别

目录 1.表操作之4个by,分别是 2.Order by:全局排序 3.Cluster by 4.Distribute by :分区 5. Sort by :每个Reduce内部排序 6.操作练习 步骤一.创建表 步骤二.加载数据 步骤三.验证数据 1.表操作之4个by,分别是 order by 排序字段名 cluster by 分桶并排序字段名 dis…
阅读更多...
异常与中断（一）

异常与中断（一）

使用生活实例引入中断 假设有个大房间里面有小房间&#xff0c;婴儿正在睡觉&#xff0c;他的妈妈在外面看书。 问&#xff1a;这个母亲怎么才能知道这个小孩醒&#xff1f; 过一会打开一次房门&#xff0c;看婴儿是否睡醒&#xff0c;然后接着看书一直等到婴儿发出声音以后再…
阅读更多...
SQL之回炉重造

SQL之回炉重造

重新学sql&#xff0c;整个知识框架出来&#xff0c;之前学的太烂了 SQL是什么&#xff1a; SQL 是一种操作数据库的语言&#xff0c;包括创建数据库、删除数据库、查询记录、修改记录、添加字段等。SQL 虽然是一种被 ANSI 标准化的语言&#xff0c;但是它有很多不同的实现版…
阅读更多...
医疗行业创新：低代码工具推动业务自动化和智能化

医疗行业创新：低代码工具推动业务自动化和智能化

随着科技的不断发展&#xff0c;数字化已经成为各个领域的必然趋势。同样&#xff0c;在医疗领域&#xff0c;数字化转型也已经成为必要性。 早在新冠疫情之前很多国家和地区就已经开始尝试医疗数字化的转型。有很多人认为&#xff0c;医疗数字化在未来不是锦上添花&#xff0…
阅读更多...
黑客泄露 3500 万条 LinkedIn 用户记录

黑客泄露 3500 万条 LinkedIn 用户记录

被抓取的 LinkedIn 数据库分为两部分泄露&#xff1a;一部分包含 500 万条用户记录&#xff0c;第二部分包含 3500 万条记录。 LinkedIn 数据库保存了超过 3500 万用户的个人信息&#xff0c;被化名 USDoD 的黑客泄露。 该数据库在臭名昭著的网络犯罪和黑客平台 Breach Forum…
阅读更多...
langchain实战-hello world

langchain实战-hello world

一、LangChain简介 github地址&#xff1a; GitHub - langchain-ai/langchain: ⚡ Building applications with LLMs through composability ⚡ LangChain是一个用于开发由语言模型支持的应用程序的框架。它使应用程序能够&#xff1a; 具有上下文感知能力&#xff1a;将语言模…
阅读更多...
【左程云算法全讲7】二叉树基础算法及递归套路

【左程云算法全讲7】二叉树基础算法及递归套路

系列综述&#xff1a; &#x1f49e;目的&#xff1a;本系列是个人整理为了秋招面试的&#xff0c;整理期间苛求每个知识点&#xff0c;平衡理解简易度与深入程度。 &#x1f970;来源&#xff1a;材料主要源于左程云算法课程进行的&#xff0c;每个知识点的修正和深入主要参考…
阅读更多...
【数据仓库】数仓分层方法详解与层次调用规范

【数据仓库】数仓分层方法详解与层次调用规范

文章目录 一. 数仓分层的意义1. 清晰数据结构。2. 减少重复开发3. 方便数据血缘追踪4. 把复杂问题简单化5. 屏蔽原始数据的异常6. 数据仓库的可维护性 二. 如何进行数仓分层&#xff1f;1. ODS层2. DW层2.1. DW层分类2.2. DWD层2.3. DWS 3. ADS层 4、层次调用规范 一. 数仓分层…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023