前言

小编研究生的研究方向是视觉SLAM，目前在自学，本篇文章为初学高翔老师课的第四次作业。

---

1.图像去畸变

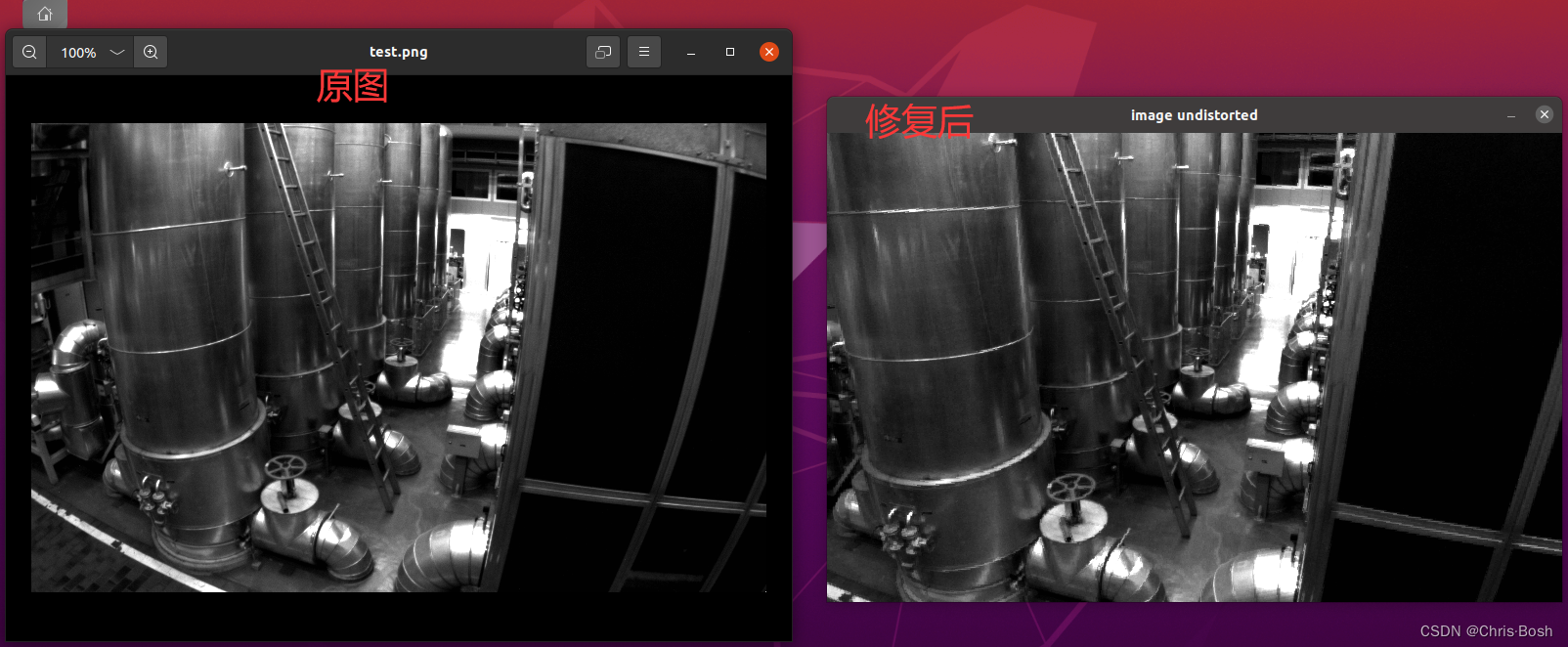
现实⽣活中的图像总存在畸变。原则上来说，针孔透视相机应该将三维世界中的直线投影成直线，但是当我们使⽤⼴⾓和鱼眼镜头时，由于畸变的原因，直线在图像⾥看起来是扭曲的。本次作业，你将尝试如何对⼀张图像去畸变，得到畸变前的图像。

对于畸变，用两张鲜明的照片来展示：


undistort_image.cpp：

//
// Created by ljh on 2023/11/5.
//

#include <opencv2/opencv.hpp>
#include <string>

using namespace std;

string image_file = "/home/lih/video4_homework/homework1/test.png"; // 请确保路径正确

int main(int argc, char **argv) {

    // 本程序需要你自己实现去畸变部分的代码。尽管我们可以调用OpenCV的去畸变，但自己实现一遍有助于理解。
    // 畸变参数
    double k1 = -0.28340811, k2 = 0.07395907, p1 = 0.00019359, p2 = 1.76187114e-05;
    // 内参
    double fx = 458.654, fy = 457.296, cx = 367.215, cy = 248.375;

    cv::Mat image = cv::imread(image_file,0);   // 图像是灰度图，CV_8UC1
    int rows = image.rows, cols = image.cols;
    cv::Mat image_undistort = cv::Mat(rows, cols, CV_8UC1);   // 去畸变以后的图

    // 计算去畸变后图像的内容
    for (int v = 0; v < rows; v++)
        for (int u = 0; u < cols; u++) {

            double u_distorted = 0, v_distorted = 0;
            // TODO 按照公式，计算点(u,v)对应到畸变图像中的坐标(u_distorted, v_distorted) (~6 lines)
            // start your code here
            // 按照公式，计算点(u,v)对应到畸变图像中的坐标(u_distorted, v_distorted)
double x = (u-cx)/fx, y = (v-cy)/fy; 

// 计算图像点坐标到光心的距离；
double r = sqrt(x*x+y*y);

// 计算投影点畸变后的点
double x_distorted = x*(1+k1*r+k2*r*r)+2*p1*x*y+p2*(r+2*x*x); 
double y_distorted = y*(1+k1*r+k2*r*r)+2*p2*x*y+p1*(r+2*y*y); 

// 把畸变后的点投影回去
u_distorted = x_distorted*fx+cx;
v_distorted = y_distorted*fy+cy;
            // end your code here

            // 赋值 (最近邻插值)
            if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < cols && v_distorted < rows) {
                image_undistort.at<uchar>(v, u) = image.at<uchar>((int) v_distorted, (int) u_distorted);
            } else {
                image_undistort.at<uchar>(v, u) = 0;
            }
        }

    // 画图去畸变后图像
    cv::imshow("image undistorted", image_undistort);
    cv::waitKey();

    return 0;
}

string image_file = “/home/lih/video4_homework/homework1/test.png”; // 填写你自己的图片路径

CMakeLists.txt：

cmake_minimum_required(VERSION 2.8)

PROJECT(undistort_image)

IF(NOT CMAKE_BUILD_TYPE) #（可选）如果没有指定cmake编译模式，就选择Relealse模式，必须写成三行
    SET(CMAKE_BUILD_TYPE Release)
ENDIF()

MESSAGE("Build type: " ${CMAKE_BUILD_TYPE}) #终端打印cmake编译模式的信息

set(CMAKE_C_FLAGS "${CMAKE_C_FLAGS}  -Wall  -O3 -march=native ") #添加c标准支持库
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -Wall   -O3 -march=native") #添加c++标准支持库

# Check C++11 or C++0x support #检查c++11或c++0x标准支持库
include(CheckCXXCompilerFlag)
CHECK_CXX_COMPILER_FLAG("-std=c++11" COMPILER_SUPPORTS_CXX11)
CHECK_CXX_COMPILER_FLAG("-std=c++0x" COMPILER_SUPPORTS_CXX0X)
if(COMPILER_SUPPORTS_CXX11)
    set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11")
    add_definitions(-DCOMPILEDWITHC11)
    message(STATUS "Using flag -std=c++11.")
elseif(COMPILER_SUPPORTS_CXX0X)
    set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++0x")
    add_definitions(-DCOMPILEDWITHC0X)
    message(STATUS "Using flag -std=c++0x.")
else()
    message(FATAL_ERROR "The compiler ${CMAKE_CXX_COMPILER} has no C++11 support. Please use a different C++ compiler.")
endif()

find_package(OpenCV 3.0 QUIET) #find_package(<Name>)命令首先会在模块路径中寻找 Find<name>.cmake
if(NOT OpenCV_FOUND)
    find_package(OpenCV 2.4.3 QUIET)
    if(NOT OpenCV_FOUND)
        message(FATAL_ERROR "OpenCV > 2.4.3 not found.")
    endif()
endif()

include_directories(${OpenCV_INCLUDE_DIRS})

add_executable(image undistort_image.cpp)

#链接OpenCV库
target_link_libraries(image ${OpenCV_LIBS})

然后
mkdir build
cd build
cmake …
make
./image

2.双目视差的使用

双⽬相机的⼀⼤好处是可以通过左右⽬的视差来恢复深度。课程中我们介绍了由视差计算深度的过程。本题，你需要根据视差计算深度，进⽽⽣成点云数据。本题的数据来⾃Kitti 数据集 [2]。 Kitti中的相机部分使⽤了⼀个双⽬模型。双⽬采集到左图和右图，然后我们可以通过左右视图恢复出深度。经典双⽬恢复深度的算法有 BM(Block Matching), SGBM(Semi-Global Matching)[3, 4]等，但本题不探讨⽴体视觉内容（那是⼀个⼤问题）。我们假设双⽬计算的视差已经给定，请你根据双⽬模型，画出图像对应的点云，并显⽰到 Pangolin 中。题给定的左右图见 code/left.png 和 code/right.png，视差图亦给定，见code/right.png。双⽬的参数如下：
f_x= 718.856; f_y = 718.856; c_x =607.1928; c_y = 185.2157
且双⽬左右间距（即基线）为：
d = 0.573 m
请根据以上参数，计算相机数据对应的点云，并显⽰到 Pangolin 中。程序请code/disparity.cpp ⽂件。

disparity.cpp：

           // start your code here
            // 根据双目模型计算 point 的位置
            double x = (u - cx) / fx;
            double y = (v - cy) / fy;
            double depth = fx * b / (disparity.at<float>(v, u));
            point[0] = x * depth;
            point[1] = y * depth;
            point[2] = depth;
             // end your code here

double x和double y的计算方式和上一题一样,depth就算如下：

计算出depth后，那么point模仿课上五对图片那个实践仿写即可。只不过实践中的d(视差)没有给出，而此题中视差d已给，所以公式写出来略有不同。
CMakeLists.txt:

cmake_minimum_required( VERSION 2.8 )
project(stereoVision)
set( CMAKE_CXX_FLAGS "-std=c++11 -O3")
 
include_directories("/usr/include/eigen3")
find_package(Pangolin REQUIRED)
include_directories( ${Pangolin_INCLUDE_DIRS} )
 
find_package(OpenCV 3.0 QUIET) #find_package(<Name>)命令首先会在模块路径中寻找 Find<name>.cmake
if(NOT OpenCV_FOUND)
    find_package(OpenCV 2.4.3 QUIET)
    if(NOT OpenCV_FOUND)
        message(FATAL_ERROR "OpenCV > 2.4.3 not found.")
    endif()
endif()

include_directories(${OpenCV_INCLUDE_DIRS})
 
add_executable(disparity disparity.cpp)
target_link_libraries(disparity ${OpenCV_LIBRARIES})
target_link_libraries(disparity ${Pangolin_LIBRARIES})

然后就是编译五部曲：
mkdir build
cd build
cmake …
make
./disparity

如果你出现了这张图片，那就是你的disparity.cpp中的图片位置没有写对，找不到图片所导致的！！

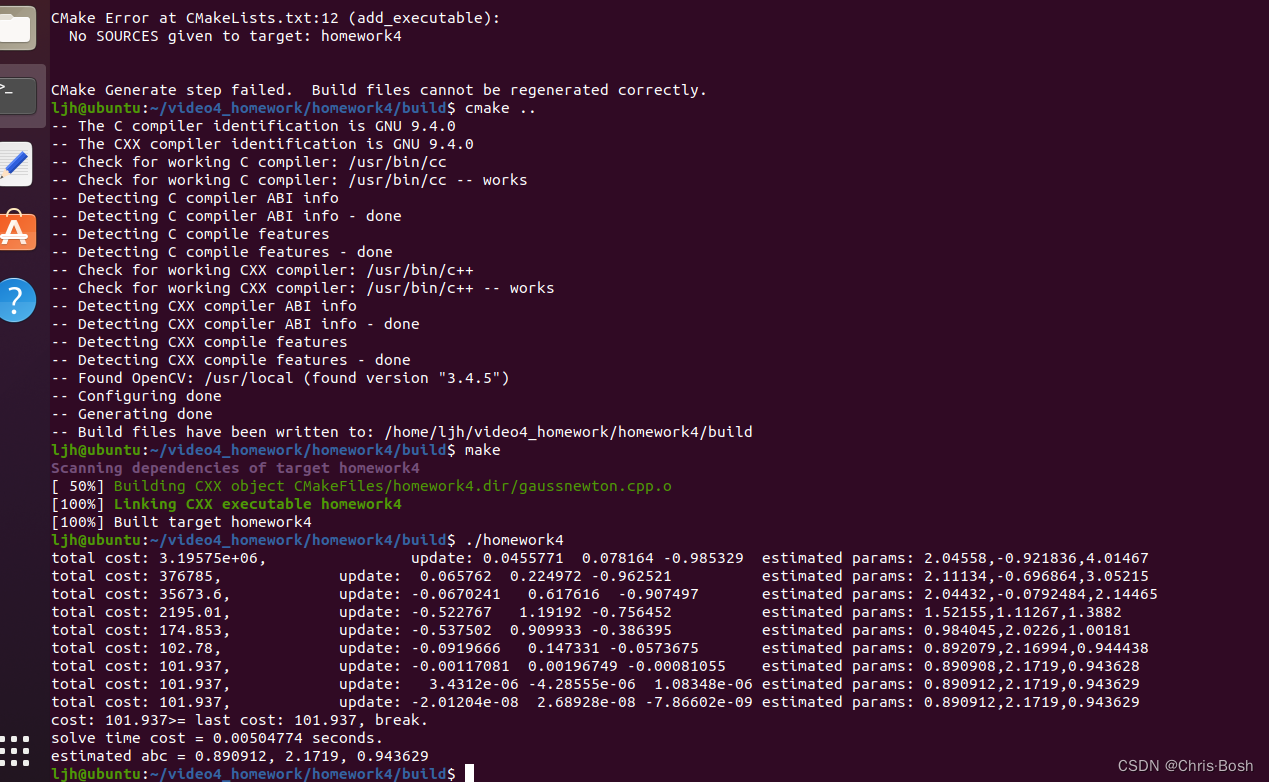
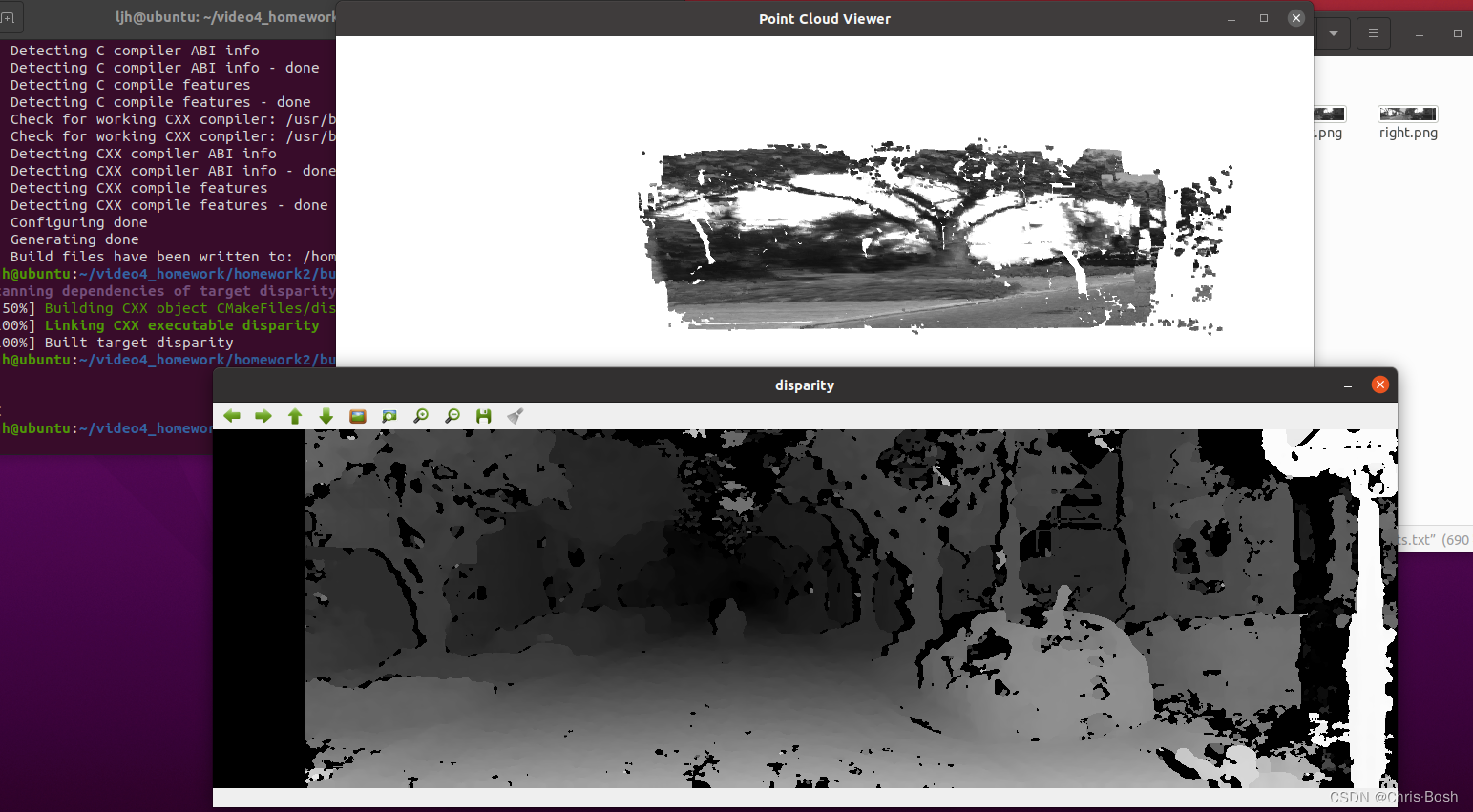
运行成功如下：

3.矩阵微分

①第一问：如果大家有不理解的地方可以看看这个印度三哥的视屏，我认为讲的还是非常清晰的，至少我搜了很多国内的都没有这个讲得好，虽然语言不通，但是一点都不影响学习。高博的清华PPT还是不适合我这种人看。
链接:
矩阵求导讲解

②第二问：如果大家有不理解的地方可以看看这个印度三哥的视屏，我认为讲的还是非常清晰的，至少我搜了很多国内的都没有这个讲得好，虽然语言不通，但是一点都不影响学习。高博的清华PPT还是不适合我这种人看。
链接:
矩阵求导讲解

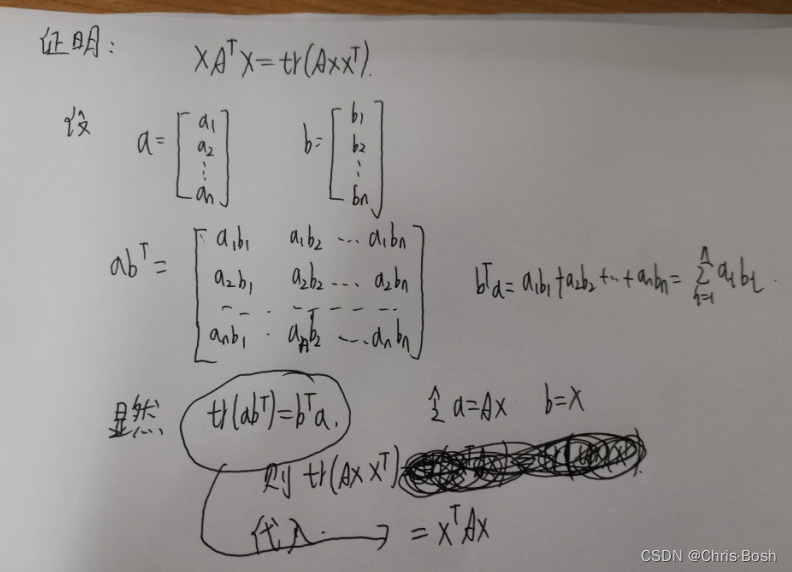
③第三问：

4.高斯牛顿法的曲线拟合实验

当然我觉得大家很有必要了解一下这一块的由来，我的上一篇博客讲述了海斯矩阵，凸函数等基本概念，大家看这个之前我认为很必要学习一下： 链接:
SLAM第四讲实践中的最优化知识

在做这道题之前我们非常有必要了解一下什么是牛顿法法，因为高斯牛顿法是牛顿法的改进，我以一道最优化的简单立体让你明白什么是牛顿法：


下来我们再看高斯牛顿法，我搜查了很多资料，很难找到一道高斯牛顿法的数学题来让大家理解，所以我只能找到一个更为详细点的高斯牛顿法的计算步骤让大家理解：

到这里，我们开始做题：
gaussnewton.cpp：

#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>
 
using namespace std;
using namespace Eigen;
 
int main(int argc, char **argv) {
  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器
 
  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }
 
  // 开始Gauss-Newton迭代
  int iterations = 100;    // 迭代次数
  double cost = 0, lastCost = 0;  // 本次迭代的cost和上一次迭代的cost
 
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  for (int iter = 0; iter < iterations; iter++) {
 
    Matrix3d H = Matrix3d::Zero();             // Hessian = J^T W^{-1} J in Gauss-Newton
    Vector3d b = Vector3d::Zero();             // bias
    cost = 0;
 
    for (int i = 0; i < N; i++) {
      double xi = x_data[i], yi = y_data[i];  // 第i个数据点
      double error = yi - exp(ae * xi * xi + be * xi + ce);//计算雅可比矩阵J（Xk）和误差f(Xk)
      Vector3d J; // 雅可比矩阵
      J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce);  // de/da
      J[1] = -xi * exp(ae * xi * xi + be * xi + ce);  // de/db
      J[2] = -exp(ae * xi * xi + be * xi + ce);  // de/dc
 
      H += inv_sigma * inv_sigma * J * J.transpose();
      b += -inv_sigma * inv_sigma * error * J;
 
      cost += error * error;
    }
 
    // 求解线性方程 Hx=b
    Vector3d dx = H.ldlt().solve(b);
    if (isnan(dx[0])) {
      cout << "result is nan!" << endl;
      break;
    }
 
    if (iter > 0 && cost >= lastCost) {
      cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
      break;
    }
 
    ae += dx[0];
    be += dx[1];
    ce += dx[2];
 
    lastCost = cost;
 
    cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
         "\t\testimated params: " << ae << "," << be << "," << ce << endl;
  }
 
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
 
  cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
  return 0;
}

CMakeLists.txt：

cmake_minimum_required(VERSION 2.8)
project(homework4)
set(CMAKE_BUILD_TYPE Release)
set(CMAKE_CXX_FLAGS "-std=c++14 -O3")
list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)
# OpenCV
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
# Eigen
include_directories("/usr/include/eigen3")

add_executable(homework4 gaussnewton.cpp)
target_link_libraries(homework4 ${OpenCV_LIBS})

然后老五套
mkdir build
cd build
cmake …
make
./homework4