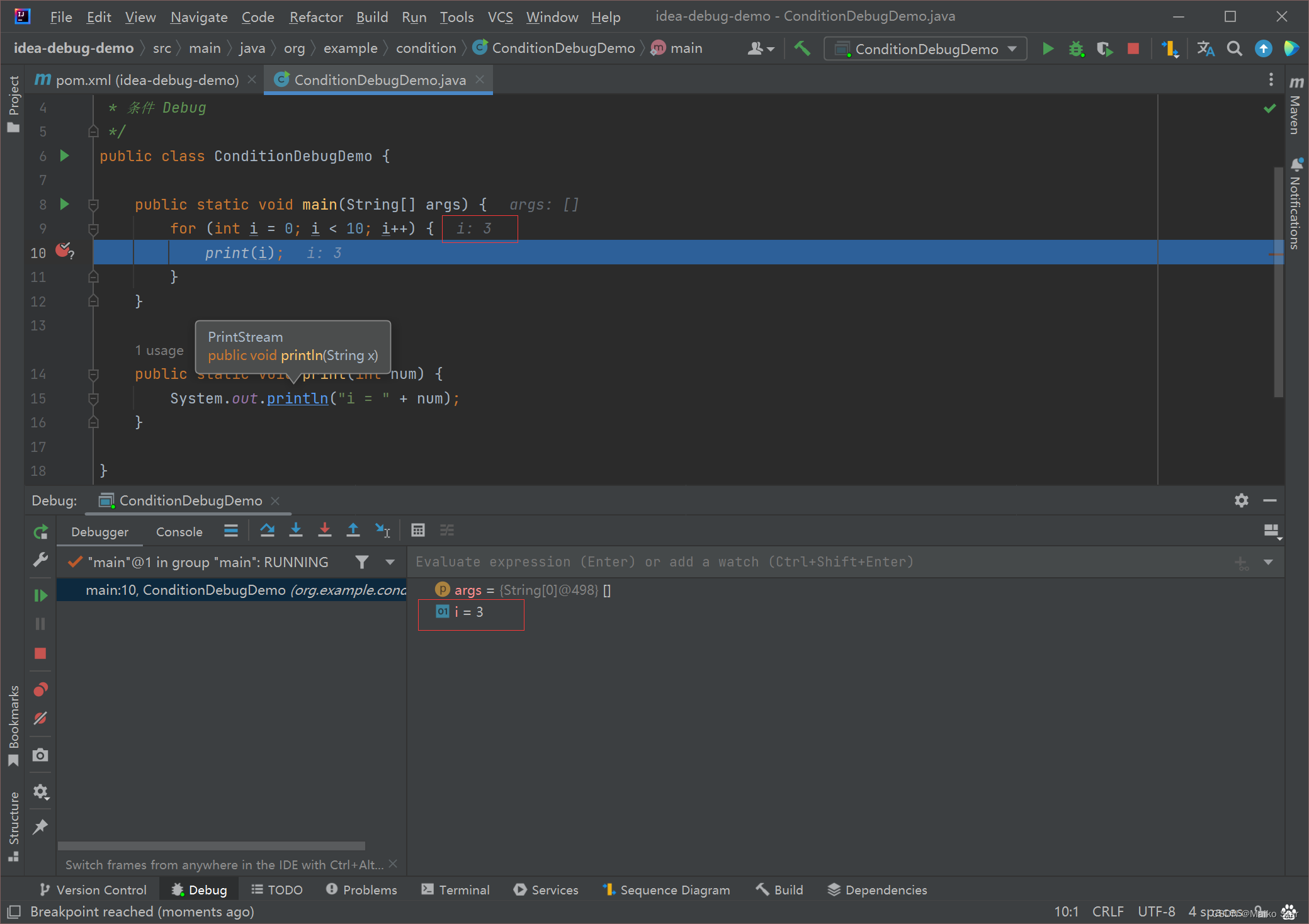
在acwing的算法基础课中，yxc给出了二分的两个模板，这里举有序数组查找某个数的例子来说明这两个模板。

模板1：

当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid +1;，计算mid时不需要加1。
此操作用于check条件是获取右半部分的第一个元素。

int bsearch_1(int l, inr r){
    while(l<r){
        int mid = l+r>>1;
        if (check(mid)) r=mid;
        else l=mid+1;
    }
    return l;
}

模板2：

当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l =mid;，此时为了防止死循环，计算mid时需要加1。
此操作用于获得左半部分的最后一个元素。

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

比如我们有一个有序数组，我们需要找到6的位置，我们可以将数组划分为两个部分，前半部分是小于6的部分，后半部分是大于等于6的部分，那么我们就有两种check的实现方式，分别对应取左半部分的最后一个<=6和取右半部分>=6的第一个：

1. a[mid]>=6
   此时check函数对应第二部分，即原数组中>=6的部分。
   检查mid是否大于等于6，即我们需要获得第二部分中的第一个元素，其就是最终的答案。
   此时使用第一个模板

#include<iostream>
#include<vector>
using namespace std;

int main(){
	vector<int> a = {1,2,3,4,5,6,7,8,9};
	int l = 0;
	int r = a.size();
	while(l < r){
		int mid = (l + r)>>1;
		if(a[mid] >= 6) r = mid;
		else l = mid + 1;
	}
	cout << l;
	return 0;
} 

2. a[mid]<=6
   此时check函数对应第一部分，即原数组中<=6的部分。
   检查mid是否小于等于6，即我们需要获得第一部分中的最后一个元素，其就是最终的答案。
   此时使用第二个模板

#include<iostream>
#include<vector>
using namespace std;

int main(){
	vector<int> a = {1,2,3,4,5,6,7,8,9};
	int l = 0;
	int r = a.size();
	while(l < r){
		int mid = (l + r + 1)>>1;
		if(a[mid] <= 6) l = mid;
		else r = mid - 1;
	}
	cout << l;
	return 0;
} 

为什么第二个模板需要l+r+1/2
因为如果r=l+1的时候，不+1的话mid就会等于l，如果进入check条件就会进入死循环。