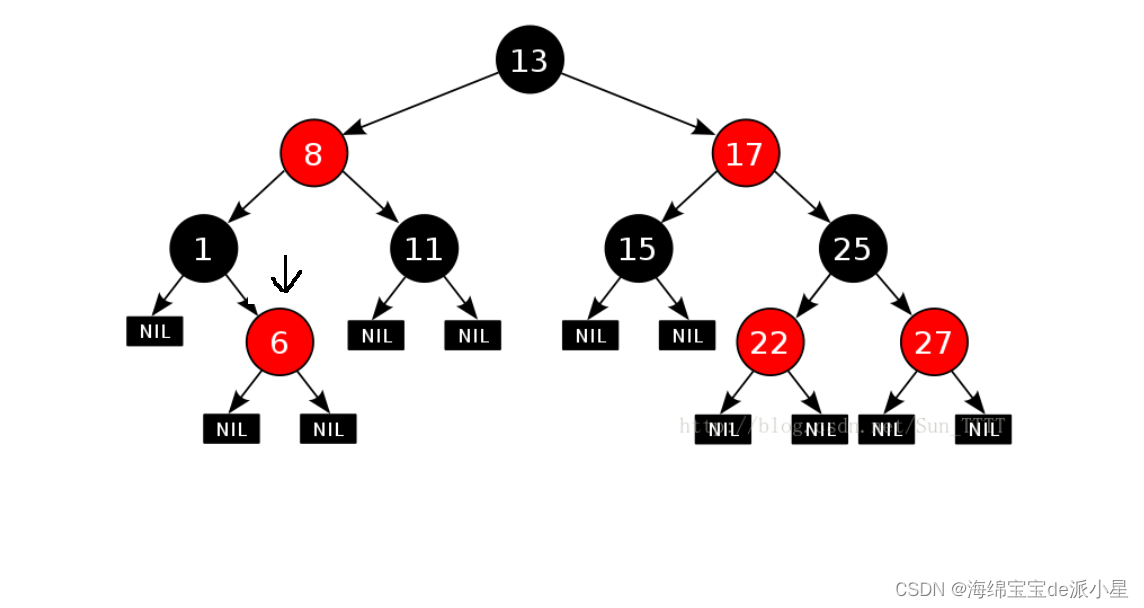
单调栈解决的问题
我们单调栈的提出主要是为了解决这么一个问题
现在给我们一个数组 现在要求你建立一张表 这张表中能够查询到两个信息
这两个信息分别是
- 当前数字左边小于该数字并且下标位置最相近的下标
- 当前数字右边小于该数字并且下标位置最相近的下标
同理 大于也可以
原本我们暴力的方法是每次遍历到需要知道前后下标的位置我们都往前或者是往后遍历出我们需要的数据 这样子的时间复杂度就是N平方
而我们单调栈的方法能做到 N 的时间复杂度
整体思路(无重复值版)
单调栈解决上面问题得思路如下
我们首先要准备一个空的栈 我们要确保这个栈从栈底到栈顶的数字由小到大
假设我们现在有一个数组 【3 ,4 ,2,6,1,7,0】
- 此时由于栈里面没有数据我们的元素3 直接入栈 到下一个元素4
- 此时由于栈里面的元素3 小于我们的元素4 符合规则 所以说元素4直接入栈 到下一个元素2
- 此时由于栈里面的元素4 大于要插入的元素2 不符合规则 所以说元素4要出栈
- 而在元素4出栈的一瞬间我们也就得到了我们需要的一组数组
- 小于元素4并且位于左侧的数是3 小于元素4并且位于右侧的数是2
- 后面的数据以此类推 … …
原理解释
- 为什么栈下面的元素就是距离当前元素左侧最近的且小于当前数字的数
因为我们栈是严格按照从小到大的顺序进行排列的 所以说下面的元素一定小于当面的元素 所以说小于当前数字证明完毕
如果说还有其他元素距离当前元素的左侧更近并且小于当前元素 那么这个元素一定会出现在栈中这两个元素的中间
- 为什么还未入栈的元素就是距离当前元素右侧最近且小于当前数字的数
因为我们栈是严格按照从小到大的顺序进行排列的 所以说只有比当前元素小的元素才能让当前元素出栈
如果说还有其他元素是距离当前元素的右侧更近并且小于当前元素 那么这个元素一定提前让当前元素出栈
整体思路(有重复值版)
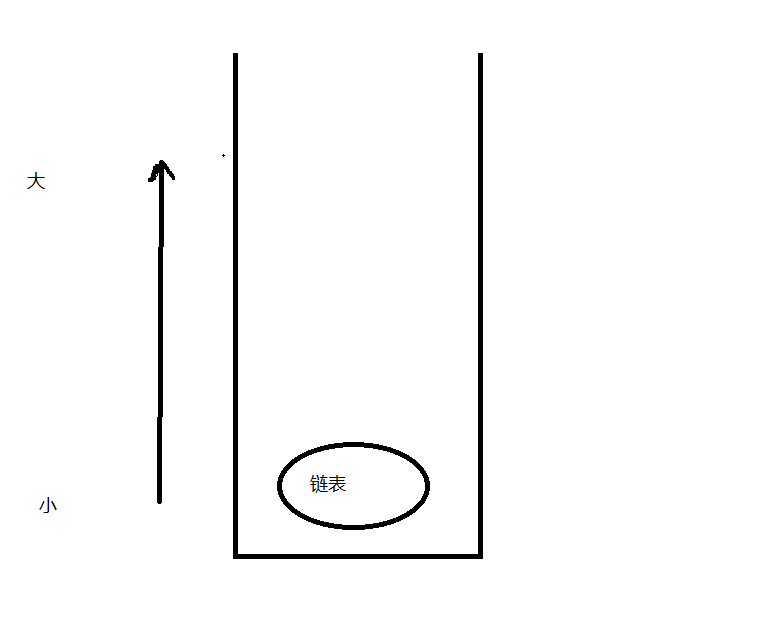
有重复值版本和无重复值版本最主要的一个区别就是 有重复值版本里面存放的元素是一个链表 该链表连接着各个元素值相同的元素的下标
- 寻找距离当前元素右侧最近并且小于该元素的值的元素步骤和无重复值一样
- 寻找距离当前元素左侧最近并且小于该元素的值的元素时 如果下次是一个链表 则我们要选择这个链表的最后一个元素
代码表示(默认全部数字为正整数)
有重复值版
函数表示如下
vector<vector<int>> MonotonicStack(vector<int>& arr);
返回值说明
我们返回的是一个二维数组
该二维数组的下标对应着数组中数字的下标 二维数组中的每一行有两个元素 这两个元素分别代表着距离当前元素左边(右边)最近的且小于当前元素的值 如果不存在该值 则填入 -1
参数说明
一个一维数组
无重复版代码表示如下
vector<vector<int>> MonotonicStack(vector<int>& arr)
{
int N = static_cast<int>(arr.size());
vector<vector<int>> ans(N , vector<int>(2 , -1));
stack<int> st;
for (int i = 0; i < N; i++)
{
while(!st.empty() && arr[st.top()] > arr[i])
{
int PopIndex = st.top();
st.pop();
int LeftIndex = st.empty() ? -1 : st.top();
ans[PopIndex][0] = LeftIndex;
ans[PopIndex][1] = i;
}
st.push(i);
}
// 此时栈中还有剩余元素未清空
while (!st.empty())
{
int PopIndex = st.top();
st.pop();
int LeftIndex = st.empty()? -1 : st.top();
ans[PopIndex][0] = LeftIndex;
ans[PopIndex][1] = -1; // 这里也可以不写 因为本来就是-1
}
return ans;
}
有重复值版
函数表示如下
vector<vector<int>> MonotonicStack(vector<int>& arr);
返回值说明
我们返回的是一个二维数组
该二维数组的下标对应着数组中数字的下标 二维数组中的每一行有两个元素 这两个元素分别代表着距离当前元素左边(右边)最近的且小于当前元素的值 如果不存在该值 则填入 -1
参数说明
一个一维数组
有重复值版代码表示如下
vector<vector<int>> MonotonicStack(vector<int>& arr)
{
int N = static_cast<int>(arr.size());
vector<vector<int>> ans(N , vector<int>(2 , -1));
stack<list<int>> st;
for (int i = 0; i < N ; i++)
{
while(!st.empty() && arr[st.top().front()] > arr[i])
{
list<int> popIs = st.top();
st.pop();
int LeftIndex = st.empty() ? -1 : st.top().back();
// 之后依次更新该链表中的所有位置
for (auto x : popIs)
{
ans[x][0] = LeftIndex;
ans[x][1] = i;
}
}
if (!st.empty() && arr[st.top().front()] == arr[i])
{
st.top().push_back(i);
}
else // empty || <
{
list<int> Ins = {i};
st.push(Ins);
}
}
// 更新完毕之后可能栈里面还有值 也要全部更新完毕 最后返回ans
while(!st.empty())
{
list<int> popIs = st.top();
st.pop();
int LeftIndex = st.empty() ? -1 : st.top().back();
// 之后依次更新该链表中的所有位置
for (auto x : popIs)
{
ans[x][0] = LeftIndex;
ans[x][1] = -1;
}
}
return ans;
}
单调栈相关题目
题目一
给定一个只包含正数的数组arr , 该数组中的任意一个子数组sub 都会有一个A指标
A指标的计算方法为 (sub数组的和)* (sub数组中的最小值)
现在要求你设计一个函数 返回arr中所有子数组中最大的A指标
注意 子数组是连续的
解题思路
解决这个问题的思路其实很简单 假设我们目前有一个数组 arr 其中A指标最大的子数组是sub
那么sub中的最小值是不是肯定是数组arr的一个数字
既然我们确定了最小值 A指标的计算公式又是 最小值 * (sub数组和)
那么我们是不是只要让以该下标作为最小值的子数组尽可能的大就好了啊
那么现在的问题就转化为了 怎么才能让这个子数组尽可能的大呢?
一个比较笨的办法就是依次往左往右遍历嘛 但是这样子时间复杂度就会很高
还有一种方式就是按照我们写的单调栈 只需要将ans数组中的下标加一减一就好了(边界问题需要自己考虑)
关于数组和的计算我们可以使用前缀和数组来简化
代码表示如下
vector<int> arr = {3 , 1, 1 ,3 , 5, 5, 5};
vector<vector<int>> ans = MonotonicStack(arr);
int N = static_cast<int>(arr.size());
// 前缀和数组
vector<int> prearr(N , 0);
prearr[0] = arr[0] ;
for(int i = 1; i < N; i++)
{
prearr[i] = prearr[i - 1] + arr[i];
}
vector<int> max_ans(N , 0);
// 以数组的每个位置作为最小值 尽可能扩大数组范围 计算出结果 最后结果就在其中
for (int i = 0; i < N; i++)
{
int LeftIndex = ans[i][0] == -1 ? 0 : ans[i][0] + 1;
int RightIndex = ans[i][1] == -1 ? N - 1 : ans[i][1] - 1;
int sub_sum = prearr[RightIndex] - prearr[LeftIndex] + arr[LeftIndex];
max_ans[i] = sub_sum * arr[i];
}
之后max_ans数组里面的结果就是最终答案
题目二
给定一个非负数组 arr 代表直方图 返回直方图的最大长方形面积
题目解释
直方图的含义如下 以数组 【3 , 2,4 ,2 , 1】为例 如下图
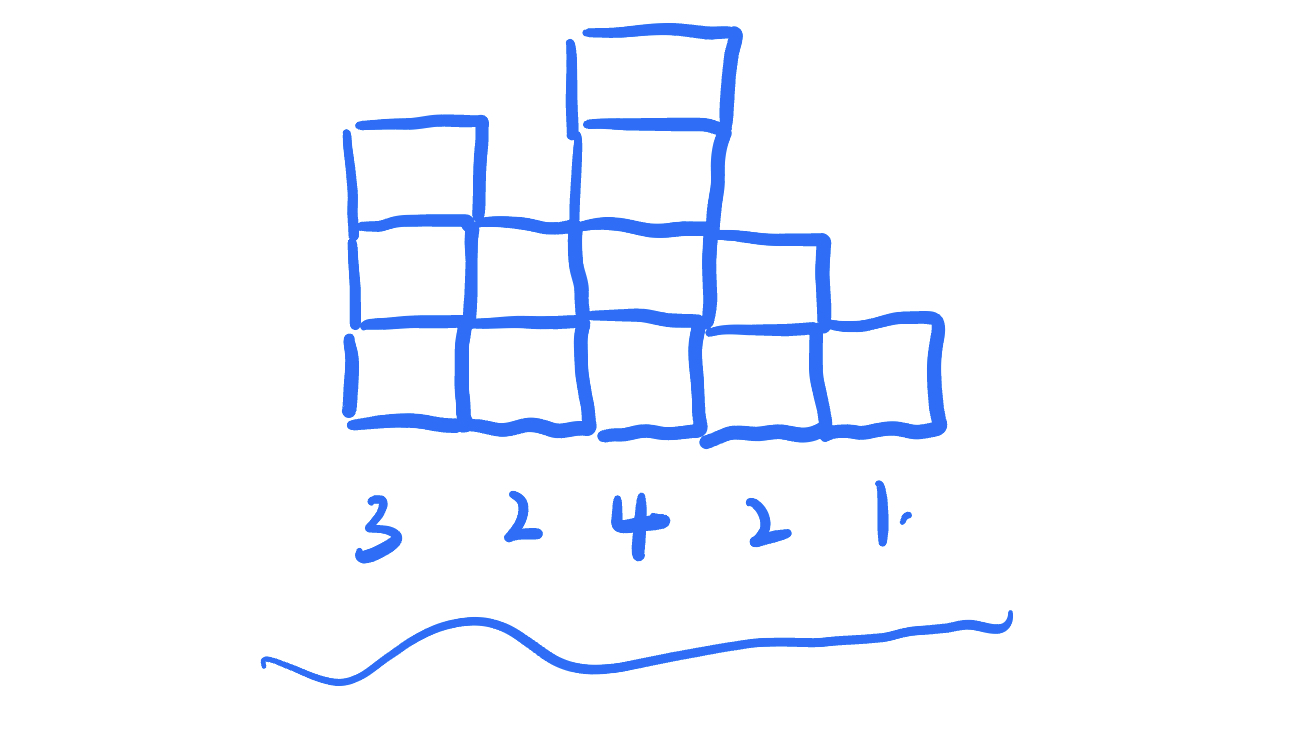
每个下标代表着当前位置的告诉 最终他们组成了一个图形
现在要你求这个图形中 最大的长方形面积
解题思路
其实这个问题和上个问题的思路完全一致
我们只需要遍历数组中每一个元素 然后尽可能的让这个长方形变大即可
代码类似于题目一 这里就不提供了
题目三
给定一个二维数组 matrix 其中的值不是0就是1
返回由1组成的一个最大子矩阵 给出其中1的数量
题目解释
给出一个二维数组图 matrix

我们的子矩阵中只能包含1 现在要求你在图中找出一个最大的子矩阵 并且返回1的个数
解题思路
如果我们使用纯暴力的方法去解这道题的话 它的时间复杂度就是N的四次方
(计算方式为 我们在二维表中任意选一点的时间复杂度为n平方 而两点可以组成一个矩阵 所以说时间复杂度为n的四次方)
我们正常的解题思路如下
既然要求的是在matrix中的一个子矩阵 那么该矩阵的 “地基”是不是肯定是matrix中的某一行啊
那么只要我们依次算出以matrix中每一行作为地基时最大的矩阵即可
代码思路
我们以matrix的列数为大小创建一个数组
该数组中更新以每行作为地基时的直方图 以下图为例 更新的直方图数组为

1 1 1 0 1
0 2 2 1 0
1 3 3 2 1
2 4 0 0 2
0 0 1 1 3
1 1 0 0 4
2 2 0 0 5
接下来的问题就转化为了计算上面这些直方图中矩形面积的最大值 类似题目二