6.6二叉树的最大深度（LC104-E）、N叉树的最大深度（LC559-E）

news2024/7/4 4:28:16

二叉树的最大深度：

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

二叉树的最大深度=二叉树的高度

算法：

这道题既可以求深度，也可以直接求高度。不过高度和深度用的遍历方式不同。

二叉树写代码之前要确定遍历顺序！

求高度（从下往上求高度）：后序遍历（左右中）。先求左右孩子的最大高度（左右），再加上根节点的高度（中）。

求深度：前序遍历（中左右）。

调试过程:

递归法：

原因：node可能为空，我没判断node非空

正确代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root == None:
            return 0
        else:
            return self.getdepth(root)

    def getdepth(self,node:Optional[TreeNode])-> int:
        if node == None:
            return 0
        else:
            #左右
            leftheight = self.getdepth(node.left)
            rightheight = self.getdepth(node.right)
            #中
            depth = 1+max(leftheight,rightheight)
            return depth

时间空间复杂度：

时间复杂度： 该代码使用递归方法计算二叉树的最大深度。在最坏的情况下，当二叉树完全不平衡并且类似于链表时，代码将恰好访问每个节点一次。因此，代码的时间复杂度为O(n)，其中n是二叉树中的节点数。
空间复杂度： 代码的空间复杂度由二叉树的最大深度决定。在最坏的情况下，当二叉树完全不平衡并且类似于链表时，最大深度（高度）将等于树中的节点数。因此，代码的空间复杂度为O(n)，其中n是二叉树中的节点数。
总体而言，该代码的时间复杂度为O(n)，空间复杂度为O(n)。

N叉树的最大深度：

算法：

求高度（从下往上求高度）：先求根节点所有子树的最大高度，再加上根节点的高度。

N叉树的定义（要会写！）：

class Node:
    def __init__(self, val=None, children=None):
        self.val = val
#children就是根节点的孩子
        self.children = children

调试过程：

递归法：

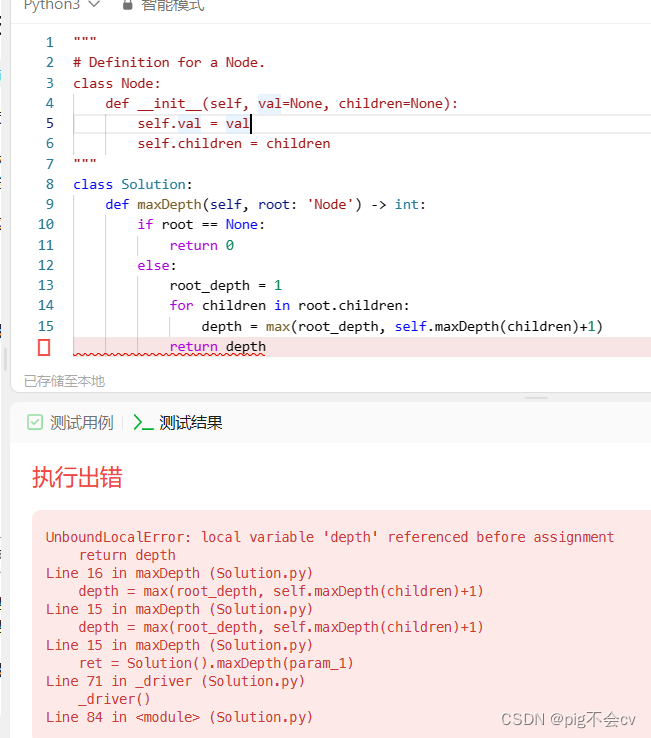
原因：

错误是在 `for` 循环中尝试使用变量 `depth`，但在循环之前没有初始化该变量。这导致在 `return depth` 语句处引发了 `UnboundLocalError` 错误。

要解决这个问题，可以在 `maxDepth` 方法之前初始化 `depth` 变量

正确代码：

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""
class Solution:
    def maxDepth(self, root: 'Node') -> int:
        if root == None:
            return 0
        else:
            depth = 1
            for children in root.children:
                depth = max(depth, self.maxDepth(children)+1)
            return depth