代码随想录算法训练营第五十三天 | LeetCode 1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和
文章链接:最长公共子序列、不相交的线、最大子数组和
视频链接:最长公共子序列、不相交的线、最大子数组和
1. LeetCode 1143. 最长公共子序列
1.1 思路
-
在718. 最长重复子数组中的重复子数组要求是连续的,本题也是要求重复子数组,要按照数组的顺序,虽然可以不连续。本题用动态规划解决的难点在于如何去表示这两个数组进行比较的状态,在718. 最长重复子数组中我们是用二维数组比较的,横向表示 nums1,纵向表示 nums2
-
dp 数组及其下标的含义:dp[i][j]:长度以 [0,i-1] 的 nums1 和长度以 [0,j-1] 的 nums2 的最长公共子序列为 dp[i][j]。为什么定义 i-1 而不是 i 呢?其实也可以,但是那么写可以精简一些初始化的地方,如果写成 i 就需要对第一行和列初始化
-
递推公式:我们肯定要比较元素是否相同,即 if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1,就是在这基础上加 1。如果不相同,即 else dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j])

-
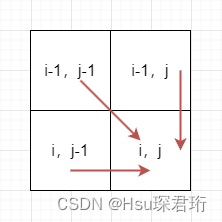
dp 数组的初始化:从递推公式可看出,i,j 是需要这三个方向推导出来的,因此要把第一行和列初始化了,即 dp[0][j] 和 dp[i][0],那么根据 dp 数组的含义,是跟 [0,i-1] 和 [0,j-1] 比较,本来就是 0 了再减 1 就成负的,就是一个空的字符串的,那么即 nums1 和空的字符串的最长公共子序列以及 nums2 和空的字符串的最长公共子序列就应该是 0,因此都初始化为 0。而其余下标会被其他位置覆盖,就也初始化为 0 即可
-
遍历顺序:根据上图的方向,因此是从左往右遍历。for(int i=1;i<=nums1.length;i++)for(int j=1;j<=nums2.length;j++)为什么从 1 开始,因为第一行和列都初始化了,并且递推公式也是从 i-1 和 j-1 推导来的,因此从 1 开始,为什么需要等于号,因为根据 dp 数组的含义,我们的数组范围是 [0,i-1] 和 [0,j-1],只有去等于号了,才能取到数组的最后一个元素,而我们定义 dp 数组时也应该定义个长度为 nums1.length+1,nums2.length+1。最终结果存在 dp[nums1.length][nums2.length]
-
打印 dp 数组:用于 debug
1.2 代码
/*
二维dp数组
*/
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
// char[] char1 = text1.toCharArray();
// char[] char2 = text2.toCharArray();
// 可以在一開始的時候就先把text1, text2 轉成char[],之後就不需要有這麼多爲了處理字串的調整
// 就可以和卡哥的code更一致
int[][] dp = new int[text1.length() + 1][text2.length() + 1]; // 先对dp数组做初始化操作
for (int i = 1 ; i <= text1.length() ; i++) {
char char1 = text1.charAt(i - 1);
for (int j = 1; j <= text2.length(); j++) {
char char2 = text2.charAt(j - 1);
if (char1 == char2) { // 开始列出状态转移方程
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[text1.length()][text2.length()];
}
}
2. LeetCode 1035. 不相交的线
2.1 思路
- 本题要在两个数组中找到相同的数字然后连成线,并且线之间不能相交。本题很容易陷进去怎么判断线不能相交的问题。我们要找的是相同元素,同时保证数组顺序不变,其实也是求子序列问题。举例如果两个数组是 [1,2][2,1] 那这是相同子序列吗?不是,这里相同子序列只能是 1 和 1 或者 2 和 2。那本题让我们找最多条可连接的线,就相当于找最长公共子序列,那和1143. 最长公共子序列就一样了。
- 因此本题的解题逻辑和我在1143. 最长公共子序列这题的是一样的。
2.2 代码
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}
3. LeetCode 53. 最大子数组和
3.1 思路
- 本题是给一个数组求最大子序和,指的就是子数组的最大和,子数组就是连续的子序列,求出和是在这个数组的子数组中最大的。本题可以暴力也可以贪心,但这里用动态规划做。
- dp 数组及其下标的含义:dp[i]:以 i 为结尾(即元素 nums[i])的最大连续子序列的和为 dp[i]
- 递推公式:有两种情况,1 是延续着前面的子序列的和继续累加;2 是不延续前面的子序列,从现在的位置重新开始算。第 1 种情况,nums[i] 前面的和就是以 i-1 为结尾的最大子序列和 dp[i-1],即 dp[i-1]+nums[i],第 2 种情况就是不要前面的了,即 nums[i]。因此 dp[i]=Math.max(dp[i-1]+nums[i],nums[i])
- dp 数组的初始化:dp[i] 是依赖 dp[i-1] 的,源头是 dp[0],因此初始化为 nums[0],即以第一个元素为结尾的最大子序列和,非 0 下标会被覆盖,因此默认初始化为 0 即可
- 遍历顺序:按照递推公式就是从前往后遍历,for(int i=1;i<nums.length;i++)从 1 开始是因为 0 位置已经初始化了,结果是整个 dp 数组的最大值,用 if(result<=dp[i])result=dp[i],而不是 dp[nums.length-1] 的位置,因为未必是以最后一个元素为结尾的最长子序列和最大。
- 打印 dp 数组:用于 debug
3.2 代码
/**
* 1.dp[i]代表当前下标对应的最大值
* 2.递推公式 dp[i] = max (dp[i-1]+nums[i],nums[i]) res = max(res,dp[i])
* 3.初始化 都为 0
* 4.遍历方向,从前往后
* 5.举例推导结果。。。
*
* @param nums
* @return
*/
public static int maxSubArray(int[] nums) {
if (nums.length == 0) {
return 0;
}
int res = nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
res = res > dp[i] ? res : dp[i];
}
return res;
}