- 任务描述
- 相关知识
- 二叉树深度概念
- 二叉树节点
- 二叉树叶子节点概念
- 编程要求
- 测试说明
任务描述
本关任务:给定一棵二叉树,计算该二叉树的深度、总节点个数和叶子节点个数。
相关知识
为了完成本关任务,你需要掌握:1.二叉树深度概念,2.二叉树节点,3.二叉树叶子节点概念。
二叉树深度概念
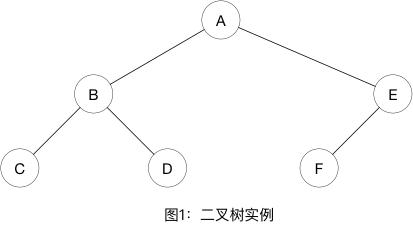
二叉树的深度指的是二叉树中最大的结点层数。例如:图1所示的二叉树最大的节点层数为3,所以该二叉树深度为3。
二叉树节点
二叉树的节点包含一个数据元素及两个指向子树的分支,例如:图1所示的二叉树的总节点个数为6。
二叉树叶子节点概念
叶子节点是度为0的节点,二叉树节点的度为子树的个数。例如:图1所示的二叉树叶子节点为C,D和F,个数为3。
编程要求
本关的编程任务是补全右侧代码片段GetTreeDepth、GetNodeNumber和GetLeafNodeNumber中Begin至End中间的代码,具体要求如下:
- 在
GetTreeDepth中计算该二叉树的深度,返回深度值。 - 在
GetNodeNumber中计算该二叉树的总的节点个数,返回节点个数。 - 在
GetLeafNodeNumber中计算该二叉树的叶子节点个数,返回叶子节点个数。
测试说明
平台将自动编译补全后的代码,并生成若干组测试数据,接着根据程序的输出判断程序是否正确。
以下是平台的测试样例:
测试输入:ABC##D##EF### 预期输出: 3 6 3
测试输入:ABCD###E#F##G## 预期输出: 4 7 3
#include "binary_tree.h"
int GetTreeDepth(BiTreeNode* root)
// 计算该二叉树的深度
// 参数:二叉树根节点root
// 返回:二叉树的深度
{
// 请在这里补充代码,完成本关任务
/********** Begin *********/
int depthval,n,m;
if (root==NULL) depthval=0;
else{
m=GetTreeDepth(root->left);
n=GetTreeDepth(root->right);
depthval=1+(m>n?m:n);
}
return depthval;
/********** End **********/
}
int GetNodeNumber(BiTreeNode* root)
// 计算该二叉树的总节点个数
// 参数:二叉树根节点root
// 返回:二叉树的总节点个数
{
// 请在这里补充代码,完成本关任务
/********** Begin *********/
int count,n,m;
if(root==NULL) count= 0;
else{
m=GetNodeNumber(root->left);
n=GetNodeNumber(root->right);
count=m+n+1;
}
return count;
/********** End **********/
}
int GetLeafNodeNumber(BiTreeNode* root)
// 计算该二叉树的叶子节点个数
// 参数:二叉树根节点root
// 返回:二叉树的叶子节点个数
{
// 请在这里补充代码,完成本关任务
/********** Begin *********/
if (root==NULL) return 0;
else if(root->left==NULL&&root->right==NULL) return 1;
else return GetLeafNodeNumber(root->left)+ GetLeafNodeNumber(root->right);
/********** End **********/
}