最大公约数

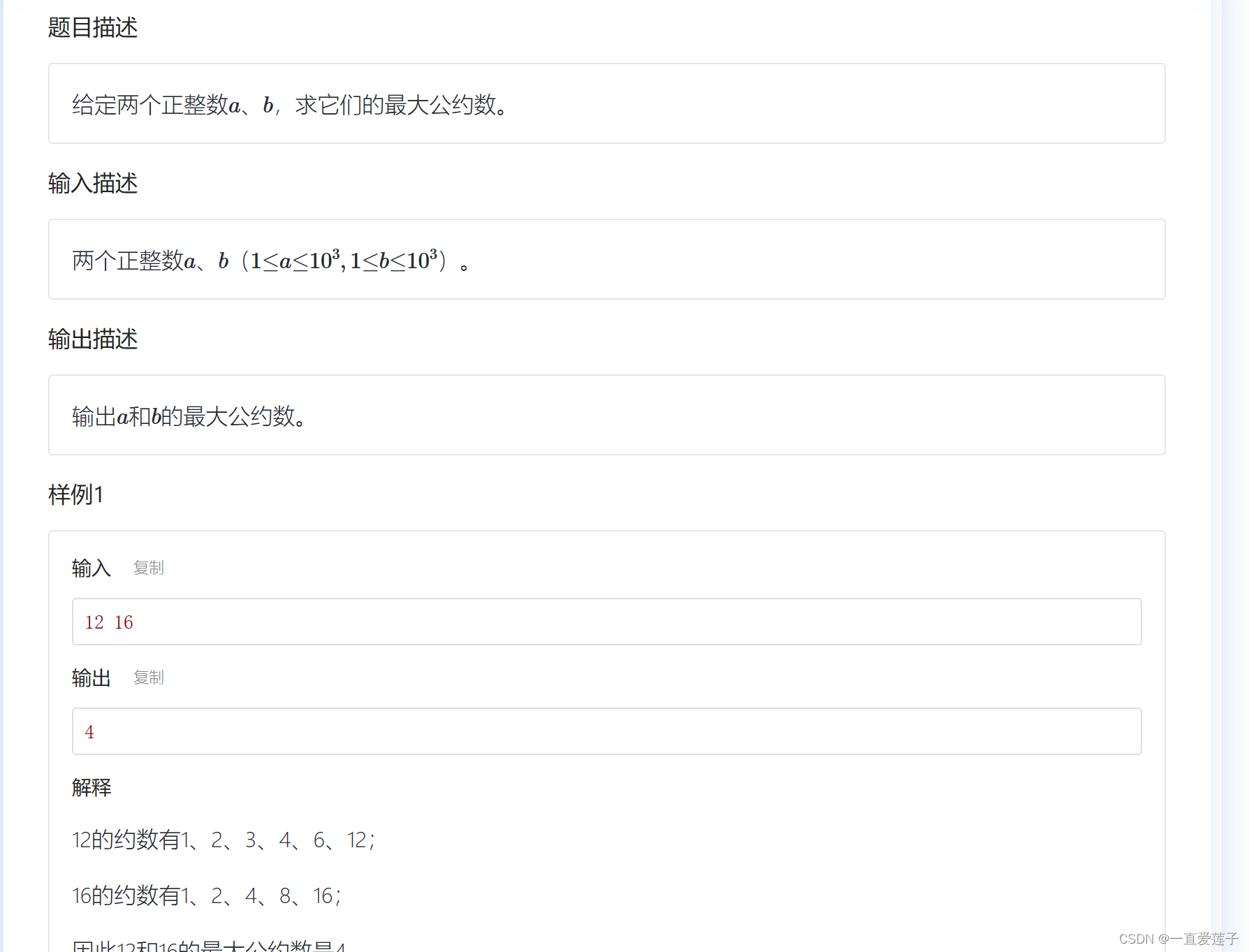
//最大公约数与最小公倍数

#include <cstdio>
int gcd(int a, int b) 
{
    if (b == 0) //截止的条件
    {
        return a;  
    }
    else   
    {
        return gcd(b, a % b);//这里是a与b和b，a%b最大公约数是相等的  
    }
}

int main()   
{
    int a, b;  
    scanf("%d%d", &a, &b);  
    printf("%d", gcd(a, b));  
    return 0;  
}

最小公倍数

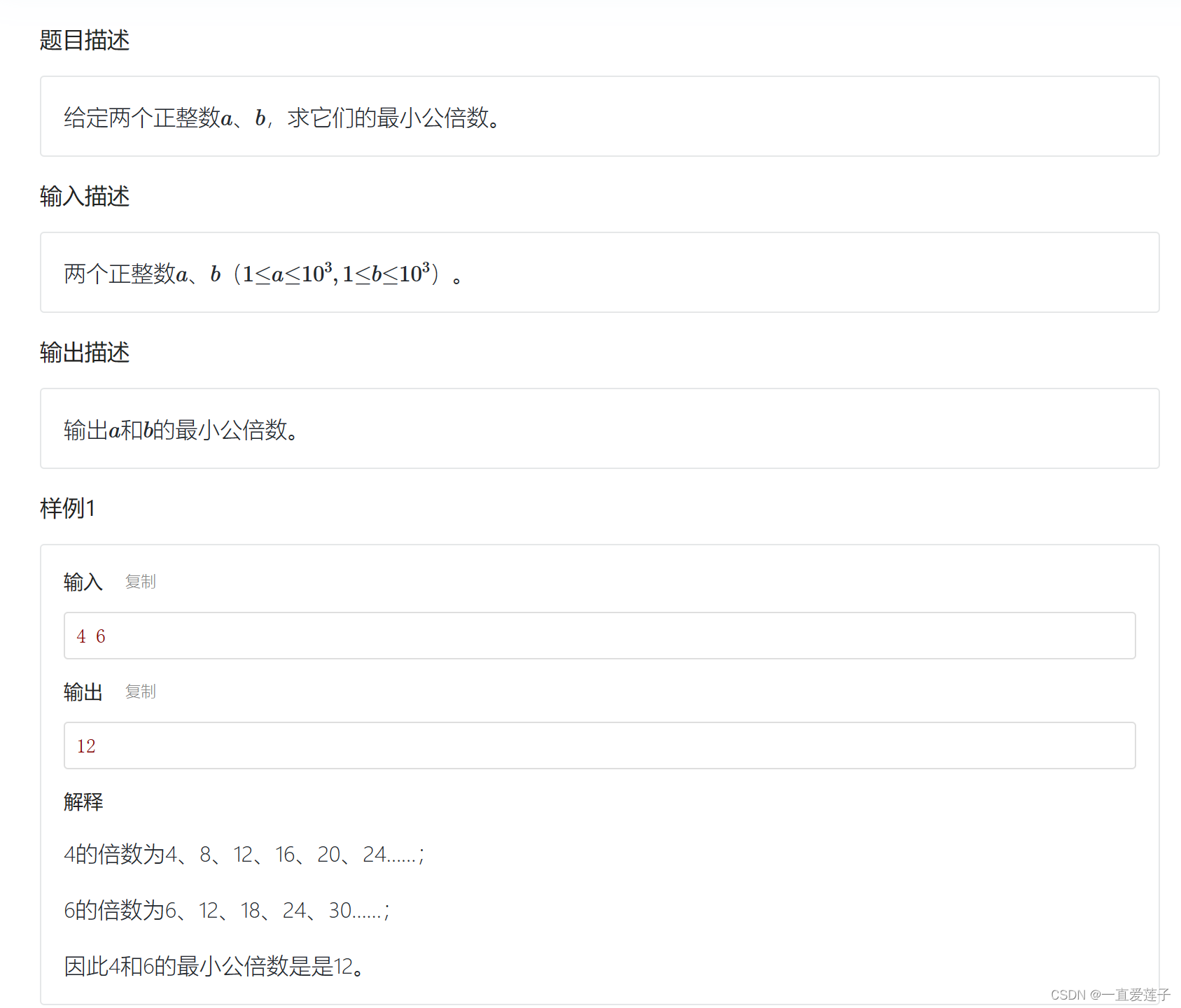
//最小公倍数是在最大公约数的上面完成的
#include <cstdio>

int gcd(int a, int b) {     
    if (b == 0) {     
        return a;     
    }
    else {     
        return gcd(b, a % b);     
    }
}

int main() {     
    int a, b;     
    scanf("%d%d", &a, &b);     
    printf("%d", a / gcd(a, b) * b);     
    return 0;     
}

最大公约数 2

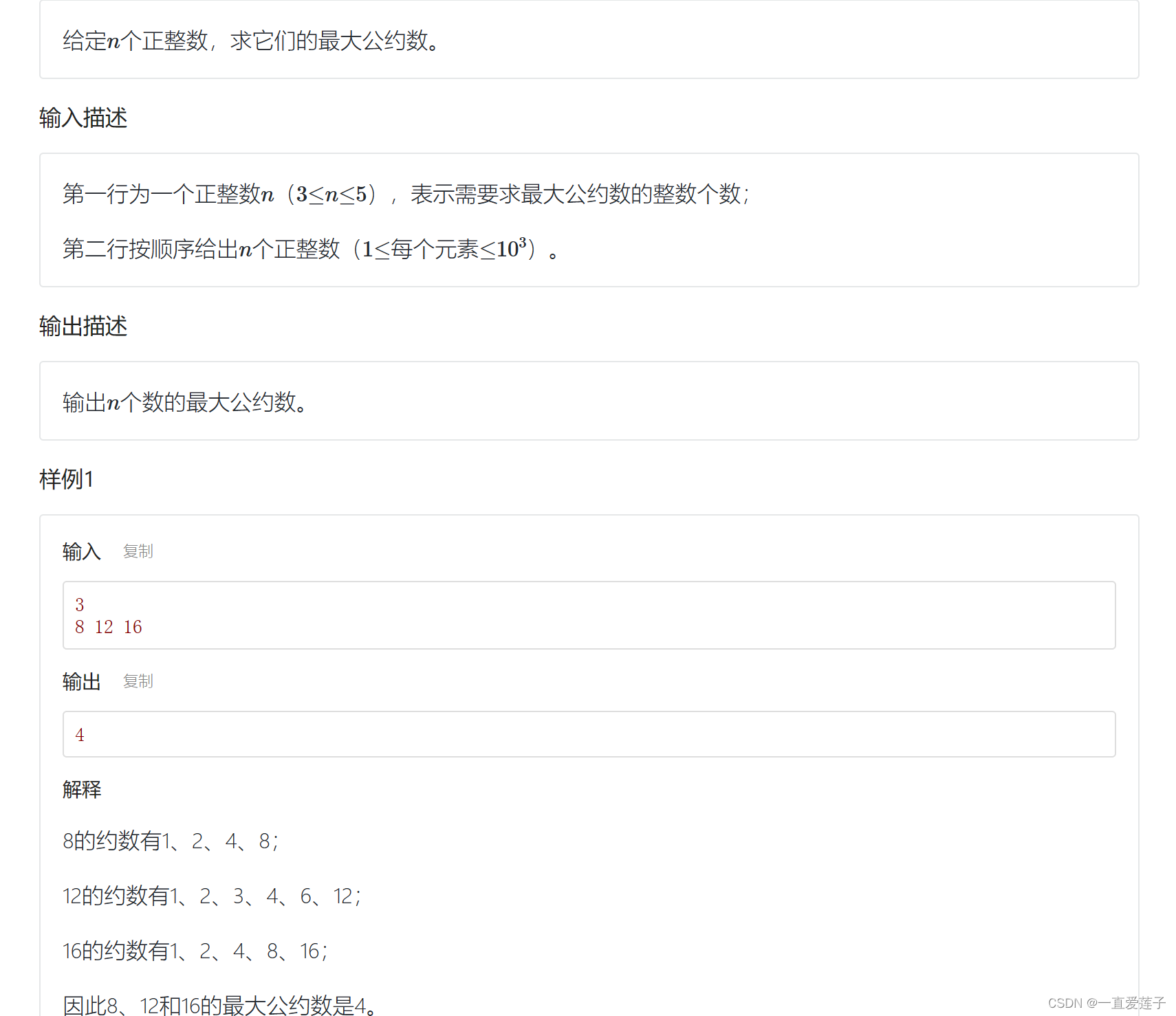
//最大公约数
#include <cstdio>
//下面还是求出的是两个数的最大公约数
int gcd(int a, int b) {
    if (b == 0) {
        return a;
    }
    else {
        return gcd(b, a % b);  
    }
}

int main() {  
    int n, x, result;  
    scanf("%d", &n);  
    scanf("%d", &result);//开始就制定一个数  
    for (int i = 0; i < n - 1; i++) {  
        scanf("%d", &x);  
        result = gcd(result, x);//这是边输出边求出两个数的最大公约数  
    }
    printf("%d", result);  
    return 0;  
}

最小公倍数2

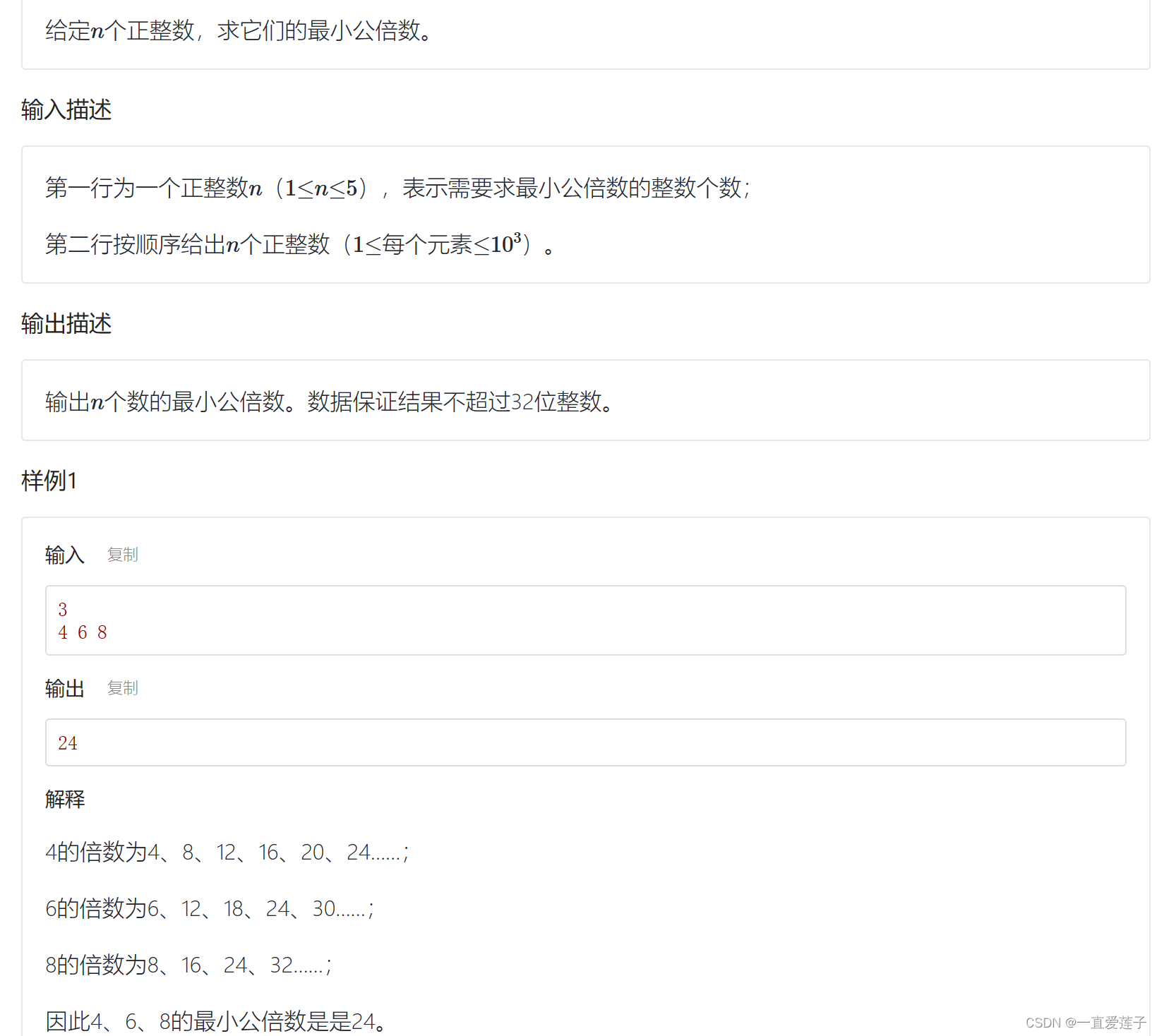
改变的思路是一样的

#include <cstdio>

int gcd(int a, int b) {
    if (b == 0) {
        return a;  
    } else {  
        return gcd(b, a % b);  
    }
}

int main() {  
    int n, x, result = 1;  
    scanf("%d", &n);  
    for (int i = 0; i < n; i++) {  
        scanf("%d", &x);  
        result = result / gcd(result, x) * x;  
    }
    printf("%d", result);  
    return 0;  
}

互质

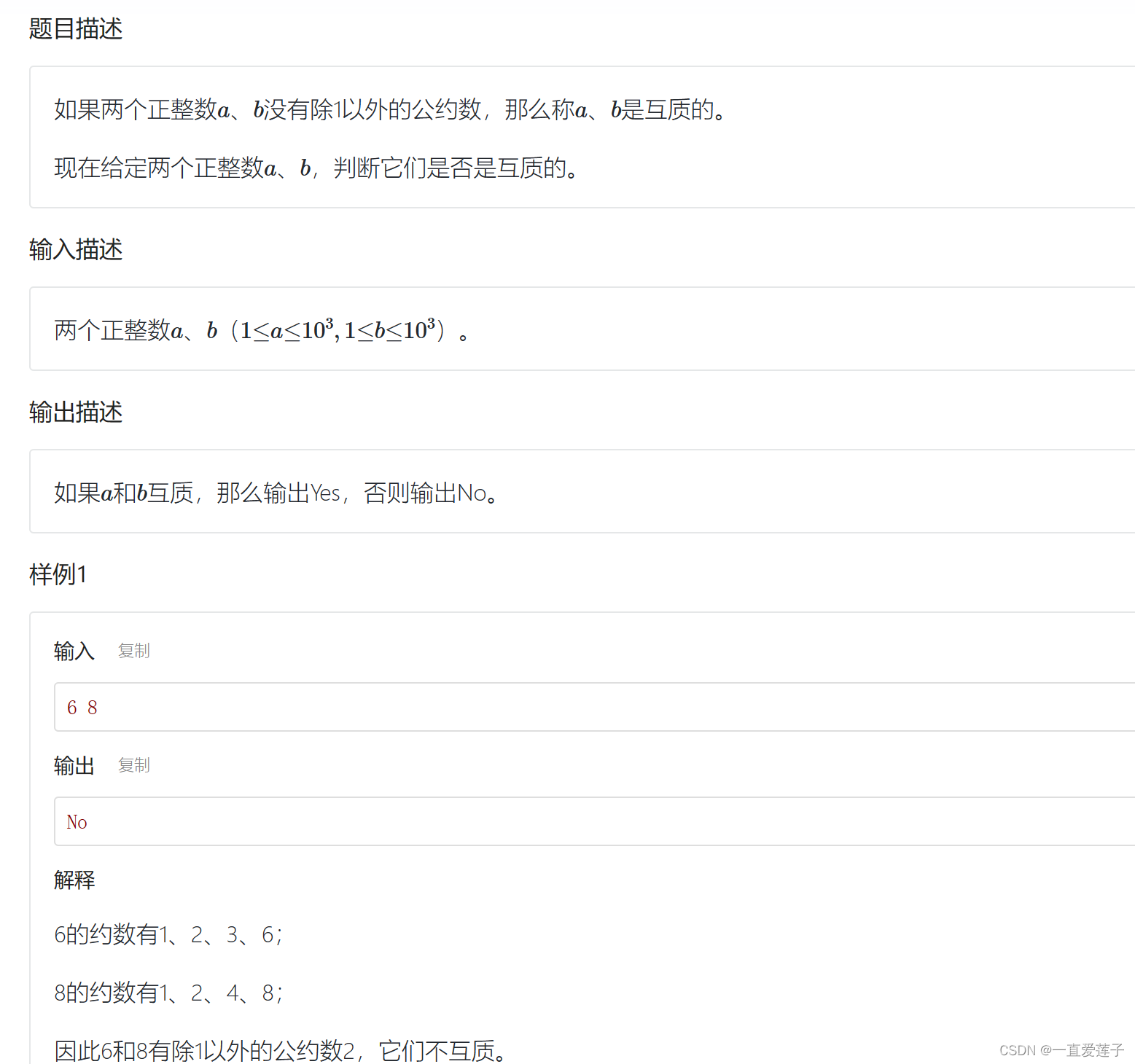
#include <cstdio>  

int gcd(int a, int b) {  
    if (b == 0) {  
        return a;  
    } else {  
        return gcd(b, a % b);  
    }
}

int main() {  
    int a, b;  
    scanf("%d%d", &a, &b);  
    printf(gcd(a, b) == 1 ? "Yes" : "No");  
    return 0;  
}

互质2

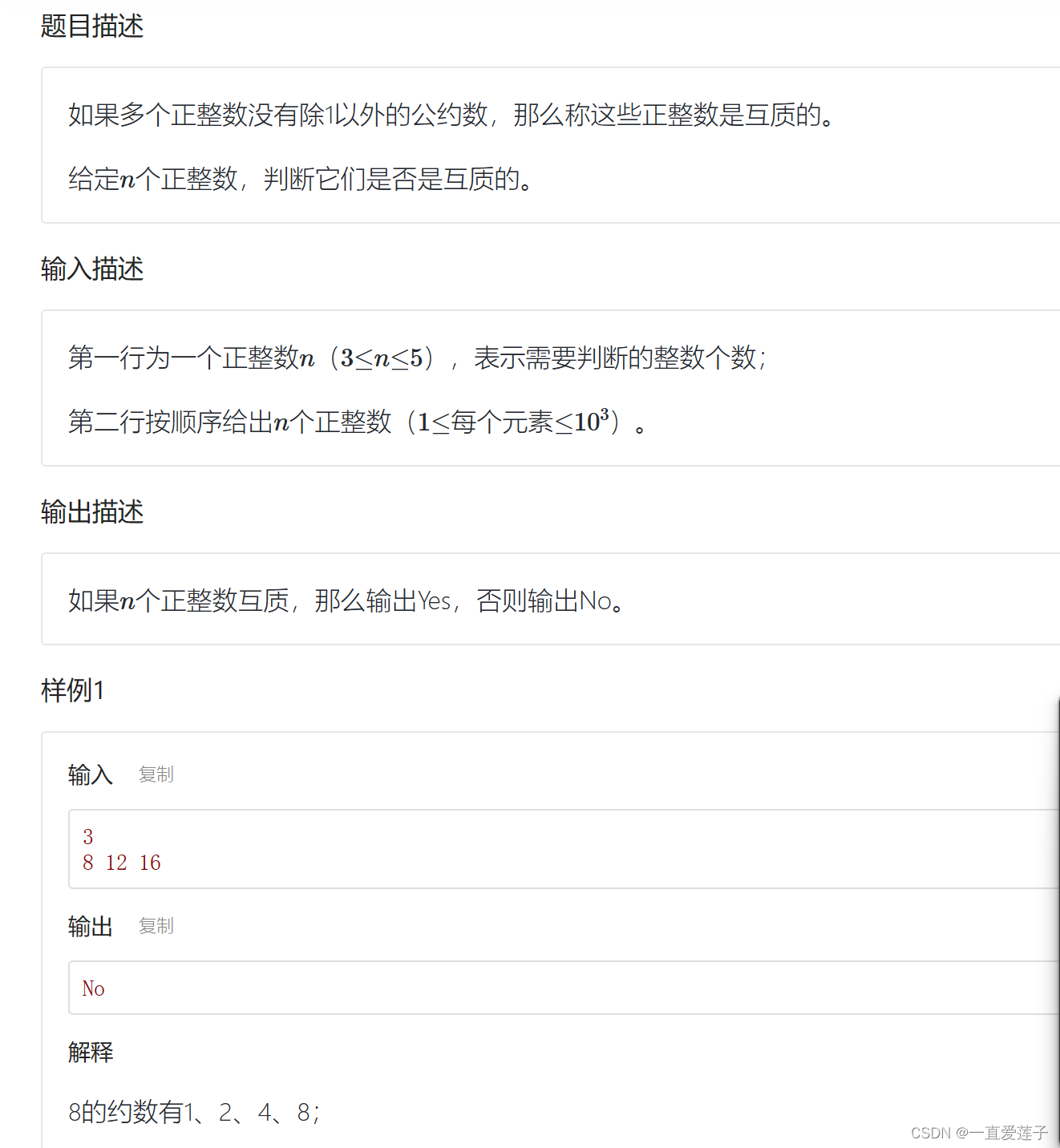
#include <cstdio>

int gcd(int a, int b) {
    if (b == 0) {
        return a;
    } else {
        return gcd(b, a % b);
    }
}

int main() {
    int n, x, result;
    scanf("%d", &n);
    scanf("%d", &result);
    for (int i = 0; i < n - 1; i++) {
        scanf("%d", &x);
        result = gcd(result, x);
    }
    printf(result == 1 ? "Yes" : "No");
    return 0;
}