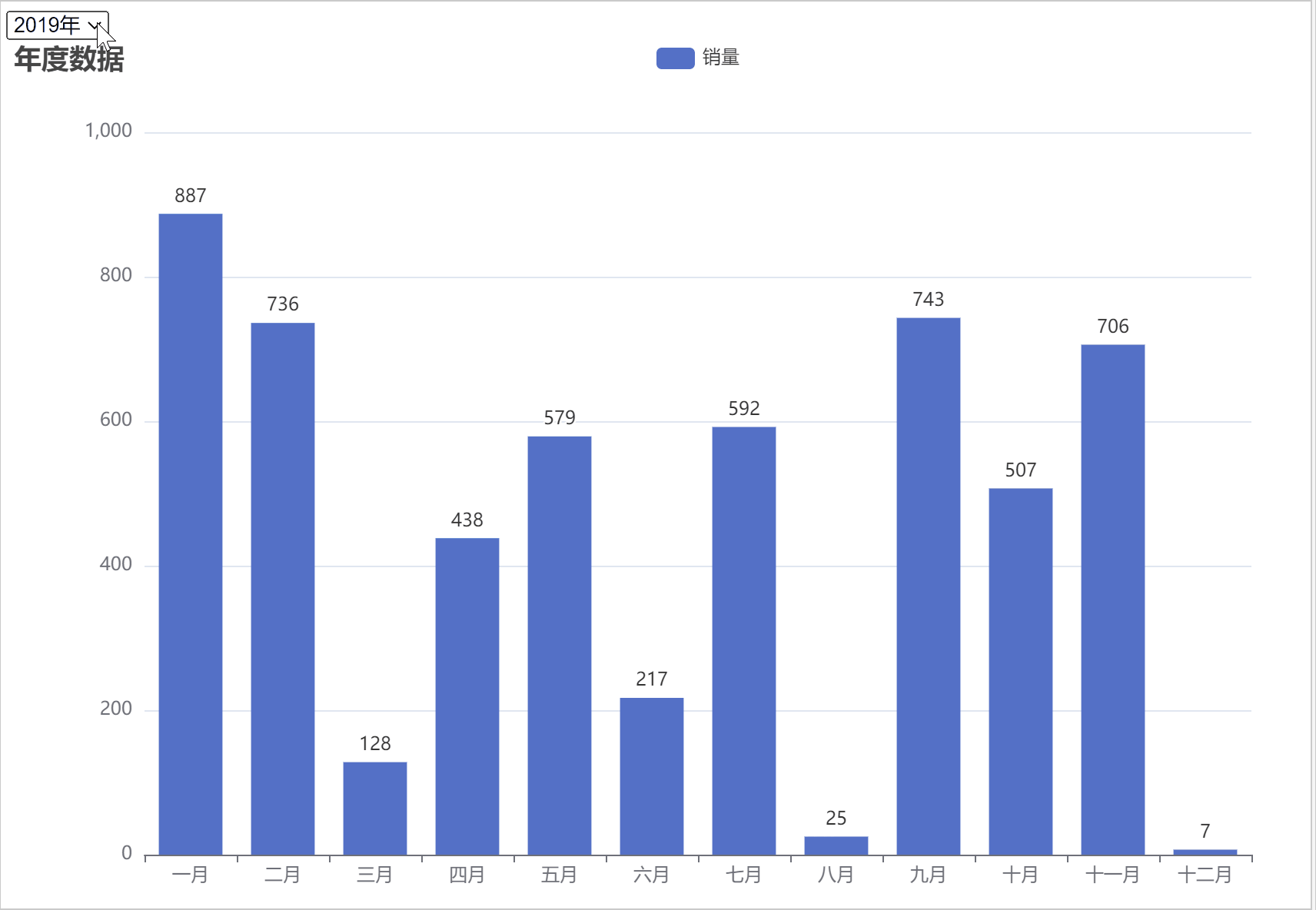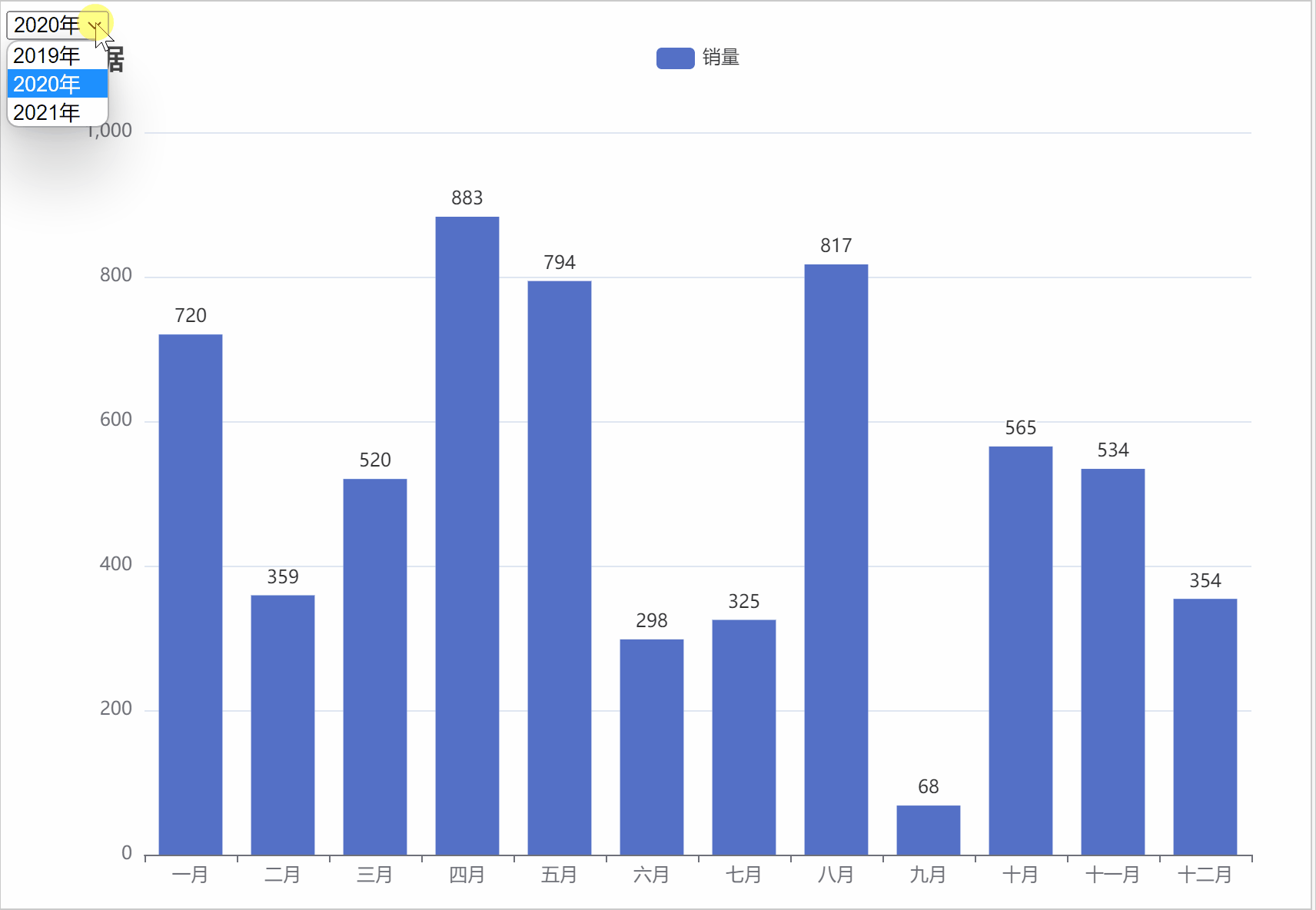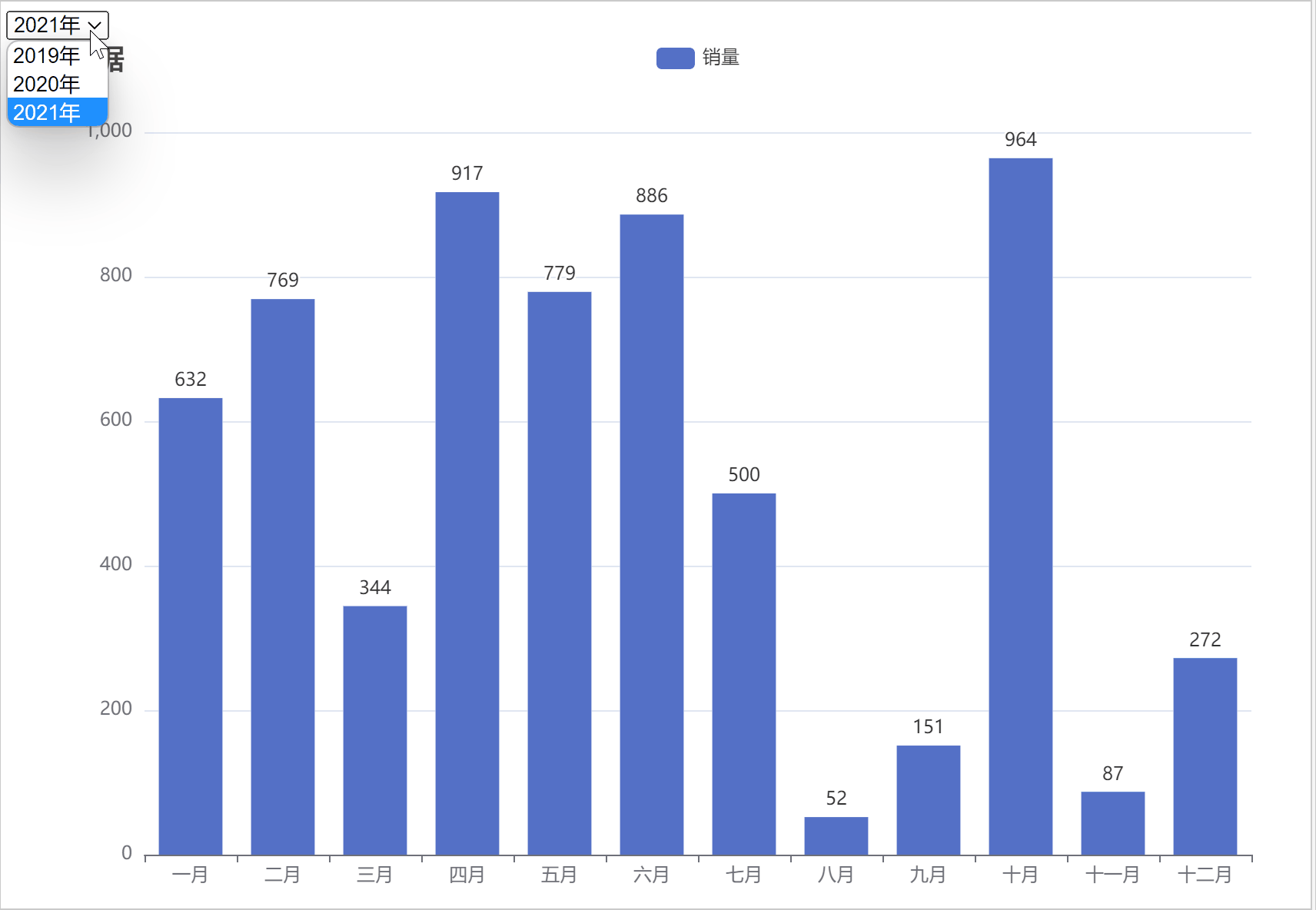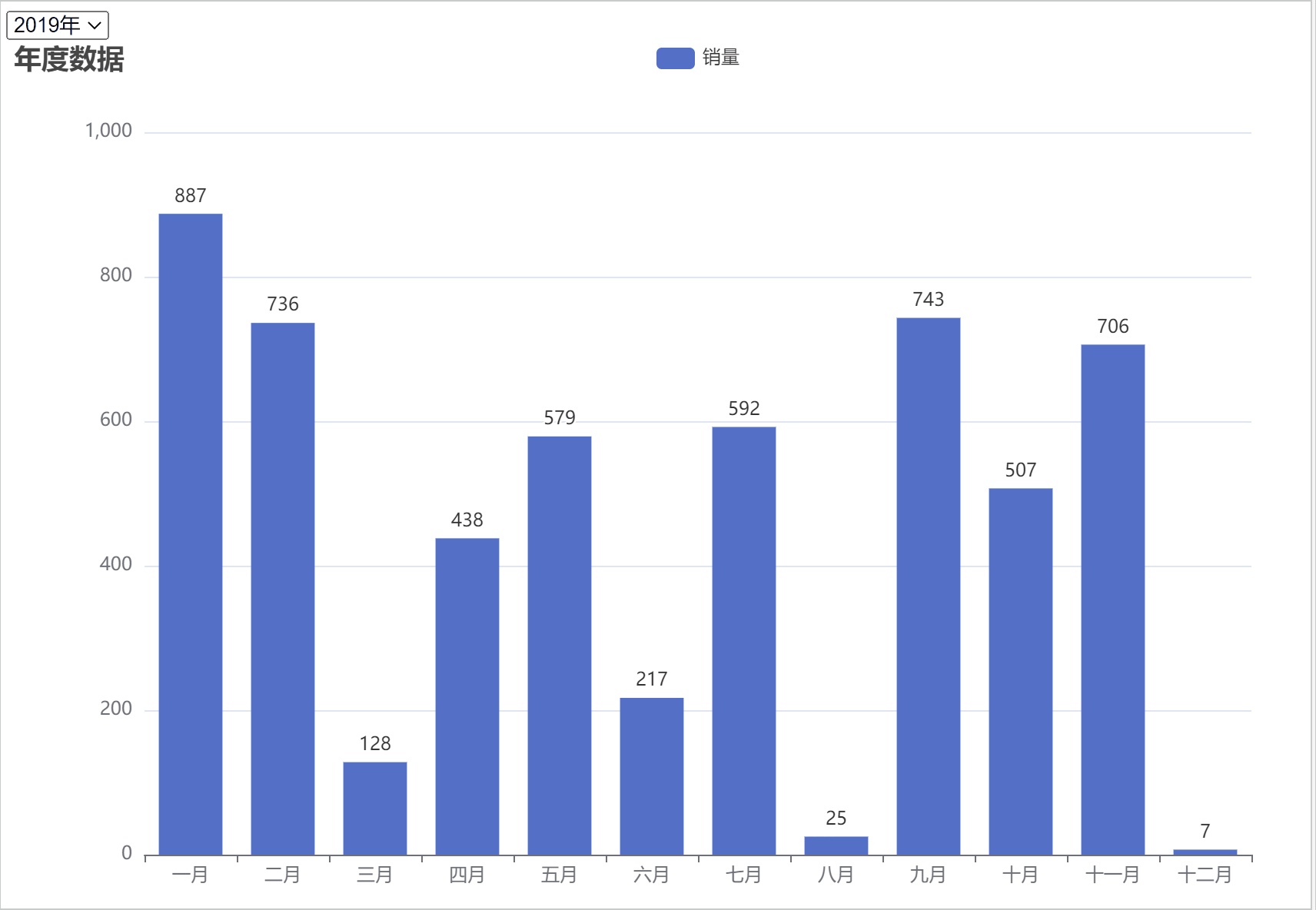
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第一篇
向量究竟是什么?
向量的线性组合,基与线性相关
矩阵与线性相关
矩阵乘法与线性变换
三维空间中的线性变换
行列式
逆矩阵,列空间,秩与零空间
克莱姆法则
非方阵
点积与对偶性
叉积
以线性变换眼光看叉积
基变换
特征向量与特征值
抽象向量空间
快速计算二阶矩阵特征值
张量,协变与逆变和秩
文章目录
- 前言
- 向量究竟是什么?
- 向量的线性组合,基于线性相关
- 矩阵与线性相关
前言
天道中丁元英说过一句话:佛说,看山是山,看水是水,普通大众寄情山水之间时,如神一般的丁元英却早已看透文化属性;今天我们不研究这么高深的哲学,回到线性代数,向量,矩阵对于我来讲只不过是一堆数字,但切换到神的视角,他们却是几何与变换,瞬间让线性代数变得更加立体生动,今天我们就从几何的角度去探索线性代数的本质。
向量究竟是什么?
通过“究竟”一词可见,对于向量的含义,存在不同的解释,目前,主要有三种解释:
⑴从物理学家的角度看:向量是指向空间的箭头,它有两个属性:长度和方向,无论怎么移动他都是同一个向量。

⑵从计算机角度看:向量是有序的数字列表,例如对于房价预测而言,房子的面积,房间数就可以看作是一个向量: [ 80 4 ] \begin{bmatrix}80\\4\end{bmatrix} [804]
⑶从数学家的角度看:向量可以是任何东西,只要具有向量和向量加法,标量和向量乘法这两种运算规律的事务都可以看作是向量
v ⃗ + w ⃗ \vec{v} +\vec{w} v+w
2 v ⃗ 2\vec{v} 2v
例如:
[
−
4
10
]
+
[
20
1
]
=
[
16
11
]
\begin{equation*} \begin{bmatrix} -4\\ 10 \end{bmatrix} +\begin{bmatrix} 20\\ 1 \end{bmatrix} =\begin{bmatrix} 16\\ 11 \end{bmatrix} \end{equation*}
[−410]+[201]=[1611]
2 ∗ [ 80 4 ] = [ 160 8 ] \begin{equation*} 2*\begin{bmatrix} 80\\ 4 \end{bmatrix} =\begin{bmatrix} 160\\ 8 \end{bmatrix} \end{equation*} 2∗[804]=[1608]
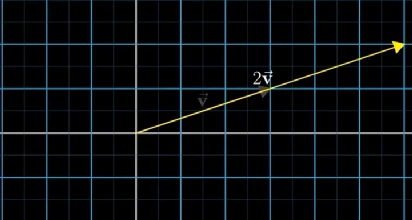
由于数学家的角度过于抽象,这就出现了开头讲的,换个角度看问题,从几何角度看待线性代数,对于向量而言,就是在特定坐标系下,以原点为起点,指向某个方向的箭头:
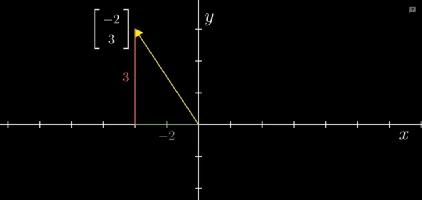
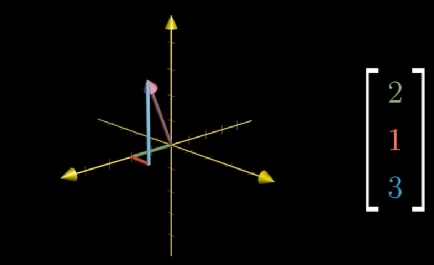
现在已经有了使用几何方式表达向量的方法,下面让我们从几何角度重新审视向量的两种运算:
对于 v ⃗ + w ⃗ \vec{v} +\vec{w} v+w而言,移动w到v的末尾,连接v的头和w的尾就是结果向量。
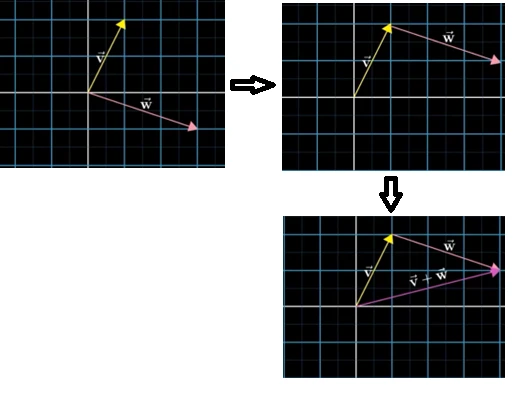
对于
2
v
⃗
2\vec{v}
2v而言,向量的方向不变,长度变为原来的两倍,如果标量是小数,则是缩小向量的长度,如果是负数,则是反方向缩放向量的长度。
向量的线性组合,基于线性相关
基向量:
“单位“是数学中必不可少的概念,缺少单位,数字变得毫无意义,同样,对于使用几何表示向量而言,也有存在单位的概念,这就是“基向量”,它代表指向x,y轴,长度为1的向量,我们分别用
i
⃗
\vec{i}
i,
j
⃗
\vec{j}
j表示。
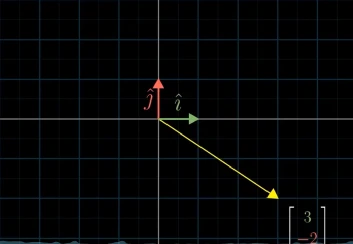
有了基的概念后,向量的表示可以转换成以基为参照,例如向量
[
3
−
2
]
\begin{bmatrix} 3\\ -2 \end{bmatrix}
[3−2],则可以表示成:
3
∗
i
⃗
+
2
∗
j
⃗
3*\vec{i} +2*\vec{j}
3∗i+2∗j
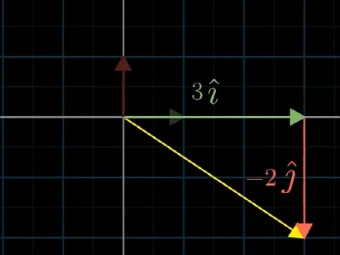
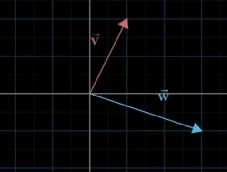
这里需要注意,前面我们选择指向x,y轴,且长度为1的向量作为基向量,但也可以选择不同的基,不同的基代表不同的坐标系,则对于一个向量而言,它代表不同的几何意义,例如,选择下面的v和w向量作为基向量时,向量
[
1.5
−
0.62
]
\begin{bmatrix} 1.5\\ -0.62 \end{bmatrix}
[1.5−0.62]代表的几何形状与
i
⃗
\vec{i}
i,
j
⃗
\vec{j}
j为基向量时的形状是不一样的。
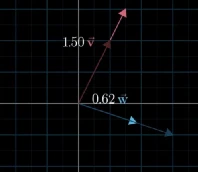
向量线性组合:
无论选择什么样的基向量,向量都可以写成更一般的形式:
a
v
⃗
+
b
w
⃗
a\vec{v} +b\vec{w}
av+bw我们称为向量的线性组合,a,b是标量,也称为缩放因子,v和w是向量,选择不同的缩放因子,向量的线性组合可以表示整个向量空间,也就是生成的向量可以到达平面中所有点。
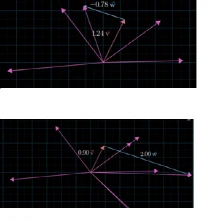
但如果两个向量恰好共线时,则向量组合后的结果向量只能落在该直线上,我们称共线的两个向量是线性相关的,否则是线性无关。
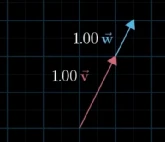
更特殊地,当这两个向量都是0向量时,则向量组合后的结果向量只能落在原点上。
概括一下,所有可以被给定向量,用线性组合来表示的那些向量的集合,被称为给定向量张成的空间,两个不共线的向量,在二维空间中,其线性组合所张成的空间是整个二维空间;而在三维空间中,其张成的空间是三维空间中的一个面。
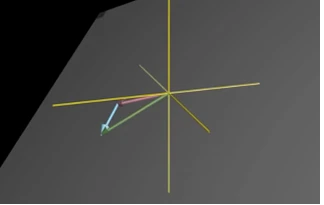
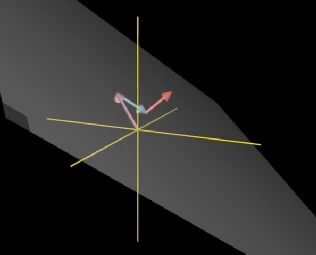
在三维空间中,三个向量的线性组合,如果其中一个向量在另两个向量张成的平面内,我们称该向量与其他两个向量线性相关,这三个向量的线性组合仍然是一个平面,只有三个向量互不线性相关时,那么这三个向量的线性组合才能张成整个三维空间。
矩阵与线性相关
矩阵:
先说结论:前面讲的向量可以视为一种带箭头的几何结构,那么矩阵就可以视为一种对几何的变换。
在线性代数中,变换是一种函数,将输入映射成输出,输入是向量,输出也是向量,同理,当输入是矩阵时,可以把矩阵分解成多个向量,那么输出也就是矩阵,变换有很多种,线性代数中只讨论线性变换,线性变换要求,任意直线变换后仍然是直线,且原点位置变换后保持不变,从几何角度看,线性变换就是拉伸,缩放,旋转。
下图变换后,直线变弯曲了,所以是非线性变换
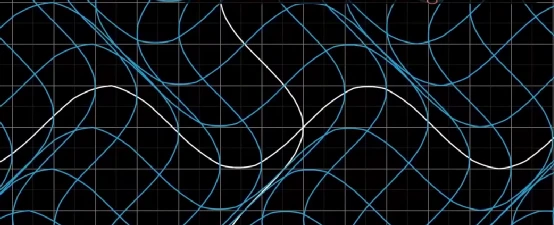
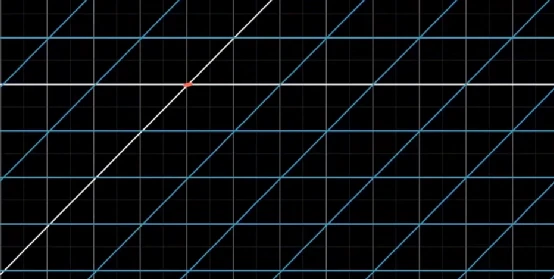
下图变换后,原点位置变了,所以属于非线性变换
那我们如何求一个向量经过变换后的向量坐标呢?假设现有一个向量,在原始坐标系下可以表示成:
v
⃗
=
(
−
1
)
i
⃗
+
2
∗
j
⃗
\vec{v} =( -1)\vec{i} +2*\vec{j}
v=(−1)i+2∗j 。
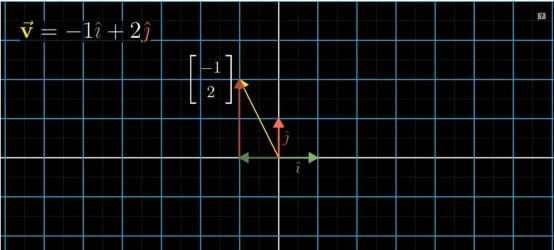
现在对向量v施加一个线性变换,根据线性变换的特性,变换后,网格仍然平行且间隔均等,假设两个基向量变换后的坐标如下图所示,向量v与两个基向量经过相同的变换变成新的基向量,那么,向量v经过变换后的向量仍然可以表示成:
v
⃗
t
r
a
n
s
f
o
r
m
e
d
=
(
−
1
)
i
⃗
t
r
a
n
s
f
o
r
m
e
d
+
2
∗
j
t
r
a
n
s
f
o
r
m
e
d
\begin{equation*} \vec{v}{}_{transformed} =( -1)\vec{i}{}_{transformed} +2*j{}_{transformed} \end{equation*}
vtransformed=(−1)itransformed+2∗jtransformed
只不过基向量变成了变换后的基向量。
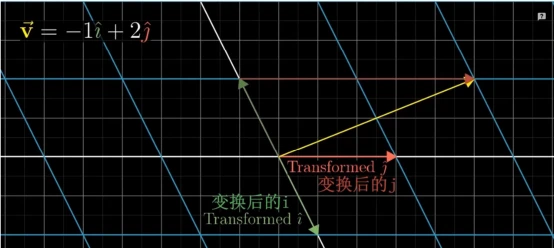
如上图
i
⃗
t
r
a
n
s
f
o
r
m
e
d
=
[
1
−
2
]
\vec{i}{}_{transformed} =\begin{bmatrix} 1\\ -2 \end{bmatrix}
itransformed=[1−2],
j
⃗
t
r
a
n
s
f
o
r
m
e
d
=
[
3
0
]
\vec{j}{}_{transformed} =\begin{bmatrix} 3\\ 0 \end{bmatrix}
jtransformed=[30]
变换后的v就等于: v ⃗ = ( − 1 ) [ 1 − 2 ] + 2 ∗ [ 3 0 ] = [ 5 2 ] \vec{v} =( -1)\begin{bmatrix} 1\\ -2 \end{bmatrix} +2*\begin{bmatrix} 3\\ 0 \end{bmatrix} =\begin{bmatrix} 5\\ 2 \end{bmatrix} v=(−1)[1−2]+2∗[30]=[52]
也就是说,如果我们知道两个基向量变换后的向量,那么求任何一个向量经过变换后的向量的过程可以用下图所表示:
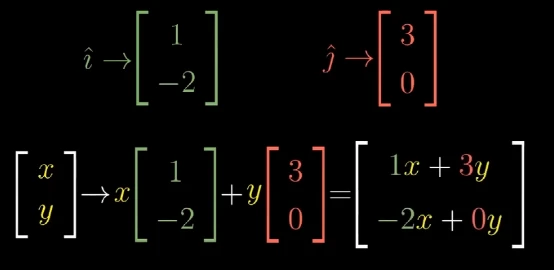
更进一步的,我们将两个基向量变换后的坐标向量用矩阵的形式组织起来,这个矩阵就是线性变换矩阵T。
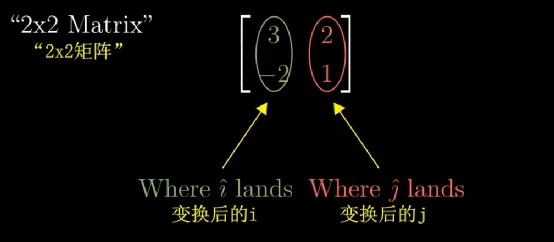
对于任意一个向量A,例如, [ 7 2 ] \begin{bmatrix} 7\\ 2 \end{bmatrix} [72],求该线性变换T对该向量的作用时,只需要用矩阵与向量相乘即可: A t r a n s f o r m e d = [ 3 2 − 2 1 ] [ 7 2 ] = 7 [ 3 − 2 ] + 2 [ 2 1 ] A_{transformed} =\begin{bmatrix} 3 & 2\\ -2 & 1 \end{bmatrix}\begin{bmatrix} 7\\ 2 \end{bmatrix} =7\begin{bmatrix} 3\\ -2 \end{bmatrix} +2\begin{bmatrix} 2\\ 1 \end{bmatrix} Atransformed=[3−221][72]=7[3−2]+2[21]。
如果换个视角,反过来看,如果给出一个矩阵乘法:
[
3
2
−
2
1
]
[
7
2
]
\begin{bmatrix} 3 & 2\\ -2 & 1 \end{bmatrix}\begin{bmatrix} 7\\ 2 \end{bmatrix}
[3−221][72],我们可以把矩阵第一列
[
3
−
2
]
\begin{bmatrix} 3\\ -2 \end{bmatrix}
[3−2]当作新的基向量
i
⃗
\vec{i}
i,把矩阵的第二列
[
2
1
]
\begin{bmatrix} 2\\ 1 \end{bmatrix}
[21]当作新的基向量
j
⃗
\vec{j}
j,根据向量的几何表示,向量
[
7
2
]
\begin{bmatrix} 7\\ 2 \end{bmatrix}
[72]用新的基向量表成:
i
⃗
\vec{i}
i向正方向放大7倍,
j
⃗
\vec{j}
j向正方向放大2倍,将变换后的向量相加就形成了结果向量。

再举个例子,看看逆时针旋转90度的变换矩阵是什么, i ⃗ \vec{i} i由 [ 1 0 ] \begin{bmatrix} 1\\ 0 \end{bmatrix} [10]变成 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01], j ⃗ \vec{j} j由 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01]变成 [ − 1 0 ] \begin{bmatrix} -1\\ 0 \end{bmatrix} [−10],所以该变换矩阵为: [ 0 − 1 1 0 ] \begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix} [01−10]。
到此,就已经证明了我们在开头所说的:矩阵是一种线性变换。