文章目录
- 一次双绝对值不等式求解步骤
- 去绝对值情况分析👺
- 例
- 例
- 代数法
- 几何方法
- 比较
- 例
一次双绝对值不等式求解步骤
-
设 f = ∣ f 1 ∣ + ∣ f 2 ∣ f=|f_1|+|f_2| f=∣f1∣+∣f2∣, f 1 , f 2 f_1,f_2 f1,f2都是一次多项式,则原不等式 f ⩾ a f\geqslant{a} f⩾a或 f ⩽ a f\leqslant{a} f⩽a的解法的一般步骤:划分区间分段并去绝对值号,具体如下(为了称呼方便,用 δ ( f ) \delta(f) δ(f)表示 f ⩾ a f\geqslant{a} f⩾a或 f ⩽ a f\leqslant{a} f⩽a的中的一种)
- 令每个绝对值符号例的一次式 f i = 0 , i = 1 , 2 f_i=0,i=1,2 fi=0,i=1,2为0,求出相应的根 x 1 , x 2 x_1,x_2 x1,x2
- 将这些根排序,设 x 1 < x 2 x_1<x_2 x1<x2,根据 x 1 , x 2 x_1,x_2 x1,x2将实数轴分为若干个区间: ( − ∞ , x 1 ) , ( x 1 , x 2 ) , ( x 2 , + ∞ ) (-\infin,x_1),(x_1,x_2),(x_2,+\infin) (−∞,x1),(x1,x2),(x2,+∞),分别记为 A 1 , A 2 , A 3 A_1,A_2,A_3 A1,A2,A3
- 在各区间上,去掉
f
f
f的绝对值号,将
f
f
f在3个区间内的解析式记为
t
i
,
i
=
1
,
2
,
3
t_i,i=1,2,3
ti,i=1,2,3,分别讨论各个区间内关于原不等式的解集
B
i
,
i
=
1
,
2
,
3
B_i,i=1,2,3
Bi,i=1,2,3;然后取
S
i
=
A
i
∩
B
i
S_i=A_i\cap{B_i}
Si=Ai∩Bi,
i
=
1
,
2
,
3
i=1,2,3
i=1,2,3作为第
i
i
i区间原不等式解集;
Note:不要直接把 B i B_i Bi当作原不等式在第 i i i区间的解集(除非 B i = ∅ B_i=\varnothing Bi=∅), S i S_i Si只是 δ ( t i ) \delta(t_i) δ(ti)在第 i i i区间下表达式的自然解,需要结合第 i i i区间的范围约束才是 δ ( f ) \delta(f) δ(f)的解 - 将各个解集 S i S_i Si作并集, S = ⋃ i = 1 S i S=\bigcup_{i=1}S_i S=⋃i=1Si就得到原不等式解集
-
上述解法可以结合图形法理解,在同一个坐标系中绘制 ∣ f 1 ∣ , ∣ f 2 ∣ |f_1|,|f_2| ∣f1∣,∣f2∣的图形,可以看到三个区间内 f = ∣ f 1 ∣ + ∣ f 2 ∣ f=|f_1|+|f_2| f=∣f1∣+∣f2∣有不同的解析式(不带绝对值号)
-
最后,可以将函数 f f f绘制成分段函数
去绝对值情况分析👺
- 双绝对值的分段化有四种可能的解析式情况(以两个绝对值表达式内部的取值情况为分类标准)
(+,+)(+,-)(-,+)(-,-)
- 可见,采用分类讨论的策略来去掉一次双绝对值函数中的两对绝对值号,最多可以得到4个不同的一次函数,但是实际可以确定2,3两种情况只有一种会发生,分析如下:
- 一次函数 f ( x ) = a x + b , a ≠ 0 f(x)=ax+b,a\neq0 f(x)=ax+b,a=0,( f ( x ) f(x) f(x)不是常数)的绝对值函数 ∣ f ( x ) ∣ |f(x)| ∣f(x)∣可以分为两段, ( − ∞ , − b a ] (-\infin,-\frac{b}{a}] (−∞,−ab]以及 [ − b a , + ∞ ) [-\frac{b}{a},+\infin) [−ab,+∞)
- 对于 f ( x ) = ∣ f 1 ( x ) ∣ + ∣ f 2 ( x ) ∣ f(x)=|f_1(x)|+|f_2(x)| f(x)=∣f1(x)∣+∣f2(x)∣,(其中 f i ( x ) f_i(x) fi(x)都是一次函数);将 ∣ f 1 ( x ) ∣ , ∣ f 2 ( x ) ∣ |f_1(x)|,|f_2(x)| ∣f1(x)∣,∣f2(x)∣的图形绘制在同一个坐标系中
- 记 f i ( x ) f_i(x) fi(x)的根 x i = − b i a i , i = 1 , 2 x_i=-\frac{b_i}{a_i},i=1,2 xi=−aibi,i=1,2,不妨设 x 1 < x 2 x_1<x_2 x1<x2(如果不是则调换 ∣ f 1 ( x ) ∣ , ∣ f 2 ( x ) ∣ |f_1(x)|,|f_2(x)| ∣f1(x)∣,∣f2(x)∣,因为加法满足交换律),当 x < x 1 x<x_1 x<x1; x 1 ⩽ x ⩽ x 2 x_1\leqslant{x}\leqslant{x_2} x1⩽x⩽x2以及 x > x 2 x>x_2 x>x2时 ∣ f 1 ( x ) ∣ , ∣ f 2 ( x ) ∣ |f_1(x)|,|f_2(x)| ∣f1(x)∣,∣f2(x)∣在各自区间内的去绝对值后的解析式之和不发生改变
- 可见,只需要分3个区间段就可以完成对 f ( x ) f(x) f(x)的分段分析(去绝对值分析),且3个区间段由 f 1 ( x ) , f 2 ( x ) f_1(x),f_2(x) f1(x),f2(x)的根确定
例
- 设 f ( x ) = ∣ x − 1 ∣ + ∣ x − 2 ∣ f(x)=|x-1|+|x-2| f(x)=∣x−1∣+∣x−2∣,求 f ( x ) > 5 f(x)>5 f(x)>5的解集
- 解:
- 计算两个一次式的根: x 1 = 1 x_1=1 x1=1, x 2 = 2 x_2=2 x2=2
- x ∈ ( − ∞ , 1 ] x\in(-\infin,1] x∈(−∞,1], f ( x ) = t 1 ( x ) = 1 − x + 2 − x = − 2 x + 3 f(x)=t_1(x)=1-x+2-x=-2x+3 f(x)=t1(x)=1−x+2−x=−2x+3,此时 t 1 ( x ) > 5 t_1(x)>5 t1(x)>5的解集为 x < − 1 x<-1 x<−1,此时 f ( x ) > 5 f(x)>5 f(x)>5的解集为: ( − ∞ , 1 ] ∩ ( − ∞ , − 1 ) (-\infin,1]\cap(-\infin,-1) (−∞,1]∩(−∞,−1)= ( − ∞ , − 1 ) (-\infin,-1) (−∞,−1)
- x ∈ ( 1 , 2 ) x\in(1,2) x∈(1,2), f ( x ) = t 2 ( x ) = x − 1 + 2 − x = 1 f(x)=t_2(x)=x-1+2-x=1 f(x)=t2(x)=x−1+2−x=1, t 2 ( x ) > 5 t_2(x)>5 t2(x)>5的解集为 ∅ \varnothing ∅,此时 f ( x ) > 5 f(x)>5 f(x)>5的解集为: ∅ \varnothing ∅
- x ∈ [ 2 , + ∞ ) x\in[2,+\infin) x∈[2,+∞), f ( x ) = t 3 ( x ) = x − 1 + x − 2 = 2 x − 3 f(x)=t_3(x)=x-1+x-2=2x-3 f(x)=t3(x)=x−1+x−2=2x−3, t 3 ( x ) > 5 t_3(x)>5 t3(x)>5的解集为 x > 4 x>4 x>4,此时 f ( x ) > 5 f(x)>5 f(x)>5的解集为 ( 4 , ∞ ) (4,\infin) (4,∞)
- 综上, f ( x ) > 5 f(x)>5 f(x)>5的解集为 ( − ∞ , − 1 ) ∪ ∅ ∪ ( 4 , ∞ ) (-\infin,-1)\cup{\varnothing}\cup{(4,\infin)} (−∞,−1)∪∅∪(4,∞)= ( − ∞ , − 1 ) ∪ ( 4 , ∞ ) (-\infin,-1)\cup{(4,\infin)} (−∞,−1)∪(4,∞)
例
- 本例主要演示分区间内去绝对值的推荐做法以及几何方法求解
代数法
-
设 f ( x ) = ∣ x + 2 ∣ + ∣ x − 1 ∣ f(x)=|x+2|+|x-1| f(x)=∣x+2∣+∣x−1∣,求 f ( x ) < 4 f(x)<4 f(x)<4
-
求区间划分点: x 1 = − 2 , x 2 = 1 x_1=-2,x_2=1 x1=−2,x2=1
-
x ⩽ − 2 x\leqslant{-2} x⩽−2时
- x + 2 ⩽ − 2 + 2 = 0 x+2\leqslant{-2+2=0} x+2⩽−2+2=0
- x − 1 ⩽ − 3 − 1 = − 4 ⩽ 0 x-1\leqslant{-3-1}=-4\leqslant{0} x−1⩽−3−1=−4⩽0
- f ( x ) = − x − 2 − x + 1 = − 2 x − 1 f(x)=-x-2-x+1=-2x-1 f(x)=−x−2−x+1=−2x−1
- 此时 f ( x ) < 4 f(x)<4 f(x)<4的解集为 ( − ∞ , − 2 ] ∩ ( − 5 2 , + ∞ ) (-\infin,-2]\cap (-\frac{5}{2},+\infin) (−∞,−2]∩(−25,+∞),即 ( − 5 2 , − 2 ] (-\frac{5}{2},-2] (−25,−2]
-
− 2 < x < 1 -2<x<1 −2<x<1
- 0 < x + 2 < 3 0<x+2<3 0<x+2<3
- − 3 < x − 1 < 0 -3<x-1<0 −3<x−1<0
- f ( x ) = x + 2 − x + 1 = 3 f(x)=x+2-x+1=3 f(x)=x+2−x+1=3
- 此时 f ( x ) < 4 f(x)<4 f(x)<4的解集为 ( − 2 , 1 ) (-2,1) (−2,1)
-
x ⩾ 1 x\geqslant{1} x⩾1
- x + 2 ⩾ 1 x+2\geqslant{1} x+2⩾1
- x − 1 ⩾ 0 x-1\geqslant{0} x−1⩾0
- f ( x ) = x + 2 + x − 1 = 2 x + 1 f(x)=x+2+x-1=2x+1 f(x)=x+2+x−1=2x+1
- 此时 f ( x ) < 4 f(x)<4 f(x)<4的解集为 [ 1 , + ∞ ) ∩ ( − ∞ , 3 2 ) [1,+\infin)\cap(-\infin,\frac{3}{2}) [1,+∞)∩(−∞,23)= [ 1 , 3 2 ) [1,\frac{3}{2}) [1,23)
-
综上,原不等式 f ( x ) < 4 f(x)<4 f(x)<4的解集为 ( − 5 2 , − 2 ] ∪ ( − 2 , 1 ) ∪ [ 1 , 3 2 ) (-\frac{5}{2},-2]\cup(-2,1)\cup[1,\frac{3}{2}) (−25,−2]∪(−2,1)∪[1,23)= ( − 5 2 , 3 2 ) (-\frac{5}{2},\frac{3}{2}) (−25,23)
-
几何方法
- x x x为不等式 ∣ x + 2 ∣ + ∣ x − 1 ∣ = ∣ x − ( − 2 ) ∣ + ∣ x − 1 ∣ < 4 |x+2|+|x-1|=|x-(-2)|+|x-1|<4 ∣x+2∣+∣x−1∣=∣x−(−2)∣+∣x−1∣<4 ⇔ \Leftrightarrow ⇔ x x x是数轴上的点 A ( − 2 ) A(-2) A(−2)和 B ( 1 ) B(1) B(1)两点距离之和小于4的点
- 记 ∣ A B ∣ |AB| ∣AB∣表示 A , B A,B A,B的距离, f ( x ) = ∣ A X ∣ + ∣ B X ∣ f(x)=|AX|+|BX| f(x)=∣AX∣+∣BX∣
- ∣ A B ∣ = ∣ − 2 − 1 ∣ = 3 |AB|=|-2-1|=3 ∣AB∣=∣−2−1∣=3,因此 f ( x ) = 3 < 4 f(x)=3<4 f(x)=3<4,可见 x ∈ [ − 2 , 1 ] x\in[-2,1] x∈[−2,1]是 f ( x ) < 4 f(x)<4 f(x)<4的解
- 为了找到全部解,考虑在
A
,
B
A,B
A,B之外的点
- 若 X X X在距离A左侧 δ ( δ > 0 ) \delta(\delta>0) δ(δ>0)处,则 f ( x ) = ∣ A B ∣ + 2 δ = 3 + 2 δ f(x)=|AB|+2\delta=3+2\delta f(x)=∣AB∣+2δ=3+2δ,因此, f ( x ) < 4 f(x)<4 f(x)<4 ⇔ \Leftrightarrow ⇔ δ < 1 2 \delta<\frac{1}{2} δ<21,将临界点记为 A ′ = − 2 − δ = − 5 2 A'=-2-\delta=-\frac{5}{2} A′=−2−δ=−25
- 若 X X X在距离 B B B右侧 ϕ ( ϕ > 0 ) \phi(\phi>0) ϕ(ϕ>0)处,类似的有 ϕ < 1 2 \phi<\frac{1}{2} ϕ<21,将临界点记为 B ′ = 1 + 1 2 = 3 2 B'=1+\frac{1}{2}=\frac{3}{2} B′=1+21=23
- 因此 f ( x ) < 4 f(x)<4 f(x)<4的解集为 A ′ B ′ A'B' A′B′内的点,即 ( − 5 2 , 3 2 ) (-\frac{5}{2},\frac{3}{2}) (−25,23)
比较
- 几何方法的局限性在于仅对 ∣ x + b ∣ + ∣ x + c ∣ |x+b|+|x+c| ∣x+b∣+∣x+c∣型的比较方便,否则使用更通用的代数法求解,重点是分类讨论
例
-
已知函数 f ( x ) = ∣ x + 1 ∣ − ∣ 2 x − 3 ∣ f(x)=|x+1|-|2x-3| f(x)=∣x+1∣−∣2x−3∣,求不等式 ∣ f ( x ) ∣ > 1 |f(x)|>1 ∣f(x)∣>1的解集
-
令 f 1 ( x ) = x + 1 ; f 2 ( x ) = 2 x − 3 f_1(x)=x+1;f_2(x)=2x-3 f1(x)=x+1;f2(x)=2x−3则 f ( x ) = ∣ f 1 ( x ) ∣ + ∣ f 2 ( x ) ∣ f(x)=|f_1(x)|+|f_2(x)| f(x)=∣f1(x)∣+∣f2(x)∣
-
(1):
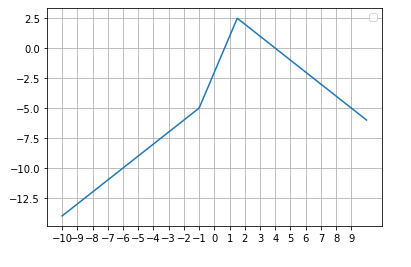
- f ( x ) = { x − 4 , ( − ∞ , − 1 ] 3 x − 2 , ( − 1 , 3 2 ) − x + 4 , [ 3 2 , + ∞ ) f(x)= \begin{cases} x-4,&(-\infin,-1]\\ 3x-2,&(-1,\frac{3}{2}) \\ -x+4,&[\frac{3}{2},+\infin) \end{cases} f(x)=⎩ ⎨ ⎧x−4,3x−2,−x+4,(−∞,−1](−1,23)[23,+∞)
-
(2):
-
先将原不等式去绝对值
-
∣ f ( x ) ∣ > 1 ⇔ { f ( x ) > 1 f ( x ) < − 1 |f(x)|>1 \Leftrightarrow{ \begin{cases} f(x)>1\\ f(x)<-1 \end{cases} } ∣f(x)∣>1⇔{f(x)>1f(x)<−1
-
方法1:结合(1)分段函数的图形
-
方法2:
-
f ( x ) > 1 f(x)>1 f(x)>1
- x − 4 > 1 x-4>1 x−4>1, x ∈ ( 5 , + ∞ ) x\in(5,+\infin) x∈(5,+∞), ( 5 , + ∞ ) ∩ ( − ∞ , − 1 ] = ∅ (5,+\infin)\cap{(-\infin,-1]}=\empty (5,+∞)∩(−∞,−1]=∅
- 3 x − 2 > 1 3x-2>1 3x−2>1, x ∈ ( 1 , + ∞ ) x\in(1,+\infin) x∈(1,+∞), ( − 1 , 3 2 ) ∩ ( 1 , + ∞ ) (-1,\frac{3}{2})\cap{(1,+\infin)} (−1,23)∩(1,+∞)= ( 1 , 3 2 ) (1,\frac{3}{2}) (1,23)
- − x + 4 > 1 -x+4>1 −x+4>1, x ∈ ( − ∞ , 3 ) x\in(-\infin,3) x∈(−∞,3), [ 3 2 , + ∞ ) ∩ ( − ∞ , 3 ) [\frac{3}{2},+\infin)\cap{(-\infin,3)} [23,+∞)∩(−∞,3)= [ 3 2 , 3 ) [\frac{3}{2},3) [23,3)
-
f ( x ) < − 1 f(x)<-1 f(x)<−1
- x − 4 < − 1 x-4<-1 x−4<−1, x ∈ ( − ∞ , − 1 ] x\in(-\infin,-1] x∈(−∞,−1]
- 3 x − 2 < − 1 3x-2<-1 3x−2<−1, x ∈ [ − 1 , 1 3 ) x\in[-1,\frac{1}{3}) x∈[−1,31)
- − x + 4 < − 1 -x+4<-1 −x+4<−1, x ∈ ( 5 , + ∞ ) x\in(5,+\infin) x∈(5,+∞)
-
将上述6个几何求并集,得到 ∣ f ( x ) ∣ > 1 |f(x)|>1 ∣f(x)∣>1的解集: ( − ∞ , − 1 3 ) (-\infin,-\frac{1}{3}) (−∞,−31) ∪ \cup ∪ ( 1 , 3 ) (1,3) (1,3) ∪ \cup ∪ ( 5 , + ∞ ) (5,+\infin) (5,+∞)
-
-



![【PWN · heap | unlink | free_hook】[SUCTF 2018 招新赛]unlink](https://img-blog.csdnimg.cn/9d2f14d0796b46b28facb9ce7594bf61.png)