分类目录：《深入理解强化学习》总目录

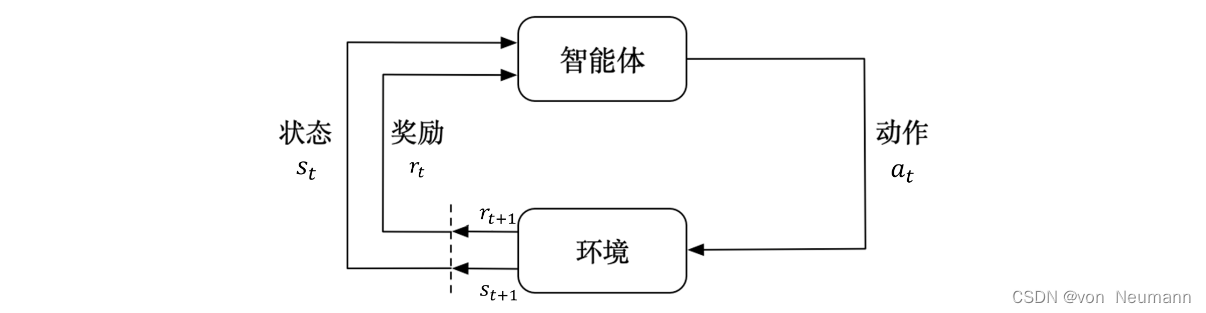
下图介绍了强化学习里面智能体与环境之间的交互，智能体得到环境的状态后，它会采取动作，并把这个采取的动作返还给环境。环境得到智能体的动作后，它会进入下一个状态，把下一个状态传给智能体。在强化学习中，智能体与环境就是这样进行交互的，这个交互过程可以通过马尔可夫决策过程来表示，所以马尔可夫决策过程是强化学习的基本框架。

《深入理解强化学习——马尔可夫过程》系列文章将介绍马尔可夫决策过程。与多臂老虎机问题不同，马尔可夫决策过程包含状态信息以及状态之间的转移机制。如果要用强化学习去解决一个实际问题，第一步要做的事情就是把这个实际问题抽象为一个马尔可夫决策过程，也就是明确马尔可夫决策过程的各个组成要素。在介绍马尔可夫决策过程之前，我们将先介绍它的简化版本：马尔可夫过程（Markov Process，MP）以及马尔可夫奖励过程（Markov Reward Process，MRP）。通过与这两种过程的比较，我们可以更容易理解马尔可夫决策过程。其次，我们会介绍马尔可夫决策过程中的策略评估（Policy Evaluation），就是当给定决策后，我们怎么去计算它的价值函数。最后，我们会介绍马尔可夫决策过程的控制，具体有策略迭代（Policy Iteration） 和价值迭代（Value Iteration）两种算法。在马尔可夫决策过程中，它的环境是全部可观测的。但是很多时候环境里面有些量是不可观测的，但是这个部分观测的问题也可以转换成马尔可夫决策过程的问题。

随机过程

随机过程（Stochastic Process）是概率论的“动力学”部分。概率论的研究对象是静态的随机现象，而随机过程的研究对象是随时间演变的随机现象（例如天气随时间的变化、城市交通随时间的变化）。在随机过程中，随机现象在某时刻$t$的取值是一个向量随机变量，用$S_t$表示，所有可能的状态组成状态集合$S$。随机现象便是状态的变化过程。在某时刻$t$的状态$S_t$通常取决于$t$时刻之前的状态。我们将已知历史信息$(S_1,S_2,\cdots ,S_t)$时下一个时刻状态$S_{t+1}$为的概率表示成$P(S_{t+1}|S_1,S_2,\cdots ,S_t)$。

马尔可夫性质

当且仅当某时刻的状态只取决于上一时刻的状态时，一个随机过程被称为具有马尔可夫性质（Markov Property），用公式表示为$P(S_{t+1}|S_t)=P(S_{t+1}|S_1,S_2,\cdots ,S_t)$。也就是说，当前状态是未来的充分统计量，即下一个状态只取决于当前状态，而不会受到过去状态的影响。需要明确的是，具有马尔可夫性并不代表这个随机过程就和历史完全没有关系。因为虽然时刻$t+1$的状态只与时刻$t$的状态有关，但是时刻的$t$状态其实包含了时刻$t-1$的状态的信息，通过这种链式的关系，历史的信息被传递到了现在。马尔可夫性可以大大简化运算，因为只要当前状态可知，所有的历史信息都不再需要了，利用当前状态信息就可以决定未来。

参考文献：
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习（第2版）[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践（原书第2版）[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL：强化学习教程 [M]. 人民邮电出版社, 2022