Monarch Mixer: A Simple Sub-Quadratic GEMM-Based Architecture

news2024/10/7 16:17:22

Monarch Mixer: A Simple Sub-Quadratic GEMM-Based Architecture

发于 2023年AI顶会 NeurIPS。

sub-quadratic primitive(次二次原语)

GEMMs（General Matrix Multiply algorithms）是指在许多核心系统上执行的通用矩阵乘法操作的模型。

“causal model”（因果模型）和 “non-causal model”（非因果模型）之间的区别。

Causal model（因果模型）是一种建模方法，旨在理解因果关系和因果推断。这种模型试图描述变量之间的因果关系，即某个变量的变化如何导致其他变量的变化。因果模型通常基于因果关系图，其中节点表示变量，边表示因果关系。

Causal model的一个重要特征是它能够根据因果关系进行因果推断。例如，如果有一个因果模型描述了药物治疗和疾病之间的关系，我们可以使用该模型来预测给定某种治疗方案的情况下，患者的疾病状况会如何改变。

Non-causal model（非因果模型）则不涉及因果关系的建模。这些模型可能只是对数据进行描述、预测或分类，而不考虑变量之间的因果关系。非因果模型可以是统计模型、机器学习模型或其他描述性模型。

FFT(快速傅里叶变换)

在这里插入图片描述

摘要

现在大多数的工作为了提示模型在长文本的表现，都是想办法去缩减序列的长度和模型的维度来实现。
作者提出来了一种新的模型 **Monarch Mixer（M2）**一种新的模型，uses the same sub-quadratic primitive(用相同的次二次原语)。
Monarch矩阵(也是新突出的概念)，一类简单的表达型结构化矩阵，可以捕获许多线性变换，在GPU上实现高硬件效率，并按次二次方进行扩展。
为了证明其效果，作者在：
1、non-causal BERT-style language modeling
2、ViT-style image classification
3、causal GPT-style language modeling
三个任务上做了实验。
最后的结果都是可以省掉一大半参数资源的情况下，达到和模型相似甚至更高的模型结果。

Introduction

作者想在序列长度和模型维度上面都找到二次型的运算原语。框架灵感来自于 MLP-mixer和ConvMixer。
Monarch: Expressive structured matrices for efficient and accurate training是基于这篇文章的Monarch做的更改。

在这里插入图片描述
👆解释了Monarch的优越性。

Preliminaries

GPU Accelerator Cost Model

讨论GPU加速的问题，可以把GPU的计算操作分为compute-bound(计算绑定)和memory-bound(内存绑定)。
这里memory-bound(内存绑定)的计算相对于arithmetic 操作微乎其微，例子：Typical examples are matrix multiply with large inner
dimension, and short convolution kernels with a large number of channels.(典型的例子是具有大内维数的矩阵乘法和具有大量通道的短卷积核)。
GPU计算方面结论：matrix multiply operation比non-matrix multiply operations(没有矩阵综合运算)的快15倍左右。
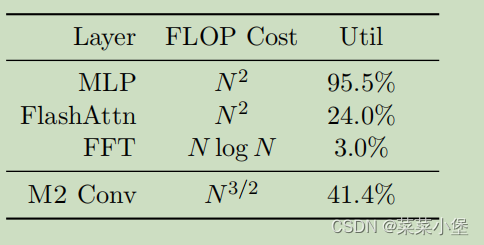
在这里插入图片描述